Programação Dinâmica I
Este é o primeiro de uma série de posts que eu pretendo fazer sobre um tema interessante, complicado e que usa programação pesadamente - o que faz dele um carro chefe para a proposta desse blog: programação dinâmica. O nome engana: apesar de usarmos ferramentas computacionais para resolver o problema, a programação dinâmica trata de problemas de otimização no tempo. O nosso objetivo final vai ser resolver um problema de um agente otimizando a sua utilidade no tempo sem uma data final - o tempo vai para o infinito - sujeito à alguma restrição de recursos. Formalmente, o problema é:
\[ \max_{c} \sum_{t=1}^\infty \beta^{t}u(c_t) \text{ sujeito a } c_t = f(k_t)\]
Onde \(u()\) é uma função utilidade, \(\beta\) é uma taxa de desconto. A variável \(c\) é conhecida como variável de controle e a variável \(k\) é a variável de estado. Ou seja, escolhemos um valor de \(c\) (por isso controle) e isso define a variável \(k\). Eu usei as letras \(c\) e \(k\) de propósito para sugerir que o agente escolhe o consumo e isso impacta em um valor do capital amanhã. Nesse caso, a restrição seria da forma:
\[k_{t+1} = (1-\delta)k_t+I_t\]
Onde \(\delta\) representa a taxa de depreciação e \(I_t\) representa o investimento feito. Esta restrição é chama de lei de movimento, porque descreve como o capital se “movimenta” no tempo. Também temos uma função de produção \(y(k_t)\), que vamos supor que é Cobb Douglas com paramêtro \(\alpha\). Em um caso sem governo, toda a produção vai ser dividida entre investimento e consumo, então podemos rescrever a equação acima como:
\[k_{t+1} + c_t = (1-\delta)k_t+y(k_t)\]
Se você precisa de algum convencimento sobre por que aprender a resolver um problema que vai “para o infinito”, dado que nós temos uma vida finita, pense que isso pode ser uma boa aproximação da realidade por dois motivos: primeiro, porque para alguém entrando no mercado de trabalho agora e com uma expectativa de vida de 80 anos, mais 60 anos é “infinito”. Nós não sabemos quando vamos morrer exatamente, então colocar uma data T fixa parece um pouco arbitrário: o agente saberia exatamente quando a vida dele ia acabar, e isso parece mais irrealista que um problema “no infinito”. Essa também é uma maneira suja, mas simples, de introduzir altruísmo: o agente não otimiza com relação a si mesmo, mas sim pensando em todas as gerações futuras.
Existem várias maneiras de abordar o problema de programação dinâmica, e o assunto pode ficar altamente matemático rapidamente. Uma maneira “padrão” de resolver é escrever o problema acima como um lagrangeano padrão e tirar a derivada em relação a variável de controle no tempo \(t\), \(k_{t+1}\). Para este caso, podemos reescrever a restrição para isolar o \(c_t\) e substituir no problema. Com isso, temos:
\[\sum_{t=1}^\infty u((1-\delta)k_t+y(k_t)-k_{t+1})\]
Veja que o \(k_{t+1}\) aparece duas vezes no somatório: no período \(t\), subtraindo e no período \(t+1\) nos termos \(k_t\) (se você está achando confuso, abra o somatório para \(t\) e \(t+1\) e ignore o resto dos termos). Podemos tirar a derivada com relação a \(k_{t+1}\) obteríamos a condição de primeira ordem:
\[-\beta^{t}u^{\prime}(c_{t}) + \beta^{t+1}u^{\prime}(c_{t+1})[(1-\delta)+y^{\prime}(k_{t+1})] = 0\]
A equação acima é o suficiente para o Dynare - que é o padrão para estimar modelos em macroeconomia - resolver o problema. Essa abordagem tem uma qualidade: coloca um problema esquisito em uma roupagem usual. Mas ela esconde o problema de que temos infinitos controles para escolher, e não podemos usar as infinitas condições de primeira ordem para achar uma solução do problema. Vamos usar uma abordagem totalmente diferente, que é a programação dinâmica. Começaremos com um problema mais simples, mas instrutivo: o de horizonte finito.
Um problema com horizonte finito
Vamos supor que no problema anterior, ao invés de termos infinitos períodos, temos um número \(T\) de períodos. Poderíamos resolver usando o lagrangeano usual, mas podemos proceder por um caminho totalmente diferente - e que vai gerar um estranhamento inicial.
Suponha que você se encontra no último período, \(T\). Qual a estratégia ótima? Desconsiderando altruísmo - como de praxe - o ideal é consumir todo o estoque de capital de hoje, \(k_T\). Isso gera uma utilidade \(u(k_T)\). Agora, suponha que você está em \(T-1\). A sua utilidade hoje é o quanto você vai consumir hoje mais o quanto você vai consumir amanhã trazido a valor presente. Quando você escolher o consumo em \(T-1\), você deve levar em consideração tanto a utilidade hoje como o impacto para o capital amanhã. Voltando para o mundo da matemática, vamos chamar o valor máximo disso de \(V_{T-1}\):
\[ V_{T-1}(k_{T-1},c_{T-1}) = \max_{c_{T-1}} u(c_{T-1}) + \beta u(k_T) \]
Veja que o \(k_{T-1}\) aparece implicitamente na função acima, já que precisamos dele para calcular \(k_T\).
E para \(T-2\)? Você vai ter que levar em conta o quanto o seu consumo impacta a utilidade em \(T-2\) e a acumulação de capital - e por tabela a utilidade - em \(T-1\) e \(T\). Mas, convenientemente, a função \(V_{T-1}(k_{T-1},c_{T-1})\) leva em conta o impacto do seu consumo em \(T-2\) nos períodos seguintes, já que ao determinar \(c_{T-2}\) determinamos \(k_{T-1}\), que é essencial para definirmos \(c_{T-1}\). Podemos escrever uma função, \(V_{T-2}\):
\[ V_{T-2}(k_{T-2},c_{T-2}) = \max_{c_{T-2}} u(c_{T-2}) + \beta*V(k_{T-1},c_{T-1}) \]
Se você ainda não entendeu para onde isso está indo, eu pretendo escrever o problema de maximização de uma data \(t\) qualquer como um problema que depende de \(V_{t+1}(k_{t+1},c_{t+1})\). O problema na data \(t\) é:
\[ V_t(k_t,c_t) = \max_{c_t} u(c_t) + \beta V_{t+1}(k_{t+1},c_{t+1}) \]
Eu estou chamando a função de \(V\) porque ela recebe o nome de função valor. Afinal, ela é o valor do problema de otimização. Vale observar que o problema do período \(t\) depende do valor do problema \(t+1\), e por isso chamamos o problema de recursivo.
Toda a historia dos últimos paragráfos tem um problema claro: eu supus que eu sabia o valor do capital em todas as datas, que depende das escolhas de \(c_t\) para cada data. De certa forma, eu estou dizendo que se eu soubesse a solução, eu saberia a solução. Não é exatamente animador.
A boa notícia é que temos uma solução: compute \(V_t\) para vários valores de \(k\) em todos os períodos! Isso é trabalhoso para o computador, mas problema dele. Eis um pseudo código para resolver o problema:
- Estabeleça um grid de valores para \(k\): um vetor que vai de um \(a\) a \(b\). No Julia, o comando que faz isso é
range. - Comece do período \(T\), compute o valor de \(u()\) para todos os valores do grid.
- Para um \(t\), compute resolva o problema de \(V_{t}\) para um dado valor de K. Lembre que isso vai depender do valor do problema no período seguinte, \(V_{t+1}\), que já foi resolvido.
Veja que isso também tem seus problemas: quando escolhermos o \(c_t\) ótimo, nada impede que o \(k_{t+1}\) implicado por ele não esteja no grid. Podemos aumentar a densidade de pontos no grid, mas mesmo isso não é garantia de resolver o problema. Uma solução é interpolar entre os pontos, e eu já tratei disso em outro post. No Julia, o pacote Interpolations faz interpolação e usaremos ele. Vamos colocar 100 períodos e 100 pontos entre \(0.1\) e \(5\) para o grid do capital.
Nesse primeiro exemplo, eu deixei \(\delta = 1\), ou seja, o capital sempre se deprecia totalmente. A grande vantagem desse exemplo é que ele tem solução fechada e a gente pode comparar a solução numérica com a solução analítica:
using Optim
using Interpolations
using Plots
T = 100
alpha = 0.5
bet = 0.98
delt = 1
dens = 100
u(c) = log(c)
f(k) = k^alpha
K = range(0.1,stop = 5,length = dens)
C = Array{Float64}(undef,T,length(K))
V = Array{Float64}(undef,T,length(K))
V[1,1:length(K)] = u.(K)
C[1,1:length(K)] = K
for j = 2:T
valor=LinearInterpolation(K,V[(j-1),1:length(K)],extrapolation_bc= Interpolations.Linear())
for i = 1:length(K)
val(c)=-u(c)-bet*valor((1-delt)*K[i]+f(K[i])-c)
otimo = optimize(val,0.1,K[i])
V[j,i] = -Optim.minimum(otimo)
C[j,i] = Optim.minimizer(otimo)
end
end
Isso vai nos dar a solução para os valores de K entre 0.1 e 5 para todas as 100 datas. A matriz V guarda o valor da função \(V\) e a matriz C guarda o nível ótimo de consumo para cada nível de capital. Da maneira que eu organizei, cada linha recebe o valor de uma data e cada coluna é um ponto do grid. Não há nenhum impedimento para fazer o contrário. Observe que a primeira linha tem a função valor no último período, a segunda linha a função valor no penúltimo etc.
(Uma nota para aqueles que não estão familiarizados com o Julia: x[1,:] pega todos os elementos da primeira linha da matriz x)
Veja ainda que, como de praxe, o comando optimize só procura mínimos, então nós multiplicamos a função por \(-1\) para transformar o máximo em mínimo. Como o que nos interessa é o valor verdadeiro da função - e não o valor na forma de “mínimo” - temos que multiplicar por \(-1\) quando inserimos o valor na matriz \(V\).
Mas nosso interesse é em saber, para um dado valor incial de \(k\), qual deve ser a trajetória ótima de consumo. Vamos escrever outro código, que pega um valor inicial de \(k\), procura o \(c\) ótimo para aquele valor - usando a matriz C acima - e computa o capital do próximo período usando a lei de movimento \(k_{t+1} + c_t = (1-\delta)k_t+y(k_t)\).
start_val = 2
C_path = Array{Float64}(undef,T)
K_path = Array{Float64}(undef,T)
K_path[T] = start_val
K_true = Array{Float64}(undef,T)
K_true[T]=start_val
for j = T:-1:2
func_cons = LinearInterpolation(K,C[j,1:length(K)], extrapolation_bc = Interpolations.Linear())
C_path[j] = func_cons(K_path[j])
K_path[j-1] = f(K_path[j]) - func_cons(K_path[j]) + (1-delt)*K_path[j]
K_true[j-1] = alpha*bet*(1 - (alpha*bet)^(T-(T-j)))/(1-*(alpha*bet)^(T-(T-j-1)))*f(K_true[j])
end
C_path[1] = K_path[1]
Veja que o for não vai até o último período: como o consumo hoje determina o capital amanhã, o consumo de \(T-1\) vai determinar o capital de \(T\), que é consumido em sua totalidade. Vamos plotar isso para ver a trajetória do consumo e do capital:
plot(C_path[(T-5):-1:1], lab = "Consumo")
plot!(K_path[(T-5):-1:1], lab = "Trajetória estimada do Capital")
plot!(K_true[T:-1:10], lab = "Trajetória verdadeira do Capital")
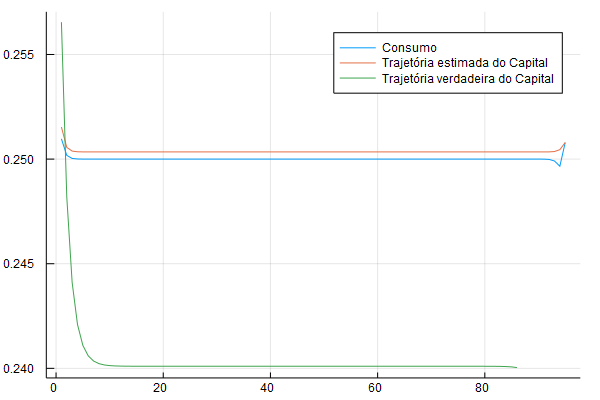
Veja que como a última linha da matriz é na verdade o primeiro período, eu faço gráfico invertendo o vetor, por isso [T:-1:1]: leia isso como “vá de T a 1 com um passo de -1 por vez”.
O gráfico acima é um pouco ruim para ver o quão bom é a aproximação numérica. No gráfico abaixo eu ploto a diferença entre a trajetória analítica e a trajetória estimada numericamente para o problema:
err = K_true[T:-1:1] - K_path[T:-1:1]
plot(err, lab = "Erro na trajetória estimada")
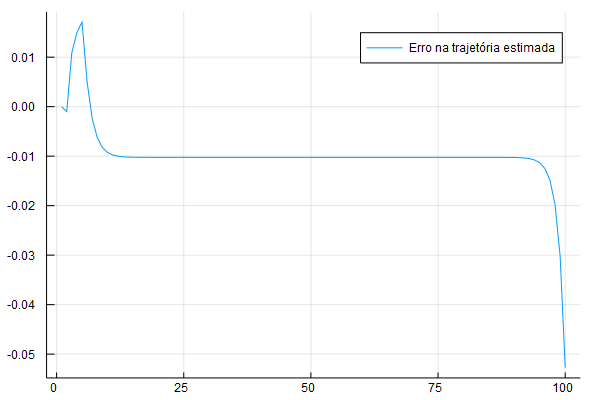
Veja que existe uma pequena diferença inicial e uma diferença grande no final - que explica aquele aumento súbito no consumo: o agente se vê com muito mais capital do que ele gostaria e no último período ele consome tudo. A diferença aqui é de 0.01, o que é relativamente pequeno.
Vamos fazer mais um exemplo, desse vez com capital se depreciando a uma taxa bem menor, 0.3. O código é idêntico ao anterior, mas mudamos para ter delta = 0.3. Essa é a nova cara da trajetória de consumo e capital:
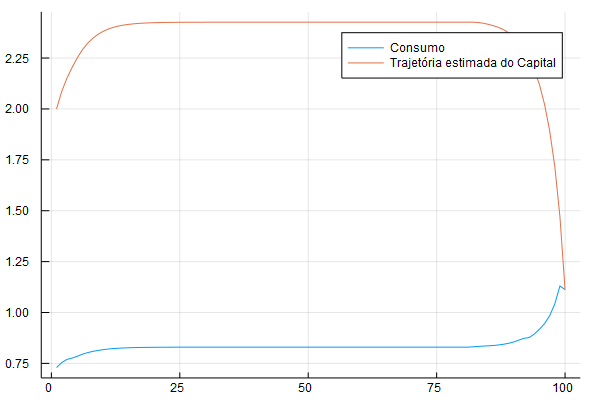
A trajetória faz sentido: o sujeito acumula capital e chegando no fim consome o capital para não sobrar nenhum capital depois de \(T\). Veja que a trajetória do consumo é mais ou menos constante, exceto no fim. É uma manifestação da hipótese de renda permanente, famoso devido a Milton Friedman e Franco Modigliani - uma ideia que eu vou abordar mais nos próximos posts sobre o tema.
Nos próximos posts eu pretendo falar de duas extensões importantes: incerteza e o caso em que o tempo vai para o infinito. Os dois posts serão independentes.
Referências
As referências estão ordenadas em ordem das que eu achei mais útil. A primeira é o quantecon, do Thomas Sargent e John Stachurski. Eles discutem programação dinâmica, fornecem códigos para Julia e Python e discutem um tanto da matemática por trás. Esse post deve muito ao quantEcon. Uma outra referência do Thomas Sargent é o famoso Recursive Macroeconomic Theory. Outra referência muito útil e que inspirou o tratamento desse post é o Economic Dynamic in discrete time, de Jianjun Miao.
Para os leitores interessados na matemática por trás, o Introduction to Modern Economic Growth, do Acemoglu. Outras referências úteis incluem o Economic Dynamics: Theory and Computation, de John Stachurski e Elements of Dynamic Optimization do Chiang.