Sistemas Dinâmicos e Álgebra Linear

Este é mais um post na linha de “como eu gostaria de ter sido apresentado à”. O tema de hoje é Algebra Linear. Este é um dos cursos que muitos alunos acham excessivamente abstrato, e portanto, inútil. De fato, eu tive um pouco desta sensação quando eu fiz o curso. A verdade está muito distante disso.

Suponha que nós temos um sistema de equações (lineares), e este sistema evolui ao longo do tempo. Ele pode ser descrito como \(x_{t+1} = Ax_{t}\), onde \(x_t\) é o vetor de interesse e \(A\) é a matriz que governa como as variáveis se relacionam. Também precisamos de uma condição inicial \(x_0\). Veja que calcular o valor do sistema no tempo \(T\) é equivalente a fazer \(A^{T} x_0\), onde \(A^{T} = A \times A \times A\), \(T\) vezes.

Já encontramos uma situação similar a essa em um post anterior, no qual eu falei de Autoregressão vetorial (VAR). Lá, estavamos interessados em recuperar a matriz A, e o nosso sistema tinha um choque aleatório \(\epsilon_t\). Nosso interesse hoje é saber quando o sistema é estável. Ser estável quer dizer que o sistema não explode, como é o caso do exemplo abaixo:

A <- rbind(c(0.8,0.7),c(0.6,0.7))
x <- matrix(0,ncol = 2, nrow = 100)
x[1,] <- c(1,0)
for(i in 1:99){
  x[i+1,] <- A%*%x[i,]
}
plot(x[,1], type="l", ylab = " ", xlab = "tempo")
lines(x[,2], type = "l", col = 2)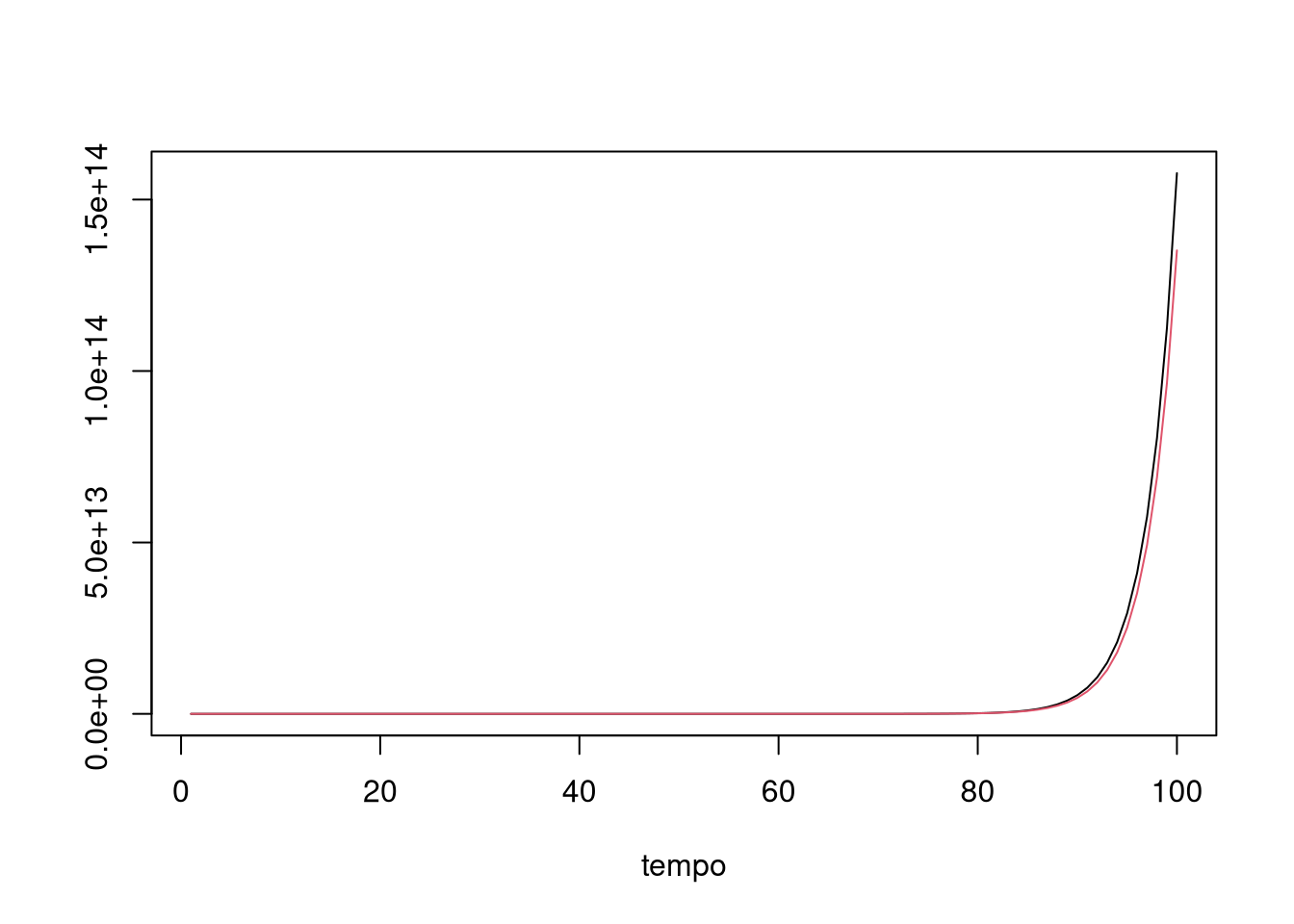

Um sistema não explosivo vai voltar a um estado de “repouso” do sistema. Veja que isso soa familiar: nós esperamos que a economia saia do equilíbrio mas volte a ele (ou a um novo equilíbrio). Como podemos saber se um sistema dinâmico linear é explosivo ou não?

A resposta são os autovalores da matriz \(A\) - na verdade, apenas o maior deles (em módulo). A ideia aqui é que a matriz \(A\) possa ser decomposta em seus autovalores e autovetores. Seja \(\Lambda\) uma matriz que tem na diagonal os autovalores e fora dela zero; e \(P\) uma matriz que tem os autovetores. Então, \(A = P\Lambda{}P^{-1}\). Mais ainda, \(A^j = P\Lambda^jP^{-1}\), onde \(\Lambda^j\) é equivalente a elevar cada entrada da diagonal a \(j\). Mostrar isso é fácil. Pense no caso \(A^2\). Se a decomposição por autovalor vale, \(A^2 = A \times A = P \Lambda P^{-1} P \Lambda P^{-1} = P \Lambda^2P^{-1}\), onde a última igualdade eu só usei o fato que \(P^{-1}P = I\), onde \(I\) é a matriz identidade. Logo, toda a dinâmica do sistema é governada pelos autovalores!

Para provar o ponto, eis os autovalores da matriz A do exemplo anterior:

eigen(A)

## eigen() decomposition
## $values
## [1] 1.4 0.1
## 
## $vectors
##           [,1]       [,2]
## [1,] 0.7592566 -0.7071068
## [2,] 0.6507914  0.7071068

O maior deles é 1,4. Qualquer autovalor maior que 1 gera um comportamento explosivo, já que elevar ele a números cada vez maiores gera números maiores. Um autovalor menor que 1 gera um sistema bem comportado, já que conforme elevamos ele a números maiores ele vai diminuindo. Para ilustrar o ponto, vou gerar um sistema estacionário:

B <- rbind(c(0.8,-0.4),c(0.6,-0.5))
eigen(B)

## eigen() decomposition
## $values
## [1]  0.5772002 -0.2772002
## 
## $vectors
##           [,1]      [,2]
## [1,] 0.8736212 0.3481078
## [2,] 0.4866066 0.9374545

x <- matrix(0,ncol = 2, nrow = 20)
x[1,] <- c(1,0)
for(i in 1:19){
  x[i+1,] <- B%*%x[i,]
}

plot(x[,1], type="l", ylab = " ", xlab = "tempo")
lines(x[,2], type = "l", col = 2)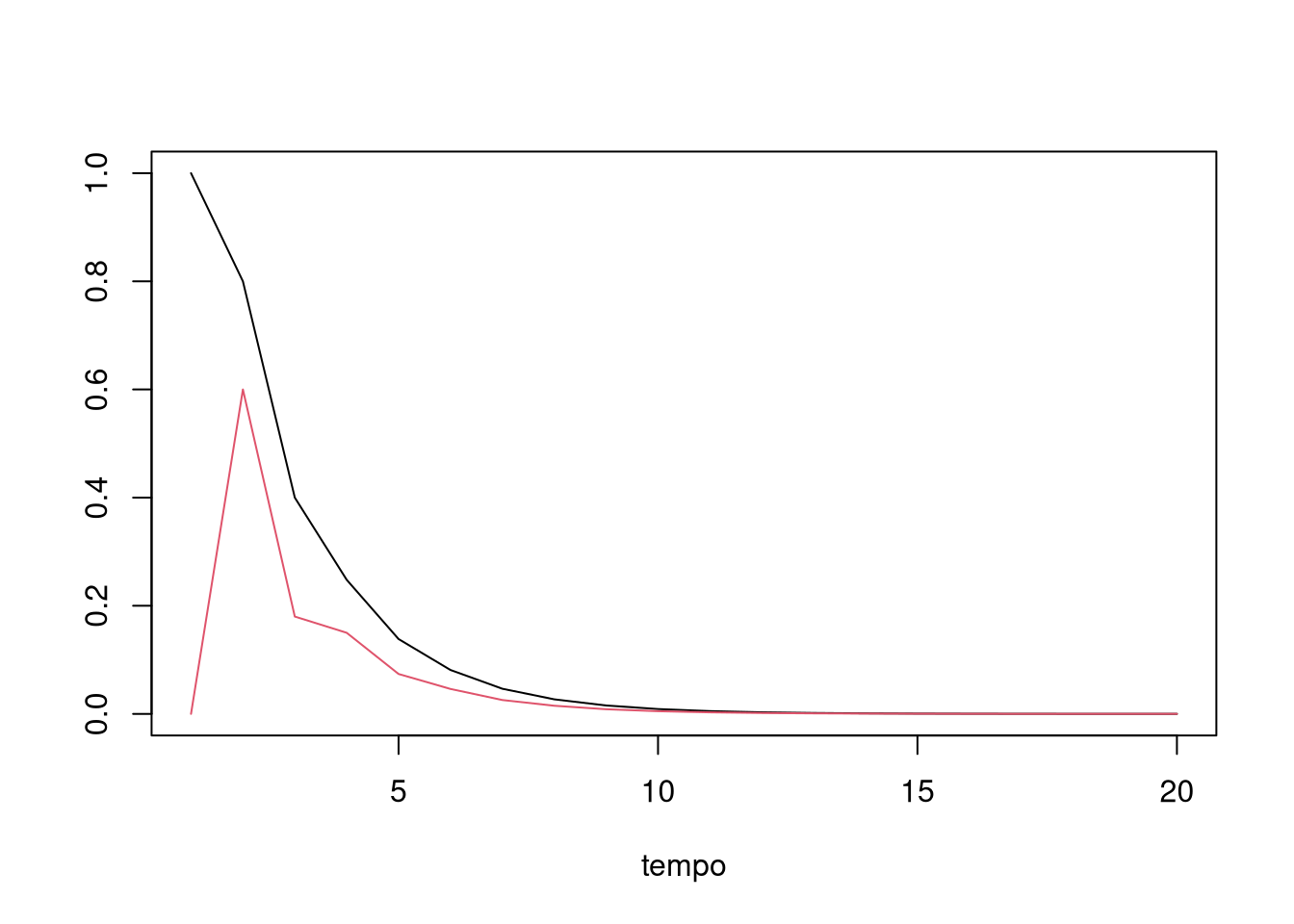

Veja que, nesse caso, o sistema converge para o vetor (0,0). Com o maior autovalor menor que 1, isso é sempre verdade. Apesar disso parecer excessivamente rigído, podemos sempre pensar que o vetor \(x\) representa desvios do equilíbrio e o equilíbrio é basicamente o que a gente quiser. Talvez um caso mais fascinante é quando nós temos o maior autovalor igual a 1. O autovetor associado vai ser o equilíbrio do sistema. Neste caso, o autovetor é um ponto fixo do sistema também - um tema que o Pedro falou um pouco sobre aqui. O exemplo abaixo ilustra isso, onde a linha verde representa o equilíbrio:

C = rbind(c(0.8,0.2),c(0.4,0.6))
eigen(C)

## eigen() decomposition
## $values
## [1] 1.0 0.4
## 
## $vectors
##           [,1]       [,2]
## [1,] 0.7071068 -0.4472136
## [2,] 0.7071068  0.8944272

ee <- eigen(C)$vectors[,1]/(eigen(C)$vectors[1,1]+eigen(C)$vectors[2,1])
y <- matrix(0,ncol = 2, nrow = 30)
y[1,] <- c(0.6,0.4)
for(i in 1:29){
  aux <- C%*%y[i,]
  y[i+1,] <- aux/sum(aux)
}
plot(y[,1], type="l", ylab = " ", xlab = "tempo", ylim = c(min(y),max(y)))
lines(y[,2], col = 2)
lines(1:30,rep(ee[1],30), col = 3)
legend("topright",legend = c("Componentes do ","sistema dinâmico", "Autovetor associado ao autovalor 1"), lty = c(1,1,1), col = c(1,2,3))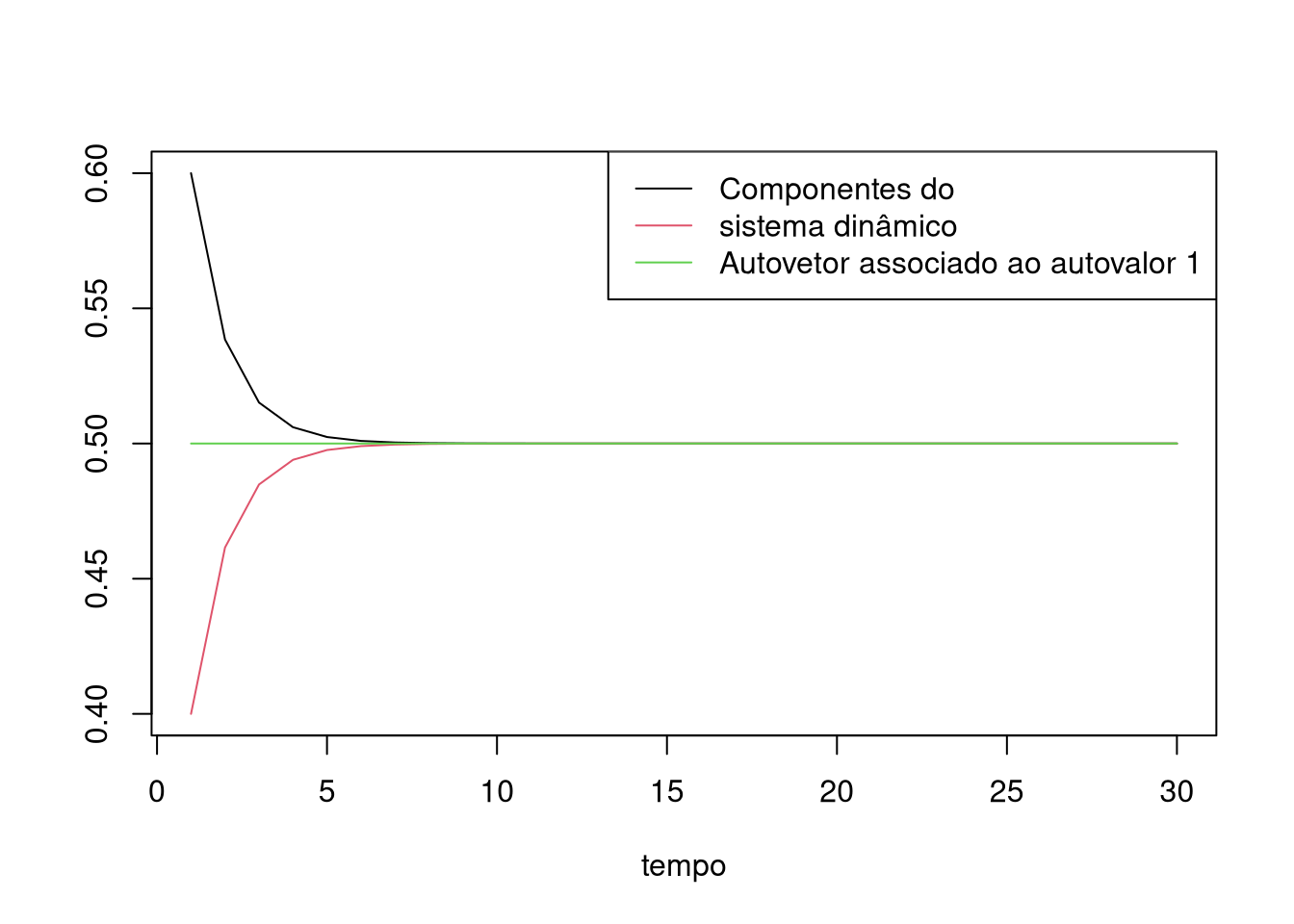

Como um autovetor vezes um escalar é também um autovetor, eu escolhi o autovetor que somando os componentes, é igual 1. Isso permite interpretar o autovetor como a probabilidade (incondicional), em equilíbrio, de cair em qualquer um dos dois estados.

Veja que a matriz \(C\), que governa a evolução do sistema, é tal que cada linha soma 1. Isso nos permite interpretar cada entrada \(c_{ij}\) como a probabilidade de migrar do estado \(j\) se estamos no estado \(i\). Cada mudança de estado no sistema depende exclusivamente de qual era o estado anterior do sistema (matematicamente, \(P(x_t |x_{t-1},x_{t-2},x_{t-3},...) = P(x_t|x_{t-1})\)): este tipo de processo recebe o nome de Cadeia de Markov. Um AR(1) é um exemplo de um processo de Markov também.

Autovalores são importantes para entender como sistemas dinâmicos se comportam, e dão uma excelente ilustração de uma aplicação de Algebra Linear em economia.