Programação Dinâmica IIB
No post passado eu falei sobre programação dinâmica para o caso com tempo finito. Se você não leu, leia: o resto do post não faz sentido sem ler a primeira parte. Vamos finalmente tratar de programação dinâmica em tempo infinito. Relembrando o nosso exemplo é o caso de um consumidor que tem que escolher quanto poupar. Formalmente, queremos resolver um problema do tipo:
\[Max \sum_{t=1}^{\infty} \beta^t u(c_t) \text{ sujeito a } k_{t+1} = (1-\delta)k_t + f(k_t) - c_t \]
A nossa estratégia no post passado era, para cada \(t\), resolver o problema:
\[V_t(k_t) = Max_{c_t}{} u(c_t) + \beta{} V_{t+1}((1-\delta{}) k_{t})+f(k_t)-c_t) \]
Onde nós sabiamos que o \(V_T(k_T)\) era igual a função utilidade avaliada em \(k_T\). Ou seja, o agente consumia todo o estoque de capital no último período. Usavamos esse fato para computar \(V_{T-1}\), e dai \(V_{T-2}\)…
Mas agora, somos apresentados a um problema em que não temos um último período, então não podemos prosseguir recursivamente. Apesar disso parecer um grande problema, é uma grande vantagem: o problema de hoje é idêntico ao problema de amanhã. Como em qualquer período nós ainda temos infinitos períodos a frente, nós podemos escrever o problema do consumidor usando um único \(V(k_t)\) - apesar do valor de \(k_t\) depender do período, a função \(V(k_t)\) não depende mais do período. Nosso novo problema é resolver:
\[ V(k_t) = \max_{c_t} u(c_t)+ \beta{} V((1-\delta)k_{t}+f(k_t)-c_t)) \]
A beleza de resolver esse problema é que, apesar de não sabermos o valor de \(V\), podemos iterar no computador e encontrar uma aproximação. Isso se deve ao fato de que o problema acima é uma contração, então vale o Teorema do Ponto Fixo de Banach, que o Pedro apresentou aqui. Nosso pseudo-código seria:
- Dê algum chute inicial para \(V\). Vamos chamar de \(V_0\).
- Resolva \(\max_c u(c) + \beta{}V_0((1-\delta)k_{t}+f(k_t)-c))\). Salve isso como \(V_1\)
- Resolva \(\max_c u(c) + \beta{}V_1((1-\delta)k_{t}+f(k_t)-c))\). Salve isso como \(V_2\)
- Faça isso até \(V\) ou \(c\) convergirem, i.e., até \(V_{i}\) e \(V_{i+1}\) (ou \(c_i\) e \(c_{i+1}\)) ficarem próximos numericamente
Vamos continuar com o nosso exemplo de função utilidade log e função de produção Cobb-Douglas. O caso em que \(\delta = 1\) tem solução fechada, então para a gente checar que tudo funcionou direitinho, eu vou implementar ele. Vamos dar, como chute inicial, a função valor sendo idêntica ao valor do capital. É um chute tosco, mas justamente por isso é ilustrativo. Eu sequer vou me preocupar em colocar uma checagem de convergência, para deixar o código o mais simples possível: deixe o computador repetir umas 150 vezes a operação.
using Optim
using Interpolations
using Plots
u(c)=log(c)## u (generic function with 1 method)
bet = 0.9## 0.9alf = 0.5## 0.5
f(x)=x^alf## f (generic function with 1 method)
y = range(0.1,stop = 10,length = 200)## 0.1:0.04974874371859297:10.0
guess = y## 0.1:0.04974874371859297:10.0vals = Array{Float64}(undef,150,length(y))## 150×200 Array{Float64,2}:
## 5.02741e-315 2.122e-314 … 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 5.02741e-315 5.02741e-315 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 5.02741e-315 2.122e-314 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 5.02741e-315 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 0.0 5.02741e-315 … 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 0.0 5.02741e-315 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 0.0 5.02741e-315 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 0.0 5.02741e-315 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 0.0 2.122e-314 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## ⋮ ⋱ ⋮
## 0.0 5.02762e-315 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 5.02741e-315 2.122e-314 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 0.0 5.02762e-315 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 5.02741e-315 2.122e-314 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 5.02741e-315 5.02761e-315 … 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 5.02741e-315 2.122e-314 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 5.02742e-315 5.02761e-315 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 2.122e-314 2.122e-314 0.0 0.0 0.0 0.0 0.0 0.0 0.0
## 5.02741e-315 5.02742e-315 0.0 0.0 0.0 0.0 0.0 0.0 0.0pol=Array{Float64}(undef,150,length(y))## 150×200 Array{Float64,2}:
## 0.0 5.0427e-315 4.14967e-315 … 3.913e-321 6.76376e-321
## 0.0 -1.05659e270 0.0 8.48798e-314 8.48798e-314
## 0.0 0.0 0.0 4.98512e-321 8.95741e-321
## 0.0 0.0 0.0 4.01181e-321 6.86257e-321
## 0.0 0.0 0.0 8.48798e-314 1.9098e-313
## 1.50237e-311 1.20954e-312 1.08222e-312 … 4.98512e-321 7.11455e-322
## 1.60423e-313 1.60468e-313 1.59848e-313 4.11063e-321 6.92186e-321
## -1.1409e-310 -1.41251e-310 -1.68413e-310 8.48798e-314 1.9098e-313
## 0.0 0.0 0.0 4.98512e-321 9.48606e-322
## 0.0 0.0 0.0 4.20944e-321 6.99103e-321
## ⋮ ⋱
## 5.0427e-315 5.04271e-315 5.04272e-315 6.49696e-321 8.38429e-321
## 5.0427e-315 5.04271e-315 5.04272e-315 1.9098e-313 1.2732e-313
## 5.04271e-315 5.04271e-315 5.04272e-315 4.74303e-322 4.15015e-321
## 5.04271e-315 5.04271e-315 5.04272e-315 6.55625e-321 8.41394e-321
## 4.19626e-315 4.19641e-315 4.19692e-315 … 8.48798e-314 1.2732e-313
## 4.19626e-315 4.19641e-315 4.19692e-315 8.83883e-321 4.19956e-322
## 4.14995e-315 4.14967e-315 4.19657e-315 6.66495e-321 8.4337e-321
## 4.15027e-315 4.14968e-315 4.19657e-315 8.48798e-314 1.2732e-313
## 5.0427e-315 4.1498e-315 4.19657e-315 8.95741e-321 4.44659e-322
vals[1,1:length(y)] = guess## 0.1:0.04974874371859297:10.0pol[1,1:length(y)] = y## 0.1:0.04974874371859297:10.0
for i=1:149
V=LinearInterpolation(y,vals[i,:],extrapolation_bc = Interpolations.Line())
for j = 1:length(y)
That(c)=-(u(c)+bet*V(f(y[j]-c)))
op = optimize(That,0,y[j])
vals[(i+1),j]=-Optim.minimum(op)
pol[(i+1),j]=Optim.minimizer(op)
end
end
A solução verdadeira é \(c^*(y) = (1-\alpha \beta)y\). Vamos plotar a solução verdadeira contra a estimada:
sol(Y)=(1-alf*bet)*Y## sol (generic function with 1 method)
plot(y,pol[150,1:length(y)] , lab = "Solução estimada", lw = 2, legend = :topleft)
plot!(y,sol(y), lab = "Solução verdadeira", linestyle = :dash, lw = 2)
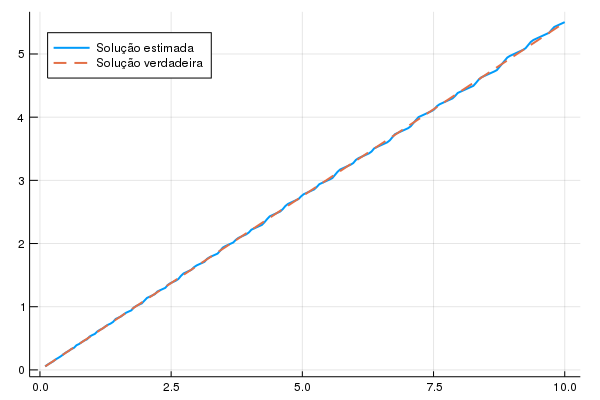
A linha da solução computada parece muito próxima da solução verdadeira, mas um pouco menos suave. A diferença parece ficar pior no final. Vamos fazer um gráfico com a diferença entre as duas soluções:
dif = sol.(y) - pol[150,:]## 200-element Array{Float64,1}:
## 0.05500000000000001
## 0.08236180904522614
## 0.10972361809045227
## 0.1370854271356784
## 0.16444723618090454
## 0.19180904522613068
## 0.2191708542713568
## 0.24653266331658294
## 0.2738944723618091
## 0.3012562814070352
## ⋮
## 5.281105527638191
## 5.308467336683417
## 5.335829145728644
## 5.36319095477387
## 5.3905527638190955
## 5.417914572864322
## 5.445276381909548
## 5.472638190954774
## 5.5
plot(y,dif, legend = :none, lw = 2)
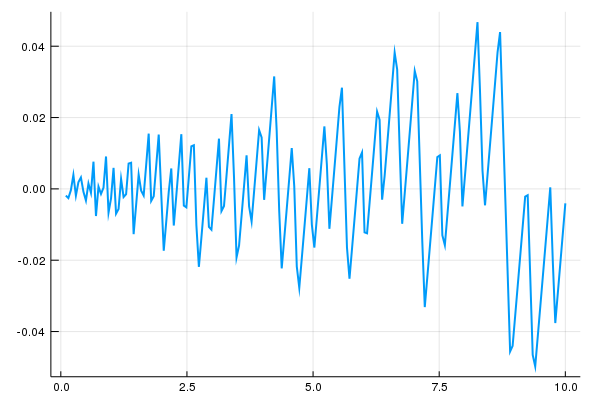
O gráfico deixa bem claro que a solução difere mais na ponta direita. Mas mesmo assim a diferença é pequena, apenas na segunda casa decimal.
Este post encerra a série de posts (introdutórios) sobre programação dinâmica. Esse tipo de ferramenta é importante em diversas aplicações em economia, tanto macro, desenvolvimento, e organização ondustrial. Muitas variações do problema não são resolvidas de maneira analítica: veja que mesmo no caso acima, em que a função de produção é Cobb Douglas e a utilidade é logarítmica, precisamos que o capital se deprecie totalmente; caso contrário, não temos solução analítica. Esse caso é interessante e pode ser obtido alterando o código acima minimamente.
Este post é, basicamente, uma adaptção deste post, do quant-econ, do Sargent e Stachurski