Visualizando comportamento de uma distribuição e de processos autoregressivos com o gganimate

Dia desses o gganimate finalmente foi liberado no CRAN e agora é instalável na sua máquina simplesmente executando o comando install.packages("gganimate") - mas se prepare porque ele têm muitas dependências. Muita gente esperava esse pacote porque até então, animações com a qualidade e gramática do ggplot2 não eram humanamente possíveis. Você teria que renderizar e salvar todos os frames da animação e depois junta-las com software externo. Foram quase três anos de desenvolvimento, entre o primeiro commit no GitHub e o lançamento oficial no CRAN e muita coisa mudou no meio do caminho, especialmente porque o pacote que começou sendo desenvolvimento por Dave Robinson eventualmente trocou para as habilidosas mãos do dinamarquês Thomas Lin Pedersen, que desenvolve vários pacotes excelentes de R. Entre eles, três extensões ao ggplot2, ggraph para plotar grafos, ggforce com uma gramática expandida e o gganimate.

Pra quem não sabe, o “gg” de ggplot2 significa grammar of graphs. Faz parte da filosofia interessante dos pacotes do tidyverse oferecer uma gramática de um assunto. O ggplot2 não só produz visualizações de alta qualidade, ele oferece uma linguagem comum para isso. A ideia é criar camadas e adicionar uma sobre a outra. É bem modular, por isso existem dezenas de expansões ao ggplot2 que conversam perfeitamente com o pacote base e usam a mesma gramática, só adicionando verbos novos. Aqui tem uma lista interessante.

Um desafio no desenvolvimento do gganimate era pensar em uma gramática das animações. Quem usou o pacote na versão ainda em desenvolvimento do Robinson logo percebeu que ele entendia a animação como um eixo na qual o usuário iria variar a visualização. Era só adicionar uma linha dizendo qual variável indexaria os frames da animação e pronto, parecia mais um parâmetro do gráfico. Isso mudou.

Nesse post aqui Pedersen explica brevemente como funciona a nova gramática e o spoiler que eu posso dar é que ela diferencia duas coisas fundamentais que antes eram a mesma: scenes e segues. Uma scene é só uma sequência de dados diferentes sendo exibidos no que fundamentalmente é a mesma estética base. Uma segue representa mudanças na estética base do da visualização.

Vamos fazer uma pequena simulação aqui para exemplificar comportamento assintótico de uma distribuição de probabilidade. Se você jogar um dado, guardar o número, jogar de novo, guardar o número e por aí vai… A média desses números vai para algum lugar?

Vai, e sabemos para onde. Chamemos de \(D\) a distribuição discreta que representa um dado não-viciado, temos \(\mathbb{E}[D] = \sum_{i = 1}^6 \frac{i}{6} = 3.5\)

library(TeachingDemos)
library(tidyverse)
library(gganimate)

set.seed(10)
n = 1500
numeros = dice(rolls = n, 
               ndice = 1)
numeros = numeros[[1]] # precisamos fazer isso porque a função dice() é louca
media = vector()

for(i in 1:n) {
  
  media[i] = mean(numeros[c(1:i)])
  #armazenamos a média das jogadas na i-ésima jogada
}

base = tibble(media = media,
              indice = seq(from = 1,
                           to = n,
                           by = 1))

base %>%
  ggplot(aes(x = indice, y = media)) +
  geom_line(size = 1.5) + 
  geom_hline(yintercept = 3.5) + # linha vertical na experança
  labs(caption = "Elaboração: Pedro Cavalcante, disponível em azul.netlify.com")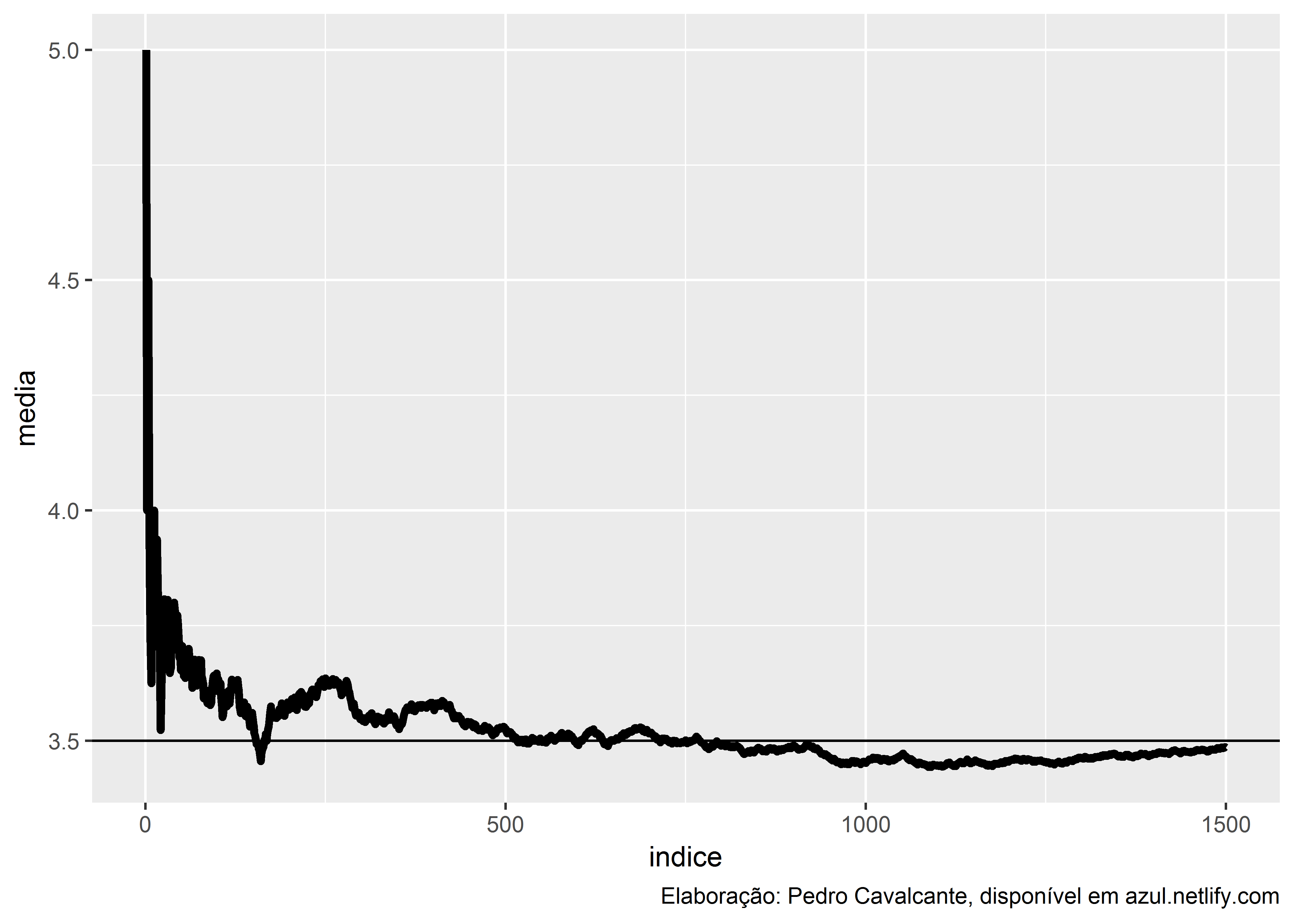

last_plot() +
  transition_reveal(indice)

anim_save("animacao1.gif")

Outra coisa interessante de ver é a diferença entre processos autoregressivos com e sem raízes unitárias, o que os diferencia entre estacionário e não-estacionário.

library(tidyverse)
set.seed(1234)

n = 500
inicial = rnorm(1)
inercia = .8

estacionario = vector()
estacionario[1] = inicial

n_estacionario = vector()
n_estacionario[1] = inicial

for(i in 2:n) {
  
  choque = rnorm(1, sd = .5)
  
estacionario[i] = estacionario[i-1] * inercia + choque  
n_estacionario[i] = n_estacionario[i-1] + choque

  }


AR = tibble::tibble(estacionario = estacionario,
            n_estacionario = n_estacionario,
            indice = seq(from = 1,
                           to = n,
                           by = 1))


AR %>%
  ggplot(aes(x = indice)) + 
  geom_line(aes(y = estacionario),
            size = 1.2,
            color = "#5b97f7") + 
  geom_line(aes(y = n_estacionario), 
            size = 1.2,
            color = "#ed6840") +
  labs(caption = "Elaboração: Pedro Cavalcante, disponível em azul.netlify.com")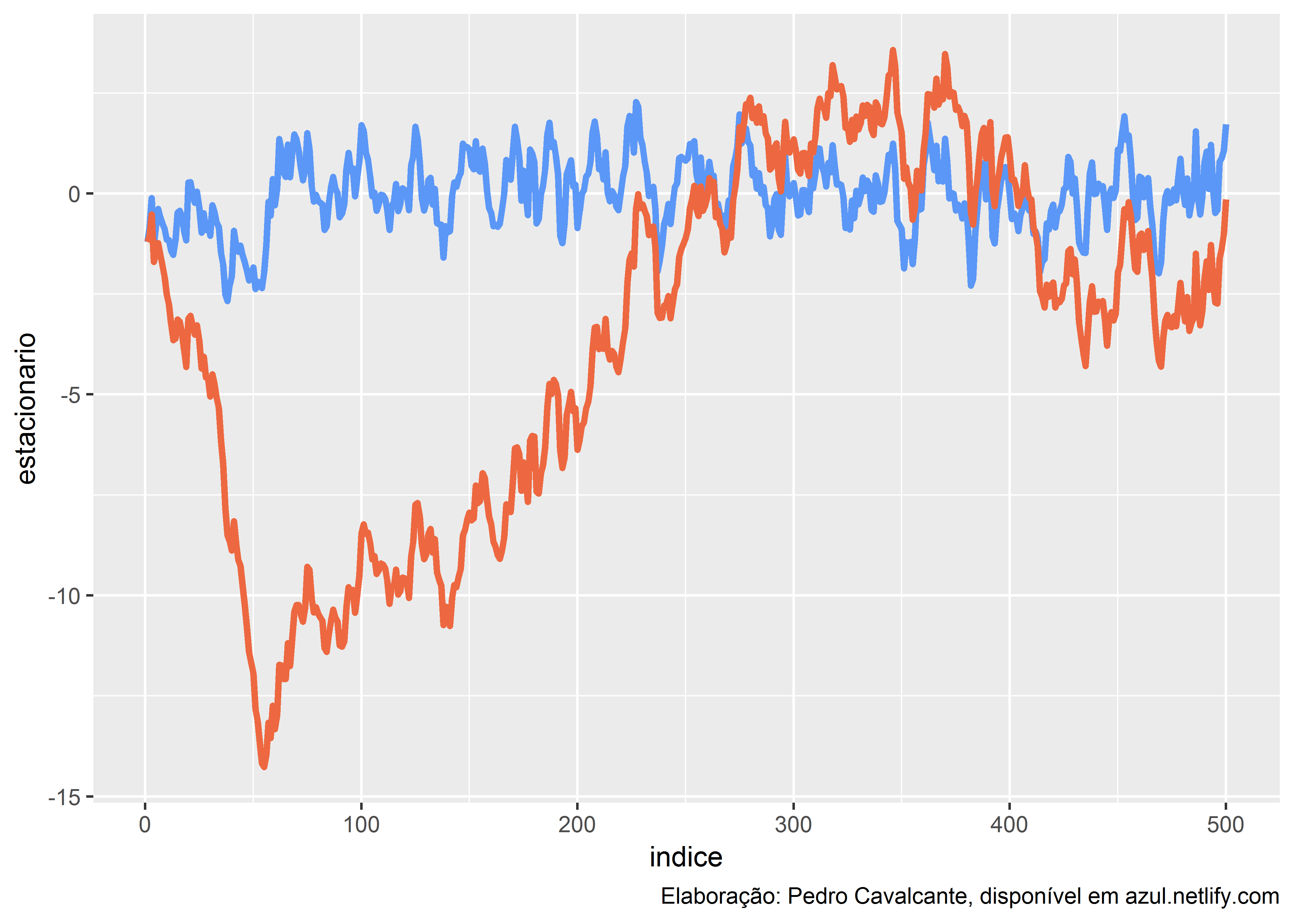

last_plot() + 
  transition_reveal(indice)

anim_save("animacao2.gif")