Aplicando Programação Dinâmica à Reforma da Previdência
Nota: Originalmente o problema do agente, que é a primeira equação deste post, estava \(\beta\) e não \(\beta^t\). Se tratava de um typo. Agradeço a Marcelo Moraes pela observação
Nós no Azul não discutimos políticas públicas diretamente. Muitos outros sites, com autores competentes, o fazem. É uma simples questão de vantagens comparativas. Mas nós nos contagiamos pelo clima da reforma da previdência, como quase todos os economistas. E a reforma da previdência vem a ser um excelente tema para ser explorado usando programação dinâmica, que eu já tratei aqui no blog em outras ocasiões.
Vamos pensar em um agente que recebe um salário \(\omega\) e pode escolher poupar ou consumir. Ele sabe que em uma certa idade ele vai se aposentar e passar a receber uma aposentadoria \(s\). Qual a escolha ótima desse agente? Nós nos fizemos uma pergunta similar em posts anteriores e lá - como aqui - eu vou adotar algumas hipóteses simplificadoras (como de praxe):
- O salário é um processo i.i.d. Eu vou usar a distribuição Gama(5,1), que tem suporte finito e nos números positivos - como se espera de um salário.
- O agente sabe exatamente quanto tempo ele vai viver e exatamente quanto tempo ele vai trabalhar. O primeiro é polêmico, mas ele facilita enormemente as contas e é mais realista do que supor que o agente se planeja para o infinito quando ele pensa na aposentadoria. O segundo é relativamente realístico.
- Existe um único ativo que paga uma taxa de juros \(r\).
- O agente não pode se endividar. Isso facilita a vida na hora de resolver o problema de otimização (numericamente) e é uma maneira muito fácil de evitar esquemas em que o agente se endivida ao infinito. Relaxarei essa hipótese em outro post.
Então o problema do agente é:
\[Max_{\{c_t\}_{t=0}^T} \displaystyle \sum_{t=0}^T \beta^t E(u(c_t)) \text{ sujeito a } a_{t+1} = (1+r)a_t + W_t - c_t \]
Onde
\[W_t = \begin{cases} \omega_t & \text{se } 0 \leq t \leq T_{aposentadoria}\\ s & \text{se } T_{aposentadoria} \leq t \leq T\\ \end{cases}\]
Veja que isso gera uma quebra no nosso problema de programação dinâmica: de um ponto em diante a dotação muda completamente, inclusive deixando de ser aleatória. Vamos resolver isso de uma maneira muito esperta, como sugerida no site do quant.econ:
- Resolva recursivamente o problema do agente aposentado, sabendo que no fim da vida dele o ótimo é gastar todos os ativos. (Como já fizemos)
- Use a função Valor do primeiro período do agente aposentado como o valor terminal do problema do agente que trabalha
- Resolva recursivamente o problema do agente que trabalha
Ou seja, quebramos o problema do agente em dois problemas separados e ressolvemos eles separadamente, com a ligação entre eles feita pela função valor dos dois problemas.
O programa em Julia que resolve o problema segue abaixo. Eu uso w para gerar o grid de riqueza e utilizo a utilidade log. Eu inicialmente coloco um agente trabalhando 65 anos e vivendo 20 anos aposentado, um total de 85 anos. O valor da aposentadoria é 1. A média da distribuição Gama(5,1) é 5, então nossa aposentadoria é bem menor que o que o agente vai ganhar em média durante a vida.
#Carregando os pacotes que precisamos
using Distributions
using Plots
using Interpolations
using Statistics
using Optim
d = Gamma(5,1)
w = range(0.01,stop=300,length=1000)
u(c) = log(c)
bet = 1/(1+r)
work_age = 65
s = 1
ret_age = 20
#Resolvendo o problema do aposentado
choice_ret = zeros(ret_age,length(w))
value_ret = zeros(ret_age,length(w))
value_ret[1,:] = u.(w)
choice_ret[1,:] = w
for j in 2:ret_age
f = LinearInterpolation(w,value_ret[j-1,:], extrapolation_bc = Line())
for i in 1:length(w)
val(c) = -(u(c) + bet*f((1+r)*w[i] -c + s))
otm = optimize(val,0,w[i])
choice_ret[j,i] = Optim.minimizer(otm)
value_ret[j,i] = -Optim.minimum(otm)
end
println("Iteration ", j)
end
#Resolvendo o problema do trabalhador
value_trab = zeros(work_age,length(w))
choice_trab = zeros(work_age,length(w))
value_trab[1,:] = value_ret[ret_age,:] #Colocando a função Valor do aposentado como condição final do problema do trabalhador
choice_trab[1,:] = choice_ret[ret_age,:]
for k in 2:work_age
f = LinearInterpolation(w,value_trab[k-1,:], extrapolation_bc = Line())
for i in 1:length(w)
mm = rand(d,2000)
val(c) = -(u(c) + bet*mean(f.((1+r)*w[i] -c .+ mm)))
otm = optimize(val,0,w[i])
choice_trab[k,i] = Optim.minimizer(otm)
value_trab[k,i] = -Optim.minimum(otm)
end
println("Iteration ",k)
end
Podemos usar essas soluções e simular uma trajetória de salário para obter a escolha ótima de consumo e de poupança do agente. O código a seguir faz isso. Observe que, como em posts anteriores, eu deixei o primeiro elemento da matriz ser o último período do agente, então aqui eu preciso plotar e simular tudo de trás pra frente:
start = 2
wage = rand(d,65)
cons = zeros(85)
asset = zeros(85)
asset[85] = start
for k in 65:-1:1
cons_foo = LinearInterpolation(w,choice_trab[k,:], extrapolation_bc = Line())
cons[k+20] = cons_foo(asset[k+20])
asset[k+19] = (1+r)*asset[k+20] - cons[k+20] + wage[k]
end
for k in 20:-1:2
cons_foo = LinearInterpolation(w,choice_ret[k,:], extrapolation_bc = Line()) #also depends on the convergence of the previous program
cons[k] = cons_foo(asset[k])
asset[k-1] = (1+r)*asset[k] - cons[k] + s
end
cons[1] = asset[1]
rett = zeros(20)
fill!(rett,s)
income = [wage[65:-1:1]; rett]
plot(asset[85:-1:1], lab = "Assets", xlab = "Tempo",legend = :topleft)
plot!(cons[85:-1:1], lab = "Consumption")
plot!(income[1:85], lab = "Income")
vline!([66],lab = "Aposentadoria", lw = 2)Obtemos a seguinte imagem:
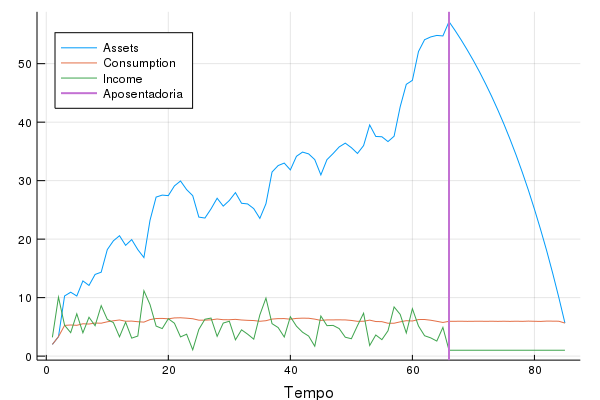
Várias coisas são interessantes nessa imagem e mostram como programação dinâmica formaliza a nossa intuição econômica:
O agente escolhe um nível de consumo que varia muito pouco ao longo da vida dele, apesar das largas variações na renda. Milton Friedman e Franco Modigliani são os “pais” dessa ideia, a hipótese de renda permanente
Como consequência direta de (1), o valor dos ativos do agente varia muito mais do que o consumo
Também como consequência de (1), o agente poupa durante a vida de trabalho dele e despoupa na aposentadoria. Veja a inflexão dos ativos exatamente onde passa a linha de aposentadoria.
Agora, podemos usar esse mesmo programa para nos perguntar como mudanças no esquema previdenciário afetam a decisão do agente. Por exemplo, o que acontece se eu mudar o valor que ele recebe aposentado para a média do que ele recebe na vida (5)? E para um valor maior, como 7? Nós vamos deixar o salário fixo em cada uma dessas simulações, ou seja, usaremos exatamente os mesmos valores sorteados de salários que foram usados para gerar a imagem acima. Assim, nós isolaremos o efeito de termos mudado apenas o valor pago na aposentadoria. Primeiro, como o consumo evolui para cada um dos casos:
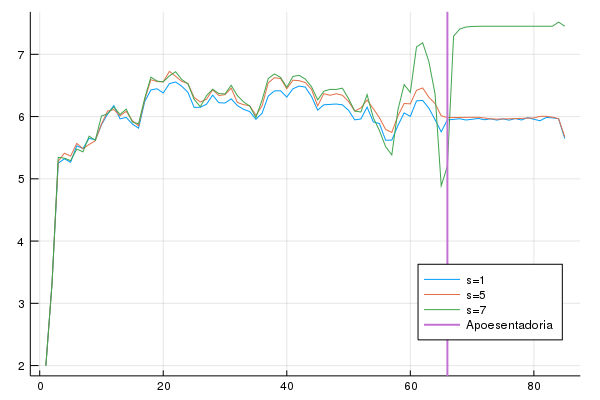
Veja que até os 20 anos o consumo não é muito diferente entre os 3 processos. No processo em que \(s=7\), o que acontece é que o consumo aumenta depois da aposentadoria. Isso é uma consequência de nós impedirmos endividamento e termos colocado uma aposentadoria muito acima da média do salário ganho pelo agente. Veja que, em geral, o consumo durante a vida toda é maior quanto maior for a aposentadoria. Vamos ver os ativos:
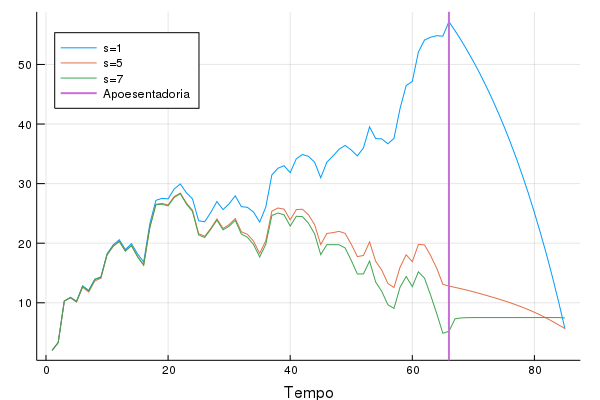
Aqui a diferença entre os diferentes valores poupados aparece claramente. Veja que um agente que espera uma aposentadoria baixa poupa muito mais que um agente que espera uma aposentadoria na média que ele recebia durante o empregado. Veja que isso tem implicações diretas em desenvolvimento, por exemplo, onde uma poupança maior está associado a mais capital e mais produto no estado estacionário (como no modelo de Solow) ou pode servir para financiar investimento em capital humano.
Outra maneira de vizualizar a mesma ideia é ver o consumo ótimo para cada nível de riqueza para cada um dos problemas. Eu escolhi um ponto arbitrário (a décima entrada em cada um deles, ou seja, faltando 10 anos para se aposentar) do tempo para comparar:
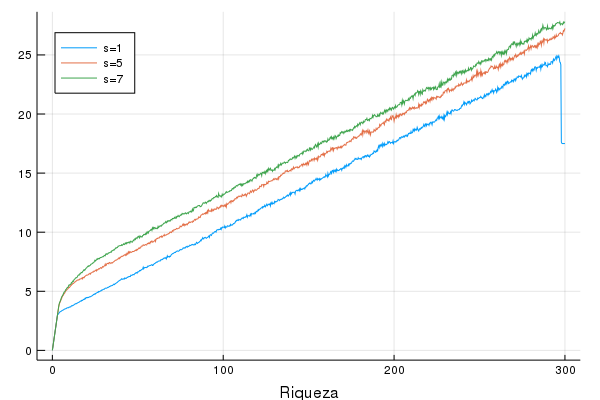
Veja que para valores maiores de \(s\), maior o nível de consumo dado a mesma riqueza. Veja que aqui o consumo ótimo depende da data que estamos olhando, ao contrário do problema em tempo infinito. Mas de forma geral as funções não mudam muito, e a imagem acima é bem representativa de se fossemos olhar período por período.
Salários crescendo no tempo
A hipótese de um salário i.i.d. é bastante irrealista. Espera-se que o salário do agente cresca com o tempo, conforme ele vai acumulando capital humano, por exemplo. Existem várias maneiras de inserir isso no modelo.
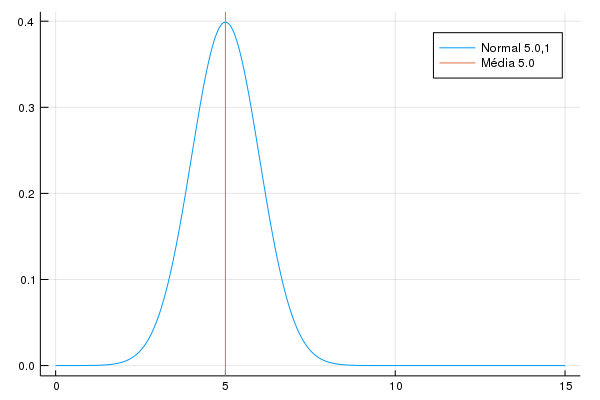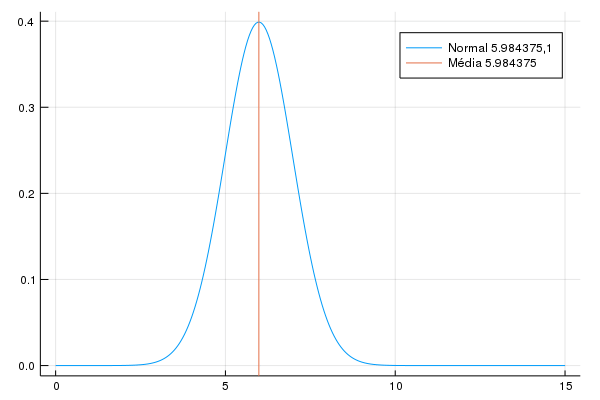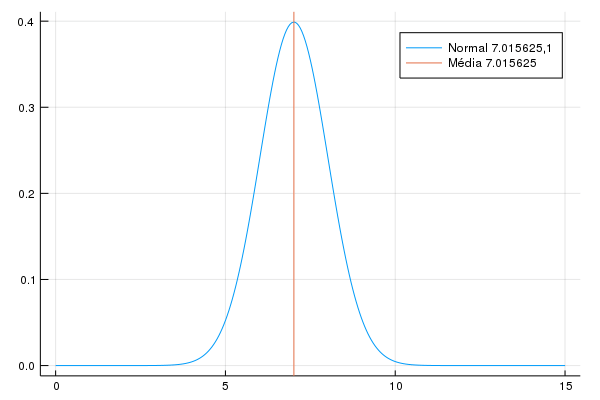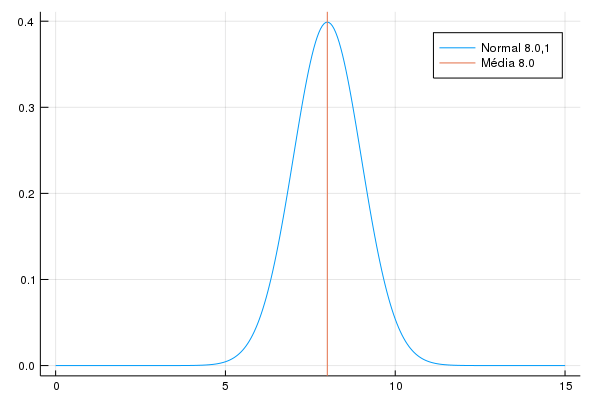
Eu vou adotar uma maneira curiosa, que vai envolver uma mudança de distribuição: a cada período o salário é distribuído usando uma \(Normal(\mu+\epsilon_t,\sigma)\), onde \(\epsilon_t\) é um aumento determinístico da média. Eu uso a normal ao invés da Gama porque a variância da distribuição Gama depende dos dois paramêtros: aumentar a média assim aumentaria a variância. Eu vou definir \(\epsilon_t\) de maneira que no último período a média seja 8, e vou colocar \(\mu = 5, \sigma = 1\). Isso coloca a probabilidade de um salário negativo virtualmente zero, já que exigiria mais de 5 desvios padrões para alcançarmos o zero. Veja que isso é equivalente a:
\[\omega_t = \epsilon_t + \mu + \sigma z,\quad z \sim N(0,1)\]
Eu escolho mudar direto na distribuição porque (a) eu testei inicialmente com a distribuição Gama onde a conta acima não é verdade (b) isso permite facilmente adicionar heterocedasticidade aos salários, o que eu não vou fazer. A animação abaixo (feita no Julia) mostra a ideia de como o salário vai mudar ao longo do tempo.
O código para estimar a melhor resposta nesse modelo muda apenas um pouco:
inc = range(0,stop=3,length=65) #esse é o epsilon_t da fórmula acima
inc = inc[65:-1:1] #Lembrem que eu faço tudo de trás pra frente
s = 1
choice_ret5 = zeros(ret_age,length(w))
value_ret5 = zeros(ret_age,length(w))
value_ret5[1,:] = u.(w)
choice_ret5[1,:] = w
#Nada muda aqui
for j in 2:ret_age
f = LinearInterpolation(w,value_ret5[j-1,:], extrapolation_bc = Line())
for i in 1:length(w)
val(c) = -(u(c) + bet*f((1+r)*w[i] -c + s))
otm = optimize(val,0,w[i])
choice_ret5[j,i] = Optim.minimizer(otm)
value_ret5[j,i] = -Optim.minimum(otm)
end
println("Iteration ", j)
end
value_trab5 = zeros(work_age,length(w))
choice_trab5 = zeros(work_age,length(w))
value_trab5[1,:] = value_ret5[ret_age,:]
choice_trab5[1,:] = choice_ret5[ret_age,:]
#Aqui a coisa muda: observe dd e y
for k in 2:work_age
f = LinearInterpolation(w,value_trab5[k-1,:], extrapolation_bc = Line())
y = 5+inc[k]
dd=Normal(y,1)
for i in 1:length(w)
mm = rand(dd,2000)
val(c) = -(u(c) + bet*mean(f.((1+r)*w[i] -c .+ mm)))
otm = optimize(val,0,w[i])
choice_trab5[k,i] = Optim.minimizer(otm)
value_trab5[k,i] = -Optim.minimum(otm)
end
println("Iteration ",k)
end
O código para gerar uma trajetória é idêntico, exceto na hora de gear o salário, que envolve uma ligeira mudança para alocar a mudança na distribuição:
wage5 = zeros(65)
for i in 65:-1:1
y = 5+inc[i]
dd=Normal(y,1)
wage5[i] = rand(dd,1)[1]
end
E o resto do código envolve apenas mudar quais arrays serão preenchidas e desenhadas. Vamos ver a trajetória de consumo, ativo, e renda:
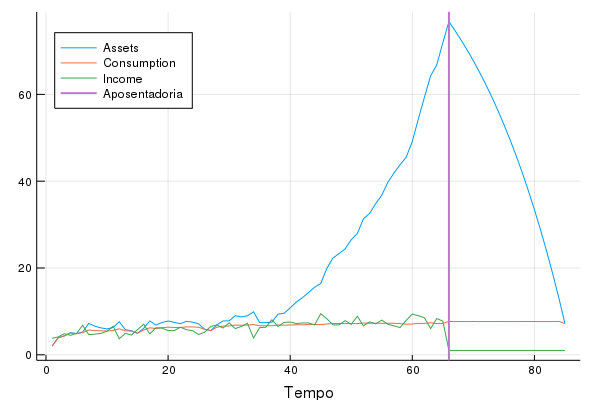
Veja que as principais características do problema se mantém. A trajetória dos ativos esconde quase toda a variação no consumo, então vamos fazer um gráfico sem os ativos:
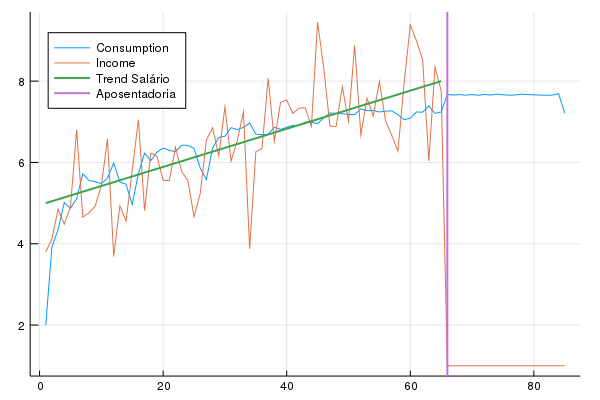
Veja que o consumo cresce ao longo do tempo junto com os salários, outra vez resultado da limitação do endividamento. Veja que mesmo com um seguro desemprego baixissimo, o agente poupa o suficiente para manter o consumo inalterado comparado com o final da vida.
Podemos fazer exercícios de estatíca comparativa e ver como o consumo e trajetória de acumulação de ativos se colocarmos uma aposentadoria maior (\(s=5\)). Vamos começar fazendo o gráfico do consumo:
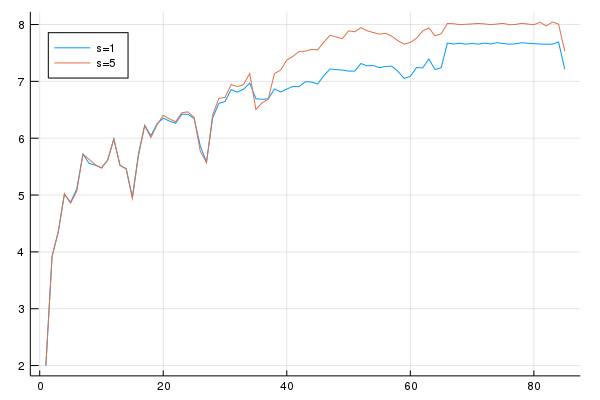
A diferença não é muito grande até por volta dos 40 anos, onde o consumo de quem tem uma aposentadoria maior fica maior do que o agente com aposentadoria \(s=1\). Vamos ver a trajetória dos ativos:
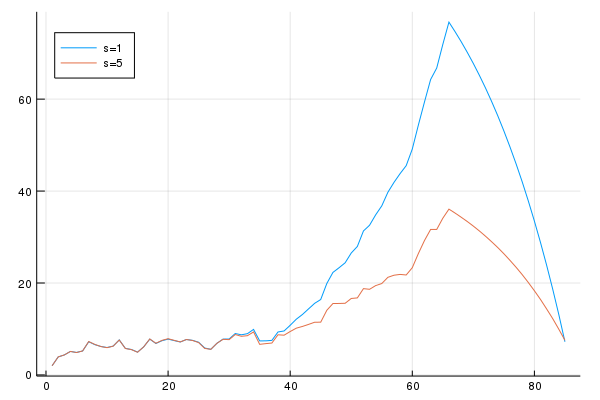
Assim como no caso i.i.d., a trajetória dos ativos dos os dois processos é a que mais chama atenção: o agente recebendo uma aposentadoria muito baixa poupa muito mais do que o agente que recebe aposentadoria alta.
Previdência é um tema que se encaixa perfeitamente no arcabouço de programação dinâmica. A resposta matemática/computacional é coerente com a intuição econômica: benefícios de aposentadoria mais generosos geram menores incentivos a poupar. Os agentes vão procurar suavizar o consumo.
Duas coisas ficaram faltando neste post: a primeira é permitir que o agente se endivide. Isso provavelmente terá repercuções no início da vida do agente, especialmente no caso em que o salário cresce ao longo do tempo: o agente vai querer suavizar o consumo tendo dívida hoje que serão pagas no futuro. Também faltou fazermos uma estática comparativa com a idade de aposentadoria: e se o agente vivesse 85 anos, mas só precisasse de 45 anos trabalhando para se aposentar? Quão brutal seriam as mudanças?
Prometo responder essas perguntas em breve.