Verificando algumas propriedades de Mínimos Quadrados com o R
Para você, bravo leitor que conseguiu superar o título horrível deste post e abriu o link, devo algo interessante. Já adianto que normalidade (assintótica) de um estimador não é lá o assunto mais empolgante do mundo. Fiz esse post pensando que esse tema faz parte da longa lista de assuntos tratados de maneira assustadoramente teórica em salas de aula pelo mundo. Consistência assintótica, convergência em distribuição e Teorema do Limite Central são excelentes conceitos para serem introduzidos com uma abordagem computacional, do ver acontecendo. É isso que eu quero mostrar hoje. Como de costume, esse blog é um espaço para falar de ideias da maneira como nós gostaríamos de ter sido introduzidos à elas.
Estimadores são regras para recuperar parâmetros de um conjunto de dados, assim sendo, são também variáveis aleatórias. Uma propriedade que variáveis aleatórias podem ter é normalidade, aderir à uma distribuição normal.
Derivar esse estimador tão conhecido do começo ao fim me parece um exercício de futilidade, existem dezenas/centenas de tratamentos absolutamente rigorosos e de altíssima qualidade disso. Eu particularmente gosto muito do manual de econometria do Hayashi e a abordagem de lá, se você quiser uma recomendação explícita de fonte.
Vamos focar na nossa vantagem comparativa aqui: recursos computacionais. Em particular, estamos interessados em propriedades em amostras grandes do estimador OLS. Como as estimativas pontuais dele se distribuem em relação ao verdadeiro parâmetro? Os parâmetros dessa distribuição são uma função das pertubações nos dados? Se sim, como respondem à variância dessas pertubações? Seguindo a convenção de notação a que fui apresentado, notarei \(\beta\) como o parâmetro verdadeiro e \(\hat{\beta}\) como o estimador.
Um resultado clássico e que seu professor certamente já regurgitou no quadro é que, dadas as condições de Gauss-Markov, o estimador OLS tem ditribuição normal com média no parâmetro verdadeiro e que - quase como consequência - a diferença das estimativas ao parâmetro verdadeiro converge em distribuição para uma normal com média \(0\).
\[\hat{\beta} \sim N(\beta, \sigma^2(X^T X)^{-1}) \]
Em que a variância do estimador é dada pelo produto da inversa da matriz de Gram dos dados e o termo de variância dos erros. Temos nada de sobrenatural aqui, só estamos dizendo que espera-se que o estimador “chute” bem e que se os erros tiverem mais variância a precisão dele diminui.
Verificando isso computacionalmente
De fato, podemos visualizar uma parte isso ocorrendo. Vamos definir \(X \sim U(10,20)\), \(u \sim N(0,\sigma)\). Com isso definiremos uma nova variável \(Y = 5 + 0,8 X + u\). Regrediremos uma variável na outra em variados tamanhos de amostra - de \(n=1\) até \(n=10000\) - e veremos como se comporta nosso estimador.
library(ggplot2)
library(dplyr)
set.seed(1234)
parametros = vector() # vetor vazio que será preenchido
variancia_estimador = vector()
m = 10000 # tamanho máximos de amostra
for(i in 1:m) {
X = runif(n = m, min = 10, max = 20) # n = 2000 de uma variável aleatória X ~ U(10,20)
u = rnorm(n = m) # pertubações aleatórias com distribuição u ~ N(0,1)
Y = 5 + 0.8*X + u # criamos Y a partir de X e u
dados = data.frame(explicada = Y,
explicativa = X)
modelo = lm(Y ~ X, # fórmula do modelo a ser estimado
data = dados) # data.frame em que estão as variáveis
parametros[i] = coef(modelo)[2] # pegamos somente o parâmetro estimado para X
variancia_estimador[i] = var(parametros)
}
df_parametros = data.frame(Estimado = parametros,
Amostra = 1:m) #criamos um dataframe para o ggplot2
df_parametros %>%
ggplot(aes(x = Estimado)) +
geom_histogram(aes(y = ..density..)) +
geom_vline(xintercept = .8, # linha vertical no parâmetro verdadeiro
size = 2) +
ylab("") +
xlab("Parâmetro estimado") +
labs(title = "Normalidade do estimador mínimos quadrados")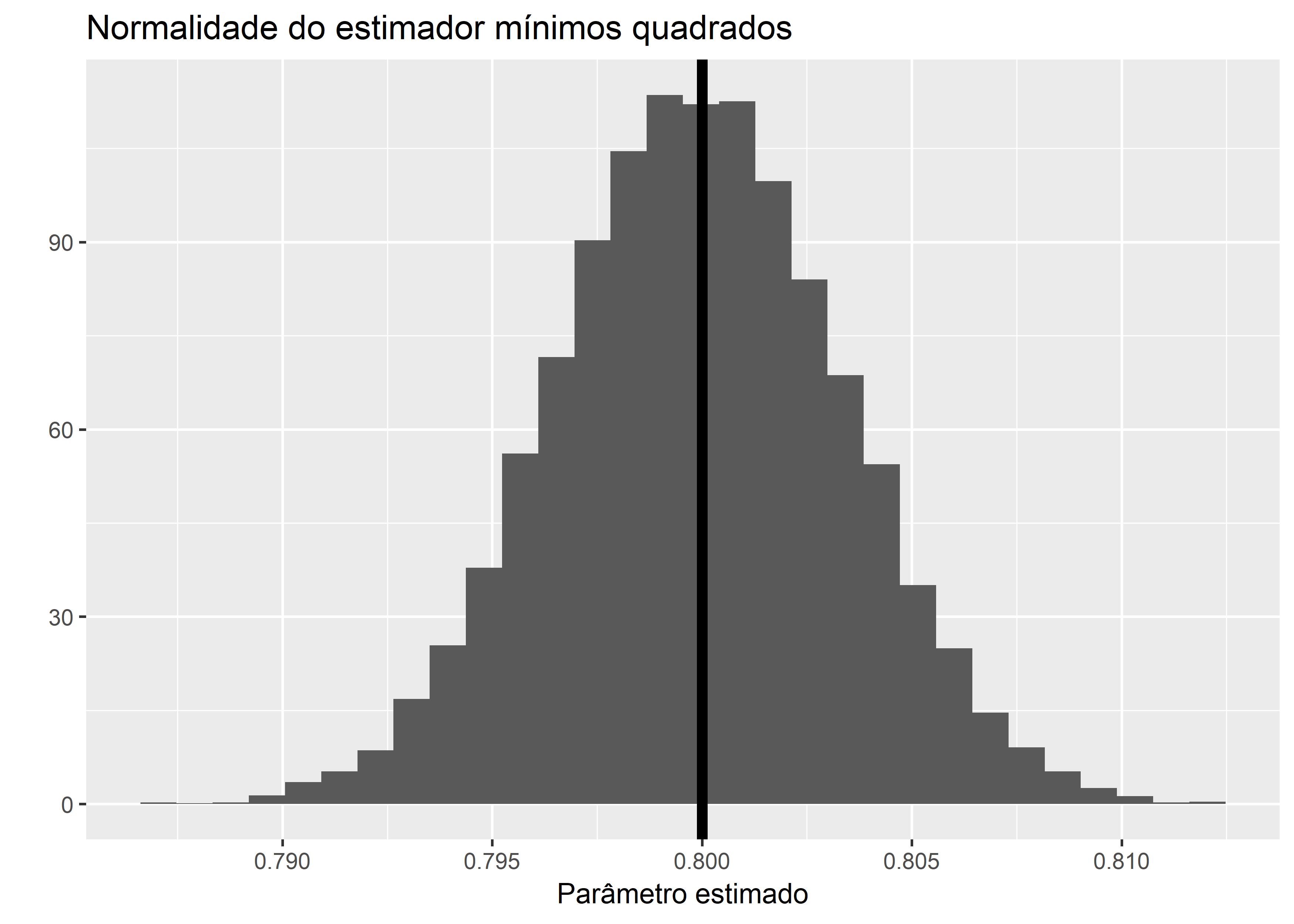
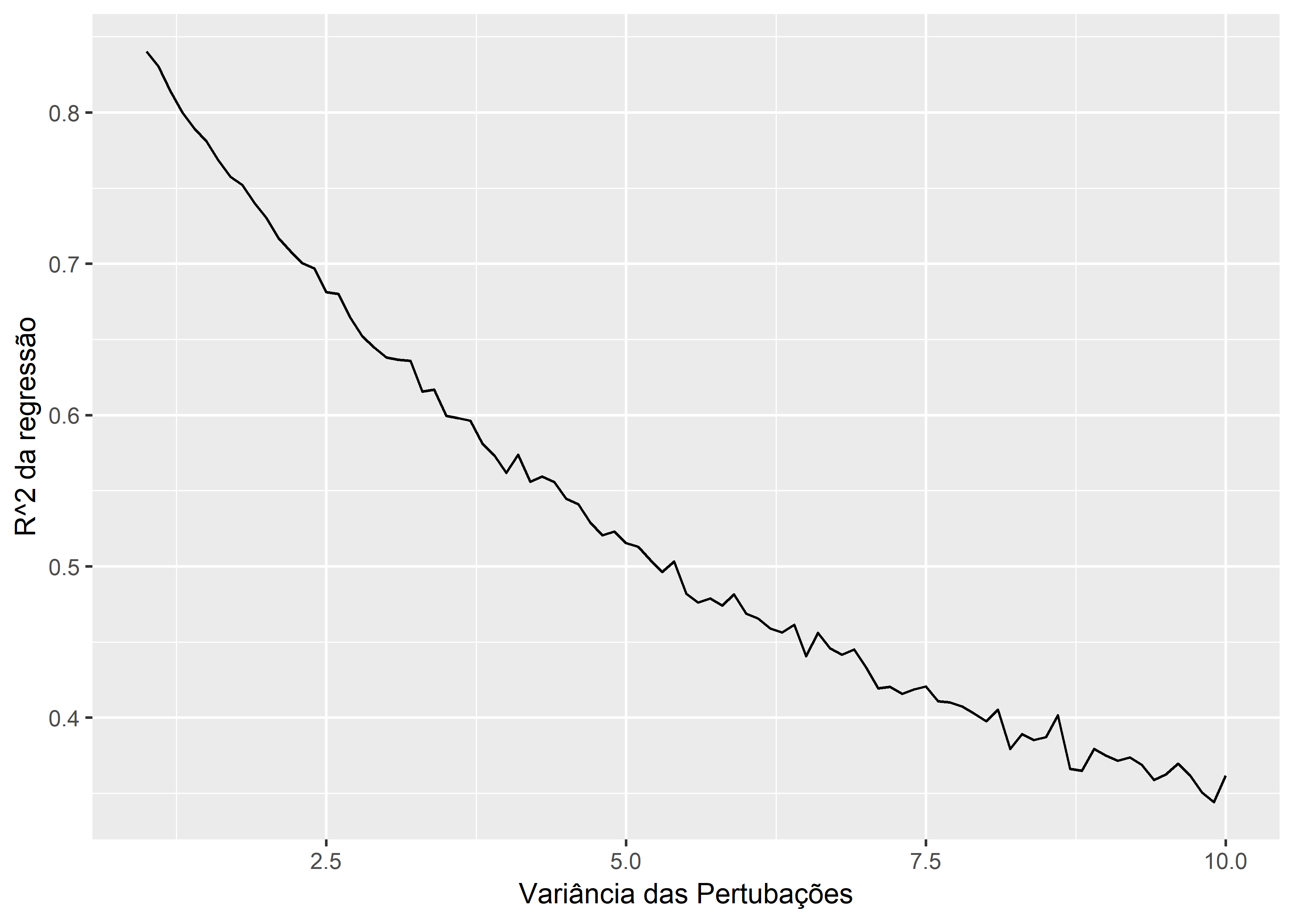
E como o estimador responde à variância das pertubações? Mais ainda, será que nossa regressão perde poder explicativo?
variancias = seq(1, 10, by = 0.1)
errequadrados = vector()
for(i in 1:length(variancias)) {
u = rnorm(n = m,
sd = sqrt(variancias[i])) # pertubações aleatórias com distribuição u ~ N(0,sigma)
Y = 5 + 0.8*X + u
dados = data.frame(explicada = Y,
explicativa = X)
modelo = lm(Y ~ X, # fórmula do modelo a ser estimado
data = dados) # data.frame em que estão as variáveis
errequadrados[i] = summary(modelo)$r.squared
}
grafico = data.frame(explicada = errequadrados,
explicativa = variancias)
grafico %>%
ggplot(aes(y = explicada,x = explicativa)) +
geom_line() +
ylab("R^2 da regressão") +
xlab("Variância das Pertubações")