Uma introdução à Cross Validation

Cross Validation (traduzido as vezes como Validação Cruzado e abreviado como CV) é um método bastante comum em Machine Learning para selecionar parâmetros ou hiperparâmetros. Eu já usei em outro post para o blog em que eu falei de LASSO, onde tinhamos que selecionar o parâmetro de penalização \(\lambda\).

A ideia do Cross Validation é simples: pegue seu conjunto de dados e divida em k blocos de tamanho igual (ou o mais igual possível se o número de observações não for um múltiplo de k). Estime o seu modelo para um certo número de parâmetros que são razoáveis em um bloco e veja qual a perda em alguma métrica (Erro Quadrático Médico, Erro Absoluto Médio, você escolhe) para os dados nos outros k-1 blocos. Faça isso para todos os blocos. A imagem abaixo ilustra a ideia (não é nenhuma obra de arte) para 5 blocos: a linha preta representa o conjunto de dados e as linhas vermelhas separam os blocos do Cross Validation. T indica que usamos aquele bloco numa dada iteração para “treinar” (ou estimar) o modelo e V que usamos aquele bloco para avaliar o desempenho do modelo. O modelo selecionado é o que performa melhor na média de todos os blocos.

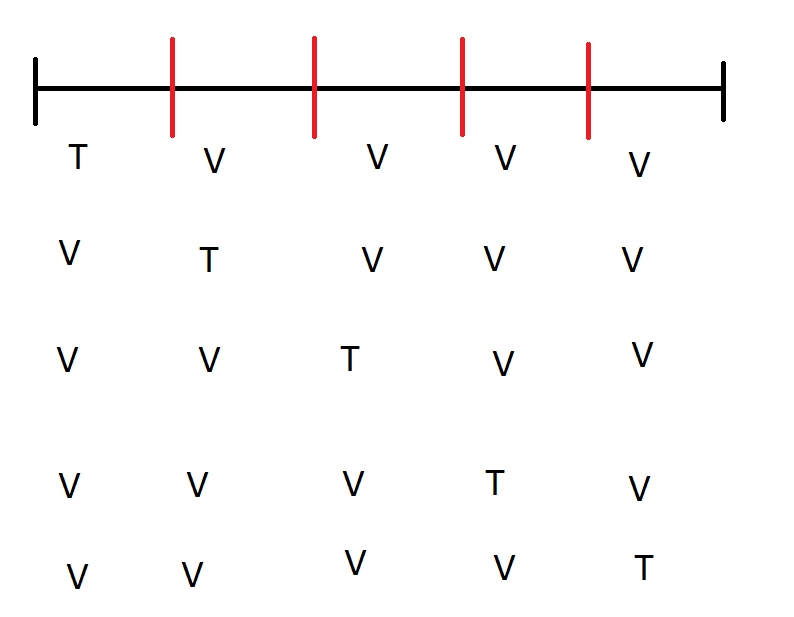
Veja que temos bons motivos para não usar o mesmo bloco que usamos para estimar o modelo para avaliar o modelo: dado o valor do parâmetro escolhido, em geral o algoritmo vai tentar escolher o melhor modelo para os dados. Nosso interesse é saber a performance do modelo em geral. Isso é verdade para várias aplicações: nós queremos bons modelos que façam previsão para o futuro, não para dentro da nossa amostra; queremos modelos explicativos em economia que não tenham válida apenas para aquela amostra de pessoas/período do tempo, mas sim para situações genéricas (o que é chamado de validade externa); etc.

Como tudo na vida, existem problemas com Cross Validation:

1. É computacionalmente intensivo. Se fazemos k blocos e cada modelo leva t segundos para estimar, então temos \(tk\) de tempo para estimar. Se ainda decidimos estimar um último modelo usando o parâmetro escolhido por CV e a amostra toda, acabamos gastando \(t(k+1)\).

2. Se temos poucas observações, pode ser problemático deixar de fora um pedaço da amostra na hora de estimar. Com uma amostra de 100 e 5 blocos, teremos blocos de 20 observações. Um modelo com 10 variáveis nos deixaria com 10 graus de liberdade.

3. Talvez mais importante, o processo requer que os dados sejam independentes: uma estrutura de depedência temporal não permite embaralhar os dados de qualquer forma, por exemplo. Felizmente existem algumas maneiras de fazer Cross Validation que levam isso em conta - que eu não irei explorar por este ser um post introdutório ao assunto.

Vamos ilustrar o Cross Validation para o parâmetro de regularização \(\lambda\). Veja que glmnettem um comando interno que faz isso automaticamente, o cv.glmnet, mas como o meu propósito é ilustrativo, eu implemento na mão: vamos gerar um modelo com 50 variáveis, 1000 observações, e as 10 primeiras são relevantes com coeficiente igual a 1 e o resto irrelevante:

X <- matrix(rnorm(50*1000),ncol=50)
betas <- c(rep(1,10),rep(0,40))
y <- X%*%betas + rnorm(1000)

O código que vai escolher o \(\lambda\) vai primeiro quebrar a amostra em 5 pedaços e depois fazer um for para estimar o modelo em cada um dos pedaços e testar a capacidade preditiva de cada um. Veja que precisamos usar os dados inteiros: não podemos misturar y[1] com x[10,], por exemplo. Para escolher os blocos, eu vou mandar o R fazer um sample de números 1:número de observações e quebrar isso em cinco blocos:

dados <- cbind(y,X)

valores_cv <- sample(1:1000,size = 1000,replace = F)

Veja que se eu deixar o glmnet escolher o lambda automaticamente em cada replicação do CV, ele vai escolher dependente dos dados e não poderemos comparar qual é o melhor. Então eu faço uma primeira passagem do glmnet por todo os dados com o objetivo de escolher um conjunto de lambdas que vai ser testado (isso é igual ao que o cv.glmnetfaz, diga-se de passagem)

tic()

modelo <- glmnet(X,y)
lambdas <- modelo$lambda

lambda_sel <- rep(0,5)

for(i in 1:5){
  amostra <- valores_cv[(1:200)+200*(i-1)]
  dados_train <- dados[amostra,]
  dados_vali <- dados[-amostra,] 
  modelo_cv <- glmnet(dados_train[,2:ncol(dados_train)],dados_train[,1],lambda = lambdas)
  x_aux <- cbind(1,dados_vali[,2:ncol(dados_vali)])
  u <- dados_vali[,1] - x_aux%*%coef(modelo_cv)
  ssr <- colSums(u^2)
  sel_indice <- which.min(ssr) #indice de qual modelo foi melhor
  lambda_sel[i] <- lambdas[sel_indice]
}

modelo_final <- glmnet(X,y,lambda = mean(lambda_sel))

tempo <- toc()

## 0.121 sec elapsed

tempo <- tempo$toc - tempo$tic

(A sugestão de usar o tictoc para pegar o tempo foi do Pedro). O tempo de execução é até bastante rápido, ficando em 0.121 segundos. Vamos fazer um plot dos coeficientes escolhidos:

plot(coef(modelo_final)[-1], ylab = " ")

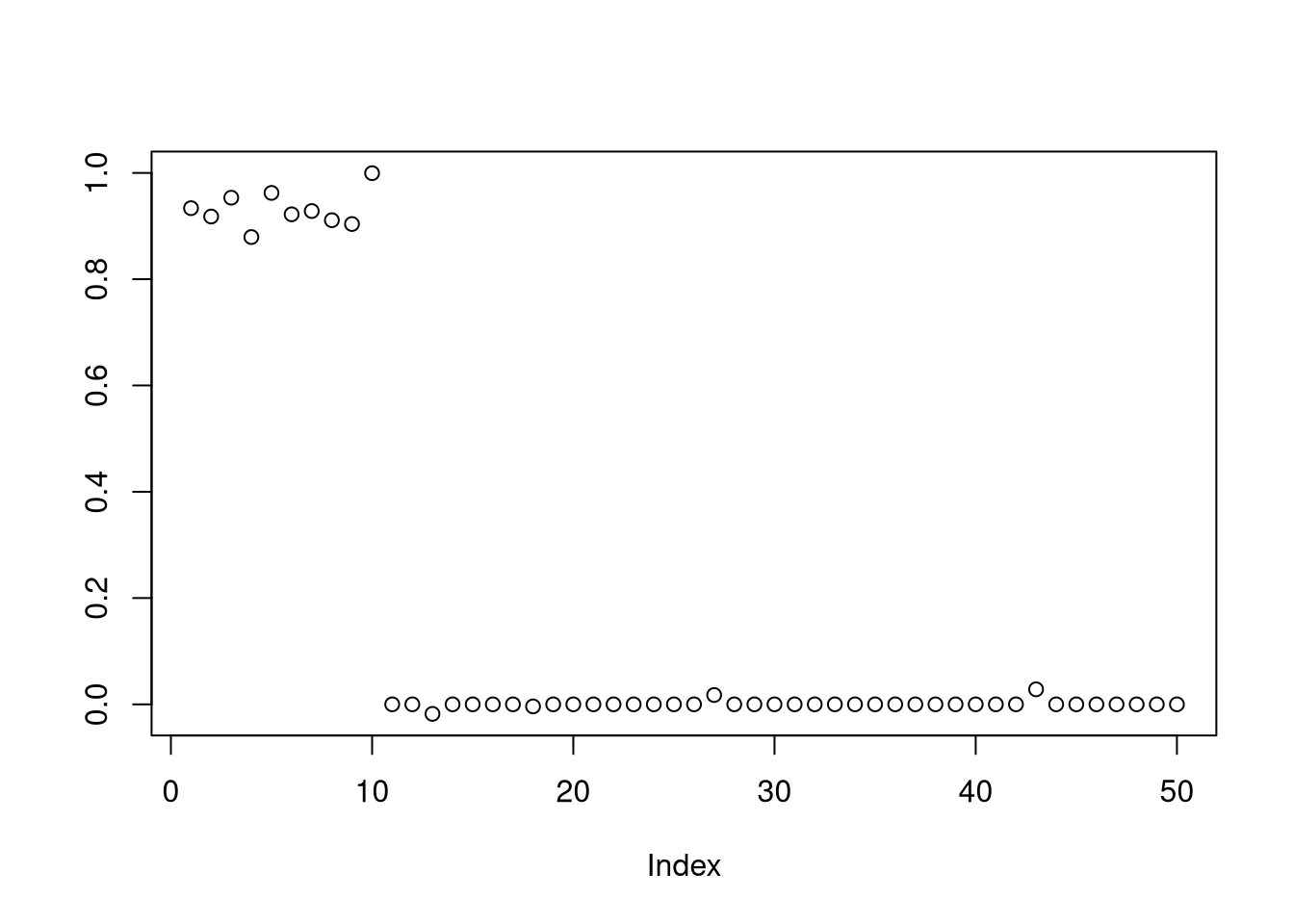
Aparentemente o cross validation conseguiu recuperar quase todos os coeficientes corretos. Vamos testar:

teste1 <- mean(coef(modelo_final)[2:11] !=0)
teste2 <- mean(coef(modelo_final)[12:51] == 0)
teste <- ifelse(teste1 + teste2 ==2,1,0)

tabela <- c(teste1,teste2,teste)*100
names(tabela) <- c("Não Zeros certos", "Zeros Certos", "Modelo Certo?")

knitr::kable(tabela,caption = "Todos os valores em porcentagem")

Veja que obviamente não podemos avaliar a qualidade do Cross Validation com base em uma única simulação. Nosso objetivo aqui é ilustrar a técnica. No post de LASSO e em post futuro sobre um irmão do LASSO, eu discuto a qualidade do CV para selecionar o parâmetro de regularização.

Veja que Cross Validation não é usado apenas para escolher parâmetros de regularização do LASSO: quase qualquer hiperparâmetro de um modelo pode ser selecionado por cross validation. Árvores de regressão são outro contexto em que o Cross Validation é usado, por exemplo. Mas como de praxe, existem hipóteses das quais o CV parte. Uma delas é independência entre as observações, que é inadequada em muitos casos com dados econômicos.

Com esse (relativamente) curto post, eu espero que o leitor tenha o mínimo de noção como o Cross Validation é usado e quais as suas limitações. Este post é introdutório: diversos livros falam de Cross Validation, inclusive o Elements of Statistical Learning, que você pode baixar de maneira 100% legal pelo link. Cross Validation é muito comum em técnicas de Machine Learning e portanto serão frequentes no blog.