Time Domain Iteration: mais programação dinâmica (Ou: como modelar firesales)

Em posts anteriores eu apresentei uma maneira de resolver o problema:

\[\max \displaystyle \sum_{t=0}^\infty \beta^t u(C_t) \text{ sujeito a uma restrição orçamentária}\]

O método que eu apresentei se valia de reescrever o problema como um problema recursivo usando a função valor, um método que também recebe o nome de Bellman Operator, devido a Richard Bellman, o desenvolvedor original da ideia. O método também é chamado de value function iteration, já que a cada iteração do algoritmo nós mudamos a aproximação da função valor.

No primeiro post da série eu dei a deixa que nós podiamos reescrever o problema usando La Grange e tirar as condições de primeira ordem e isso gerava um problema com infinitas variáveis a serem escolhidas, os valores de \(C_t\) para cada período do tempo. Para deixar o problema bem concreto, vamos voltar ao problema que eu abordei originalmente, que eu repito aqui:

\[\max_{\{C_t,K_{t+1}\}_t} \displaystyle \sum_{t=0}^\infty \beta^t u(C_t) \text{sujeito a }k_{t+1} = (1-\delta)k_t + y_t - C_t\]

Onde \(\delta\) é a taxa de depreciação do capital, \(y_t\) é uma função de produção que depende do capital. Podemos escrever isso como um La Grangeano onde a restrição orçamentária de cada período tem um multiplicador \(\lambda_t\) associado:

\[\mathcal{L} = \sum_{t=0}^\infty \beta^t u(C_t) - \lambda_t(k_{t+1} - (1-\delta)k_t - y_t + C_t)\]

Nós podemos proceder como se esse problema não envolvesse infinitos controles e encontrar a condição de primeira ordem. Veja que nós temos duas variáveis a serem escolhidas, \(k_{t+1}\) e \(C_t\), que são amarradas pela restrição. Reescreva a restrição como \(C_t = (1-\delta)k_t + y_t(k_t) - k_{t+1}\) e substitua no problema para obter o problema de maximização sem restrição:

\[\max_{\{k_{t+1}\}_t} \sum_{t=0}^\infty \beta^t u((1-\delta)k_t + y_t(k_t) - k_{t+1})\]

Teremos como condição de primeira ordem (famosamente “deriva e iguala a zero”) para um dado período \(t\):

\[-\beta^t u'(C_t) + \beta^{t+1} u'(C_{t+1})(1-\delta+y_t'(k_{t+1}))=0\]

(Abra o somatório para t e t+1 se você não entendeu de onde saiu isso). Podemos simplificar:

\[u'(C_t) = \beta u'(C_{t+1})(1-\delta+y_t'(k_{t+1}))\]

Veja que essa é a equação de Euler, e que o problema que nós resolvemos nos posts anteriores precisa respeitar isso (é uma condição necessária, mas não suficiente). Mas nós não usamos ela em ponto algum. Seria possível construir um algoritmo que resolve o problema partindo dessa equação? E isso seria vantajoso de alguma maneira?

As respostas são sim e sim. Vamos primeiro ao algoritmo, que recebe variados nomes, inclusive time domain iteration ou Coleman Operator, em homenagem a Wilbur Coleman, que estudou esse problema a fundo. Enquanto no algoritmo anterior nós estipulavamos valores para a função valor, aqui nós vamos estipular valores para \(C_{t+1}\). Eis o passo a passo:

• Defina um grid para a variável de estado
• Comece com um chute inicial para como deve ser \(C_{t+1}\) para cada valor da variável de estado
• Itere até convergência os seguintes passos:
  1. Para cada valor da variável de estado, encontre o valor de \(C_t\) que faz \(u'(C_t) - \beta u'(C_{t+1})(1-\delta+y_t'(k_{t+1})) = 0\)
  2. Estabeleça uma nova função que relaciona a variável de estado a \(C_{t+1}\), baseado no valor que maximiza \(C_t\) na iteração anterior

Veja que a ideia aqui é basicamente “operar” usando os mesmos valores que resolvem a condição de primeira ordem para sempre. Uma solução do problema é alcançada quando \(C_t = C_{t+1}\). Por incrível que possa parecer, é mais uma aplicação do teorema de ponto fixo que o Pedro descreveu faz um tempo aqui no blog.

Veja que para o caso onde \(\delta = 1\), \(u(C_t) = \ln(C_t)\) e \(y_t = k_t ^\alpha\), o problema tem solução analítica. O código que implementa o problema e resolve no Julia segue abaixo:

using Interpolations
using Plots
using Roots
using Distributions

### Primeiro: caso com produção, utilidade log e função de produção Cobb Douglas
## Esse caso tem solução analítica, que é implementada abaixo

beta = 0.95
alpha = 0.65

grid_size = 300

iter = 15

k_grid = range(1e-5,8,length=grid_size) #grid para a variável de estado

uline(c) = 1/c
f(k) = k^alpha
fline(k) = alpha*k^(alpha-1)

c_val = zeros(grid_size,iter)
c_val[:,1] =  f.(k_grid)

for i in 2:iter
    for j in 1:grid_size
        foo_c = LinearInterpolation(k_grid,c_val[:,i-1],extrapolation_bc = Line()) #usando uma aproximação linear (por partes) para a função do consumo
        function g(c)
            y = f(k_grid[j])
            return uline(c) - beta*fline(y-c)*uline(foo_c(y-c))
        end
        c_val[j,i] = find_zeros(g,1e-10,f(k_grid[j]))[1] #resolvendo a equação de euler
    end
end

Observe que meu chute inicial é “consuma tudo o que foi produzido”, que é um chute factível mas improvável de ser a verdadeira política ótima. Veja ainda que eu coloquei apenas 15 iterações do algoritmo, um número extremamente baixo - especialmente se considerarmos que a solução analítica do problema é não linear na variável de estado, já que \(c_t = (1-\alpha \beta) y_t = (1-\alpha \beta) k_t^\alpha\). Vamos ver qual a diferença entre a solução numérica e a analítica:

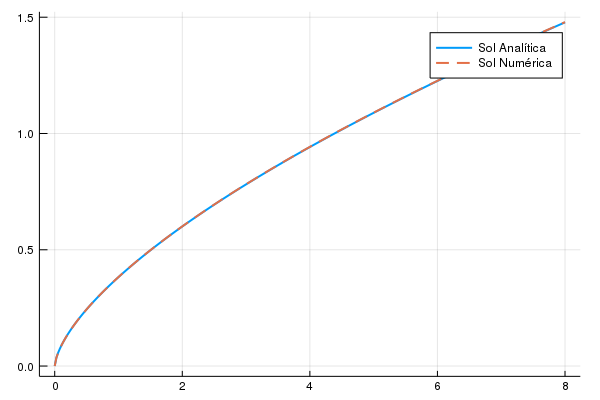
A olho nu, os dois são indistiguíveis. Vamos ver o que acontece quando usamos apenas 15 iterações do método da função valor. O gráfico a seguir apresenta a diferença entre os valores da regra de decisão analítica para cada um dos métodos de resolução:

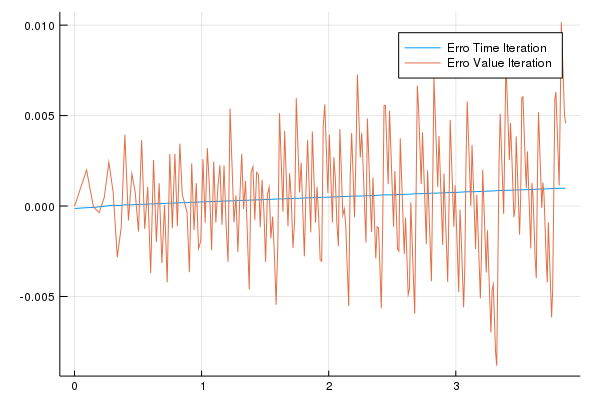
As diferenças são pequenas (0,01), mas veja que a diferença usando a time iteration é totalmente fora de escala com o método de value function iteration. O método apresento neste post tem ganhos claros sobre o método anterior, apesar de ser uma variação extremamente simples.

Mais existe uma razão extra para eu achar esse método interessante (e na verdade a razão pela qual eu aprendi ele em primeiro lugar): é fácil adaptar ele para situações na qual algumas vezes temos uma restrição que está ativa e em outras situações não. O exemplo simples disso requer um problema diferente que eu já ataquei aqui com programação dinâmica: suponha que, ao invés do agente ter acesso a uma tecnologia de produção que usa capital, ele recebe um salário, \(w_t\), que segue um processo aleatório (possivelmente até dependente no tempo!). O agente pode cobrar um único ativo, que paga uma taxa de juros fixa,\(r\). Além da restrição orçamentária, o agente também tem uma restrição a se endividar: às vezes o agente pode estar excessivamente endividado e a restrição a endividamento estar ativa; outras vezes o agente pode ter riqueza o suficiente que a restrição não esteja ativa. Eu vou escrever o problema formalmente matematicamente:

\[\max_{\{c_t,b_{t+1}\}_t} \sum_{t=0}^{\infty} \beta^{t} u(c_t) \text{ sujeito a}\\ (1+r)b_t + w_t = b_{t+1} + c_t \quad (2)\\ b_{t+1} > -\kappa w_t \quad (3)\]

A ideia de como adaptar o algoritmo e o formato da restrição foram retirados de (um pedaço) da tese de doutorado do Javier Bianchi. Lá ele apresenta uma justificativa para a restrição de envidamento como (3): se o sujeito “der o calote”, devido as leis, o credor só consegue obter uma fração \(\kappa\) do que devedor obtém .Para entender o algoritmo, vamos reescrever a equação (2) acima para colocar a \(c_t\) em evidência e substituir no \(c_t\) dentro da utilidade e reescrever tudo como um lagrangeano, obtendo:

\[\mathcal{L} = \sum_{t=0}^{\infty} \beta^{t} u((1+r)b_t + w_t - b_{t+1}) -mu_t(-b_{t+1} - \kappa w_t)\]

A única variável de controle é \(b_{t+1}\) e \(\lambda_t > 0\) fica claro que na condição de primeira ordem vai ser:

\[-u(c_t) + (1+r)\beta u(c_{t+1}) +\mu_t = 0 \therefore \mu_t = u(c_t) - (1+r)\beta u(c_{t+1})\]

Veja que, quando temos uma restrição em desigualdade, o seguinte tem que sempre valer:

\[\mu_t(b_{t+1} + \kappa w_t) = 0\]

Isso significa que das duas uma: ou a restrição vale com igualdade, e o termo entre parenteses é igual a 0; ou o multiplicador de la grange é igual a zero e a restrição não está ativa. Veja que juntando esse último fato com a condição de primeira ordem para este problema, nós temos que se a restrição de endividamento valer, então \(u(c_t) - (1+r)\beta u(c_{t+1}) >0\). E se a condição não valer, então \(\lambda_t = 0\) e a equação fica \(u(c_t) - (1+r)\beta u(c_{t+1}) = 0\). Isso nós dá uma maneira fácil de checar se a restrição está ativa ou não: veja se a equação de Euler vale com desigualdade. Se sim, estamos no caso em que a restrição está ativa. Senão, procedemos normalmente. Vamos escrever o passo a passo do algoritmo. Lembre-se sempre que começamos dando algum chute inicial para o formato da função consumo e temos que definir um grid para os valores do título e do salário, que são as nossas variáveis de estado:

1. Compute qual é o máximo de dívida disponível para esse período usando a equação (3). Esse valor vai ser \(b_{max}\)
2. Compute o quanto vai ser consumido se o agente pegar o máximo de dívida disponível usando o valor do passo anterior e (2). Chame esse valor de \(c_{max}\).
3. Compute o valor de \(u(c_{max}) - (1+r)\beta E(u(c(b_{max})))\). Se o valor for maior que 0, pule para o item 5
4. Encontre o valor que faz com que \(-u(c_t) + (1+r)\beta u(c(b_{t+1})) = 0\).
5. Salve o valor de \(c_t\)
6. Proceda até convergência

Veja que esse algoritmo é ligeiramente diferente do algoritmo do Bianchi em alguns pontos - e porque o problema que eu estou resolvendo aqui no blog é mais simples que o problema dele. Eu vou usar preferências log, que geram como derivada \(u'(c)=1/c\). Além disso eu vou adotar uma hipótese simplificadora de que a dotação só pode adotar 4 valores: 2,3,4,5, todos com a mesma probabilidade (0.25). Isso é porque nós vamos ter duas variáveis de estado, a quantidade de títulos e a renda no período - já que um pedaço fundamental do problema é a restrição de endividamento, que depende da renda. Vamos ao algoritmo em si:

beta = 0.96
r = 0.04
sigma = 2
kappa = 0.32

bond_grid_size = 200
y_grid_size = length(2:5)

y_grid = collect(2:5)
dist = DiscreteUniform(2,5)
prob = pdf.(dist,y_grid)

uline(c) = 1/c

iter = 50
bond_grid = range(-1.8,2,length=bond_grid_size)

cons = zeros(iter,bond_grid_size,y_grid_size)
cons[1,:,:] = [bonds + ys for bonds in bond_grid, ys in y_grid] #consome tudo o que tem hoje

i=2
err = 1  

#o algoritmo em si

while i <=iter&&err>1e-9 #enquanto a maior mudança na política for maior que 1e-9 o algoritmo. Ele para de qualquer forma se alcançar o número máximo de iterações
    foo_c = LinearInterpolation((bond_grid,y_grid),cons[i-1,:,:],extrapolation_bc = Flat()) #interpolando a função consumo
    for k in 1:y_grid_size
        b_aux = -kappa*y_grid[k] #o maximo de endividamento
        for j in 1:bond_grid_size
            c_aux = (1+r)*bond_grid[j] + y_grid[k] - b_aux # o consumo no máximo de endividamento
            teste = uline(c_aux) - beta*(1+r)*prob'*uline.(foo_c(b_aux,y_grid)) #aqui é o teste da etapa 3 do algoritmo
            if teste > 0 #eis a etapa 3
                cons[i,j,k] = max(c_aux,0)
            else
                function f(c) #etapa 4: vamos primeiro estabelecer uma função para a rotina do Julia buscar por zeros
                    bb = (1+r)*bond_grid[j] + y_grid[k] -c
                    uline(c) - beta*(1+r)*prob'*uline.(foo_c(bb,y_grid))
                end
                cons[i,j,k] = find_zeros(f,1e-8,(1+r)*bond_grid[j] + y_grid[k]+1)[1] #busca por um zero na equação de Euler e salva o valor que zera
            end
        end
    end
    global err = maximum(abs.(cons[i,:,:]-cons[i-1,:,:])) #qual a mudança máxima em valor absoluto entre as duas iterações?
    println("iteration",i,"error",err) #só nos informa da evolução do algoritmo
    global i = i+1
end

Vamos ver como é a função consumo na última iteração:

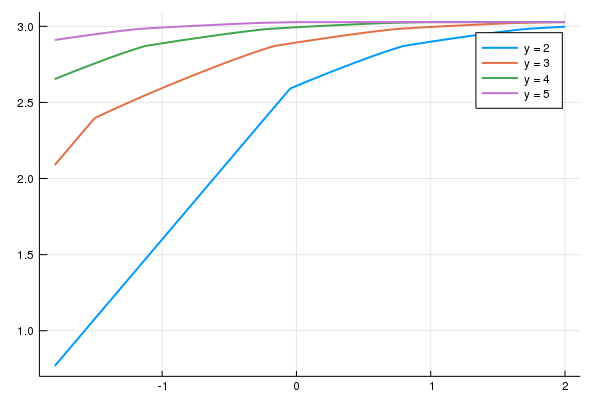
Veja que tem uma quebra ao redor do zero para o caso em que a dotação é mais baixa (y=2) e uma quebra parecida, mas bem mais a esquerda no caso y=3.

Um gráfico interessante que o Bianchi faz é ver como os títulos do próximo período dependem da quantidade de títulos hoje. Podemos fazer isso para cada nível de renda, mas é mais interessante para o valor mais baixo.

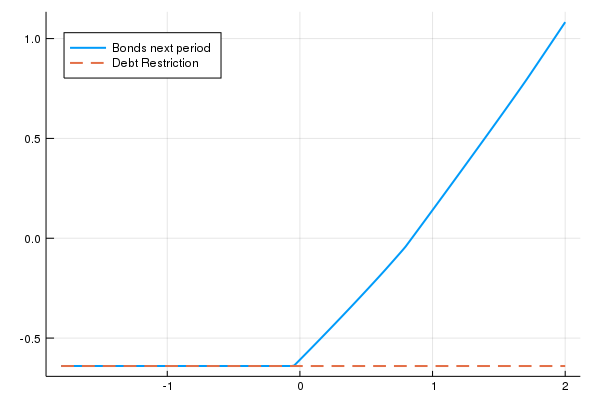
Veja que podemos ver exatamente os valores de título em que a restrição de endividamento está ativa. O caso dele é mais interessante porque ele coloca dois bens e o preço de um deles depende do ativo. Isso gera espaço para fire sales, o fenômeno em que o preço dos ativos cai, o que leva as pessoas a venderem o ativo para terem liquides e portanto o preço do ativo cai mais - uma das coisas observadas durante a crise financeira em 2008. É fácil adptar esse exemplo para permitir firesales, apesar de ter algumas etapas mais complicadas. O que eu vou fazer é seguir o exemplo do Bianchi (2011) mas simplificar a estrutura estocástica do problema: nós teremos dois bens agora, x e y. A nova função de utilidade é: \(\alpha \ln(x) + (1-\alpha)\ln(y)\) (uma Cobb Douglas) e o problema a ser resolvido é:

\[\max \sum_{t=0}^\infty \beta^t (\alpha \ln(x) + (1-\alpha)\ln(y)) \text{ sujeito a}\\ x_t + p_y y_t +b_{t+1} = (1+r)b_t + \omega^x_t + p_y \omega^y_t\\ b_{t+1} > -\kappa(\omega^x_t + p_y \omega^y_t)\]

Onde \(\omega^x_t\) e \(\omega^y_t\) são as dotações de x e y no períod t, respectivamente. Veja que como temos dois bens, normalizados o preço do bem \(x\) para ser igual a 1. Veja que o preço do bem \(y\) dependem não só das dotações agregadas como da quantidade de títulos que o agente mantém. Nós esperaríamos que um agente mais endividado vai estar mais interessado em vender o bem e com menos capacidade de comprar o bem: logo o preço do bem deve crescer conforme o agente fica mais rico. Veja que o agente não internaliza esse efeito de quantidade de títulos no preço do bem, o que gera uma “externalidade pecuniária”.

Veja que para facilitar a vida eu vou impor que em equilíbrio \(y_t = w^y_t\) - pense que isso pode ser a produção doméstica do agente (ou no caso de uma economia aberta, a produção de non tradables). Isso faz com que em equlíbrio, \(x_t + b_{t+1} = (1+r)b_t + \omega^x_t\).

Um outro detalhe técnico é que como temos dois bens e eu vou fazer com que ambos sigam uma distribuição discreta uniforme entre 2 e 5 (ou seja, P(2) = P(3) = P(4) = P(5) = 0.25), nós teremos 16 estados possíveis - e nesse caso a probabilidade de cada estado é \(0.25 \times 0.25 = 0.0625\) - e precisamos fazer todas as combinações possíveis de dotações dos dois bens (bem x com dotação 1 e bem y com dotação 1, bem x com dotação 1 e bem y com dotação 2, bem x com dotação 2 e bem y com dotação 1 etc). Felizmente a função Product do pacote Iterators (que já vem com o Julia) faz isso para gente. Só precisamos reorganizar porque ele devolve um objeto tuple e queremos arrumar isso em um array. Isso deixa o código um pouco mais indigesto, mas a ideia geral é igual ao do código anterior.

O código em si:

beta = 0.96
r = 0.04
sigma = 2
kappa = 0.32
alpha = 0.5

bond_grid_size = 200
y_grid_size = length(2:5)
x_grid_size = length(2:5)

y_grid = collect(2:5)
x_grid = collect(2:5)
dist = DiscreteUniform(2,5)
prob_y = pdf.(dist,y_grid)
prob_x = pdf.(dist,x_grid)

endow_aux = reshape(collect(Iterators.product(x_grid,y_grid)),16,1)
endow = zeros(16,2)

for i in 1:16
    endow[i,1] = endow_aux[i][1]
    endow[i,2] = endow_aux[i][2]
end

prob = repeat([prob_x[1]*prob_y[1]],16)

uline(c) = alpha/c
p(c,y) = (1-alpha)/alpha*c/y

iter = 50
bond_grid = range(-1,2,length=bond_grid_size)

cons = zeros(iter,bond_grid_size,x_grid_size,y_grid_size)
cons[1,:,:,:] = [bonds + xs for bonds in bond_grid, xs in x_grid,ys in y_grid] #consome tudo o que tem hoje

py = zeros(iter,bond_grid_size,x_grid_size,y_grid_size)
py[1,:,:,:] .= 1

i=2
err = 1

while i <=iter&&err>1e-9 #enquanto a maior mudança na política formaior que 1e-9 o algoritmo. Ele para de qualquer forma se alcançar o número máximo de iterações
    foo_c = LinearInterpolation((bond_grid,y_grid,x_grid),cons[i-1,:,:,:],extrapolation_bc = Flat()) #interpolando a função consumo
    for k in 1:16
        index_x = findfirst(x_grid .== endow[k,1])
        index_y = findfirst(y_grid .== endow[k,2])
        for j in 1:bond_grid_size
            b_aux = -kappa*(x_grid[index_x] + py[i-1,j,index_x,index_y]*y_grid[index_y]) #o maximo de endividamento
            c_aux = (1+r)*bond_grid[j] + x_grid[index_x] - b_aux # o consumo no máximo de endividamento
            teste_aux = prob'*reshape(uline.(foo_c(b_aux,x_grid,y_grid)),16,1)
            teste = uline(c_aux) - beta*(1+r)*teste_aux[1] #aqui é o teste da etapa 3 do algoritmo
            if teste > 0 #eis a etapa 3
                cons[i,j,index_x,index_y] = max(c_aux,0)
                py[i,j,index_x,index_y] = p(cons[i,j,index_x,index_y],y_grid[index_y])
            else
                function f(c) #etapa 4: vamos primeiro estabelecer uma função para a rotina do Julia buscar por zeros
                    bb = (1+r)*bond_grid[j] + x_grid[index_x] -c
                    aux = prob'*reshape(uline.(foo_c(bb,x_grid,y_grid)),16,1)
                    uline(c) - beta*(1+r)*aux[1]
                end
                cons[i,j,index_x,index_y] = find_zeros(f,1e-8,(1+r)*bond_grid[j] + x_grid[index_x]+2)[1] #busca por um zero na equação de Euler e salva o valor que zera
                py[i,j,index_x,index_y] = p(cons[i,j,index_x,index_y],y_grid[index_y])
            end
        end
    end
    global err = maximum(abs.(cons[i,:,:,:]-cons[i-1,:,:,:])) #qual a mudança máxima em valor absoluto entre as duas iterações?
    println("iteration",i,"error",err) #só nos informa da evolução do algoritmo
    global i = i+1
end

Vamos ver se o preço do bem y de fato cresce com a quantidade de títulos:

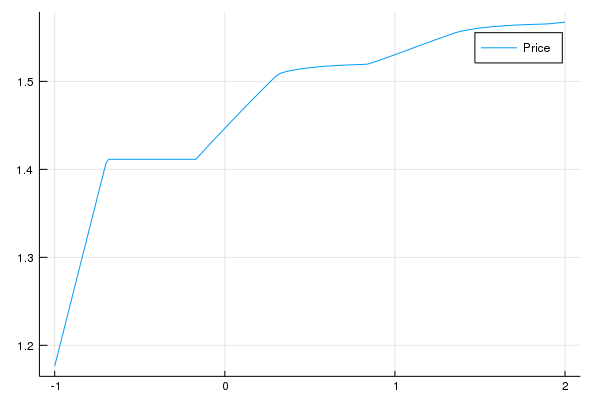
De fato cresce. Vamos ver o gráfico de qual a escolha de títulos amanhã dado os títulos hoje:

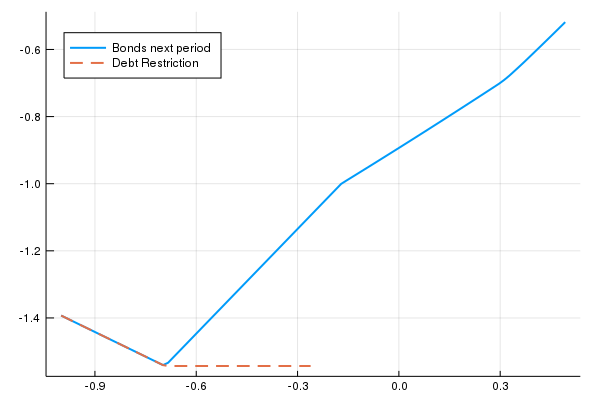
Veja que na ponta esquerda, quando a restrição está ativa, você vai escolher se endividar mais do que você se endividou hoje. Isso deprime os preços do bem y o que piora a restrição de endividamento do agente. Isso reduz o consumo dos agentes, o que deprime ainda mais os preços. O excesso de endividamento dos agentes leva a uma crise. Isso de forma alguma é uma ideia nova: Irving Fischer pós a crise de 1929 sugeriu esse mecanismo.

O post apresentou um método diferente de resolver problemas de programção dinâmica. Ele é mais eficiente e pode ser facilmente alterado para permitir restrições que ocasionalmente estão ativas. Isso é essencial para entender problemas chaves em macroeconomia, como restrições de endividamento. O formalismo matemático dá substância a ideia econônomica.

(Mais um post que o Sargent escreveu antes de mim e melhor (obviamente), mas em inglês. Imitação é a mais forma mais sincera de admiração. A outra fonte é, obviamente, o artigo do Bianchi)