Stranger things: Distribuição exata de IV em um exemplo extremamente simples
Esse post é uma consequência direta de um paper citado pelo Marcelo Medeiros em aula. Agradeço a referência
Variáveis instrumentais (IV) são bastante utilizadas em economia para resolver o problema de endogenidade. Nós temos teoria assintótica para IV, que mostra que em condições bastante gerais IV converge. Mas a experiência mostra que IV pode ter um comportamento absolutamente aberrante, especialmente se você tem muitos instrumentos - curiosamente, um dos meus primeiros posts do blog foi sobre viés de IV com muitos instrumentos.
O post de hoje vai mostrar, analiticamente e através de simulações, que a distribuição do estimador de variáveis instrumentais pode ser bem aberrante. O modelo é extremamente simples (que é o que permite obter distribuição analítica). Eu vou fazer todas as continhas porque é um exercício bacana. Se você só quer ver “a mágica acontecer”, pule a seção entre “As contas”.
Nada aqui é original, mas o exemplo é tão fantasticamente simples e gera uma distribuição tão maluca para alguns parâmetros que vale o post. As referências estão no fim do post.
O setup é extremamente simples, temos apenas duas equações:
\[y = \beta{} x + u\\ x = y + \gamma{}z\]
Onde \(y,x,z\) são escalares. Podemos usar \(z\) como instrumento para identificar \(\beta\). \(u\) é um erro com distribuição normal e variância \(\sigma^2_u\).
As contas
Vamos escrever as equações acima de maneira a obter duas equações: uma que só depende de x e z e outra que só depende de y e z. Basta plugar uma dentro da outra e obter:
\[y = \beta{}(y + \gamma{}z) + u\\ x = \beta{}x + u + \gamma{}z\]
E depois de alguma álgebra, nós temos:
\[y = \frac{\beta{}\gamma{}}{1-\beta}z + \frac{u}{1-\beta}\\ x = \frac{u}{1-\beta} + \frac{\gamma{}}{1-\beta}z\]
Veja que se nós dividirmos o coeficiente de de z na primeira equação (de agora por diante \(\pi_{yz}\)) pelo coeficiente de z na segunda equação (\(\pi_{xz}\)), nós recuperamos \(\beta\). Isso é o resultado usual de estimação por variáveis instrumentais. Veja que podemos escrever esses coeficientes estimados por mínimos quadrados:
\[\pi_{yz} = \frac{1/n\sum_i y_i z_i}{1/n\sum z_i^2}\\ \pi_{xz} = \frac{1/n\sum_i x_i z_i}{1/n\sum z_i^2}\\\]
E portanto, o nosso estimador de \(\beta\) por IV é \(\pi_{yz}/\pi_{xz}\), e nós teremos:
\[\hat{\beta} = \frac{1/n\sum_i z_i y_i}{1/n\sum_i z_i x_i}\]
Vamos destrinchar cada um dos somatórios para obter tudo em função de \(\sum_i z_i^2\) e \(\sum_i z_i u_i\). Vou começar com o somatório de cima. Ambos vão envolver substituir as expressões que nós encontramos de y e x como função de z e u no somatório, que é um passo bastante comum quando queremos provar várias coisas usando estimadores:
\[\sum_i z_i y_i = \sum_i z_i \left(\frac{\beta{}\gamma{}}{1-\beta}z_i + \frac{u_i}{1-\beta}\right) = \frac{\beta{}\gamma{}}{1-\beta} \sum_i z_i^2 + \frac{1}{1-\beta} \sum_i z_i u_i = \frac{1}{1-\beta} \left(\beta{}\gamma{}\sum_i z_i^2 + \sum_i z_i u_i\right)\] E equivalentemente para \(\sum_i z_i x_i\):
\[\sum_i z_i x_i = \sum_i z_i \left(\frac{\gamma}{1-\beta} z_i + \frac{u_i}{1-\beta} \right) = \left(\frac{\gamma}{1-\beta} \sum_i z^2_i + \frac{1}{1-\beta} \sum_i z_i u_i \right) = \frac{1}{1-\beta} \left( \gamma \sum_i z_i^2 + \sum_i z_i u_i \right)\]
Dividindo um pelo outro vamos obter:
\[\hat{\beta} = \frac{\beta{}\gamma{}\sum_i z_i^2 + \sum_i z_i u_i}{\gamma \sum_i z_i^2 + \sum_i z_i u_i}\]
Vamos colocar \(\sum_i z_i u_i\) em evidência. Passe o denominador multiplicando e um pouco de álgebra:
\[\hat{\beta}\left(\gamma \sum_i z_i^2 + \sum_i z_i u_i\right) = \beta{}\gamma{}\sum_i z_i^2 + \sum_i z_i u_i\\ (\hat{\beta} -\beta) \gamma \sum_i z_i^2 = (1-\beta) \sum_i z_i u_i\\ \sum_i z_i u_i = \frac{(\hat{\beta} - \beta)\gamma \sum_i z_i^2}{1 - \hat{\beta}}\]
A grande sacada aqui é notar que a distribuição de \(\sum z_i u_i\) condicional a \(z\) é uma normal com variância \(\sigma^2 \sum _i z^2_i\), então podemos usar o resultado acima para fazer uma mudança de variável na distribuição normal. Caso vocês não lembrem (ou não saibam), segue o teoreminha:
Se \(y \sim g(y)\) (y distribuído com função de densidade g), e seja x = f(y), então \(x \sim g(f^{-1}(x)) \left|\dfrac{df}{dy}\right|\)
Ou seja, para encontrarmos a distribuição de \(x = f(y)\) quando conhecemos a distribuição de y, basta plugar a inversa na função dentro da função densidade e multiplicar pelo módulo da derivada.
Vamos começar computando a derivada :
\[\dfrac{\partial \sum_i z_i u_i}{\partial \hat{\beta}} = \frac{\gamma \sum_i z^2_i(1-\hat{\beta}) + (\hat{\beta} - \beta)\gamma \sum_i z^2_i}{(1-\hat{\beta})^2} = \frac{(1-\beta)\gamma \sum_i z_i ^2}{(1-\hat{\beta})^2}\]
Vamos escrever a função de densidade:
\[f\left(\sum_i z_i u_i\right) = \frac{1}{\sqrt{2\pi\sigma^2_u}} \exp\left(-\frac{-(\sum_i z_i u_i)^2}{2\sum_i z_i^2 \sigma^2_u}\right)\]
Vamos colocar \(\hat{\beta} - \beta\), a diferença do estimador de IV para o valor verdadeiro. Vamos escrever a distribuição de \(f(\hat{\beta}-\beta)\):
\[f(\hat{\beta}-\beta) = \left|\frac{(1-\beta)\gamma \sum_i z_i^2}{(1-\hat{\beta})^2}\right| \frac{1}{\sqrt{2\pi\sigma^2_u}} \exp\left(-\frac{-((\hat{\beta}-\beta)\gamma \sum_i z_i^2)^2}{2(1-\hat{\beta})^2 \sum_i z_i^2 \sigma^2_u}\right)\]
Nós podemos simplificar um pouco a expressão dentro do exponencial para:
\[\exp\left(-\frac{\gamma \sum_i z_i^2}{2\sigma^2_u}\left(\frac{\hat{\beta} - \beta}{(1-\hat{\beta})}\right)^2\right)\]
A distribuição
A distribuição do estimador é \(f(\hat{\beta}) = \frac{\lambda_n}{\sqrt{2\pi}\sigma_u}\frac{|1-\beta|}{(1-\hat{\beta})^2}\exp\left(-\frac{\gamma \sum_i z_i^2}{2\sigma^2_u}\left(\frac{\hat{\beta} - \beta}{(1-\hat{\beta})}\right)^2\right)\), onde \(\lambda_n = \gamma/n\sum_i z_i^2\). Veja que \(\lambda_n\) mede o quão forte é o instrumentos: isso depende tanto da variância do \(z\) (medido pelo \(\sum_i z_i^2\)) e do valor de \(\gamma\).
Vamos usar o R para olhar como é essa distribuição para diferentes valores de \(\lambda\), \(\beta\) e \(\sigma^2_u\). Veja que se \(\beta = 1\) o problema não vai ser bem definido. Eu vou começar com \(\lambda =1\) e vou fixar \(\sigma^2_u=1\) e \(\beta = 0.6\).
dist <- function(x,lambda,btrue,varu){
sqrt(lambda/(2*pi*varu))*abs(1-btrue)/(1-x)^2*exp(-lambda/(2*varu)*((x-btrue)/(1-x))^2)
}
xx <- seq(-1,2,by = 0.01)
yy <- dist(xx,1,0.6,1)
plot(xx,yy, type = "l")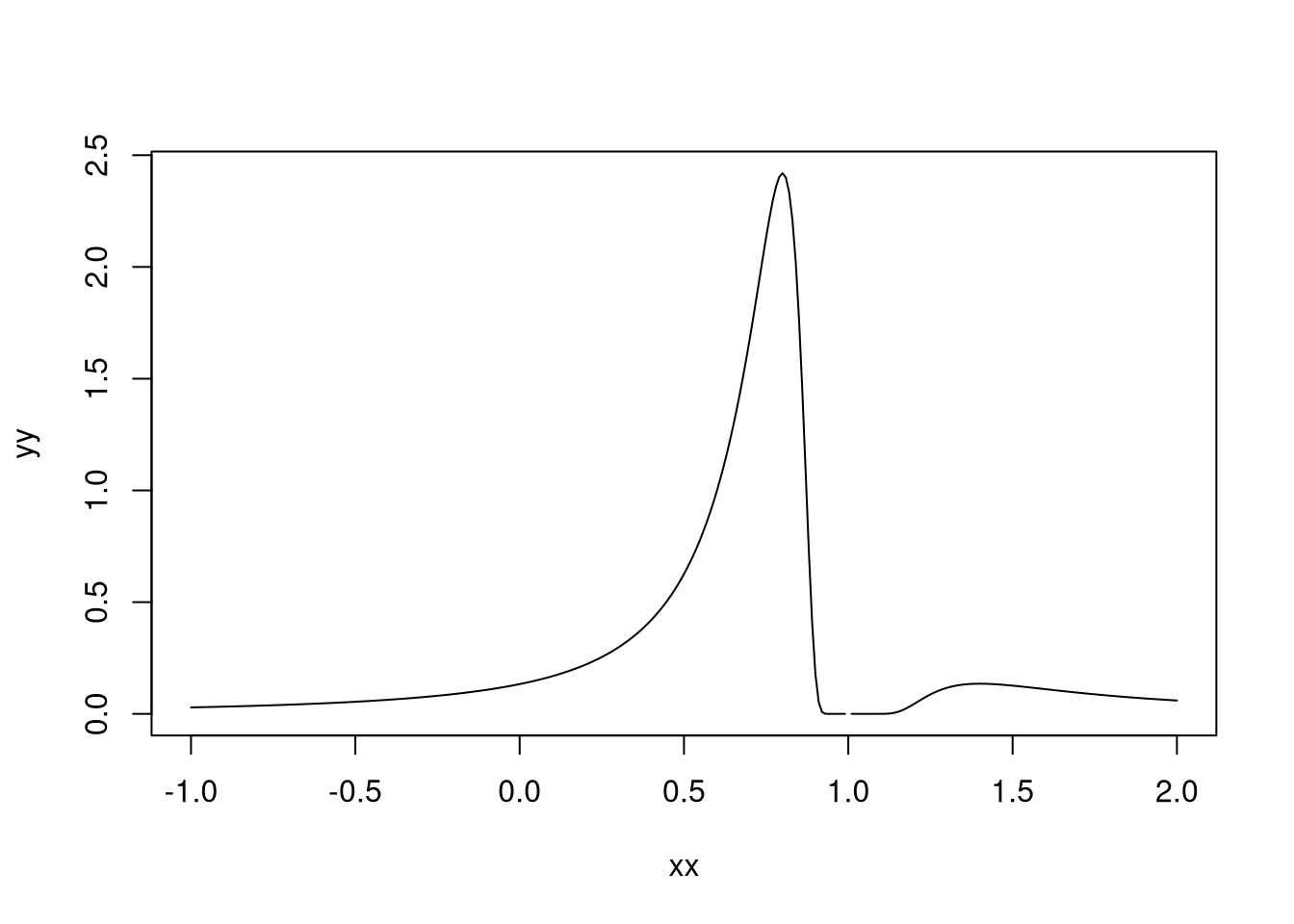
Veja que a distribuição é bem exótica e que ela não está definida quando a estimativa é 1. Ela tem um pico em 0.6 (como deveria ser) e tem um máximo local logo depois de 1, que pode gerar problemas para a estimação. O mais divertido é quando a gente reduz \(\lambda_n\). Eu vou colocar 0.1:
yy <- dist(xx,0.1,0.6,1)
plot(xx,yy, type = "l")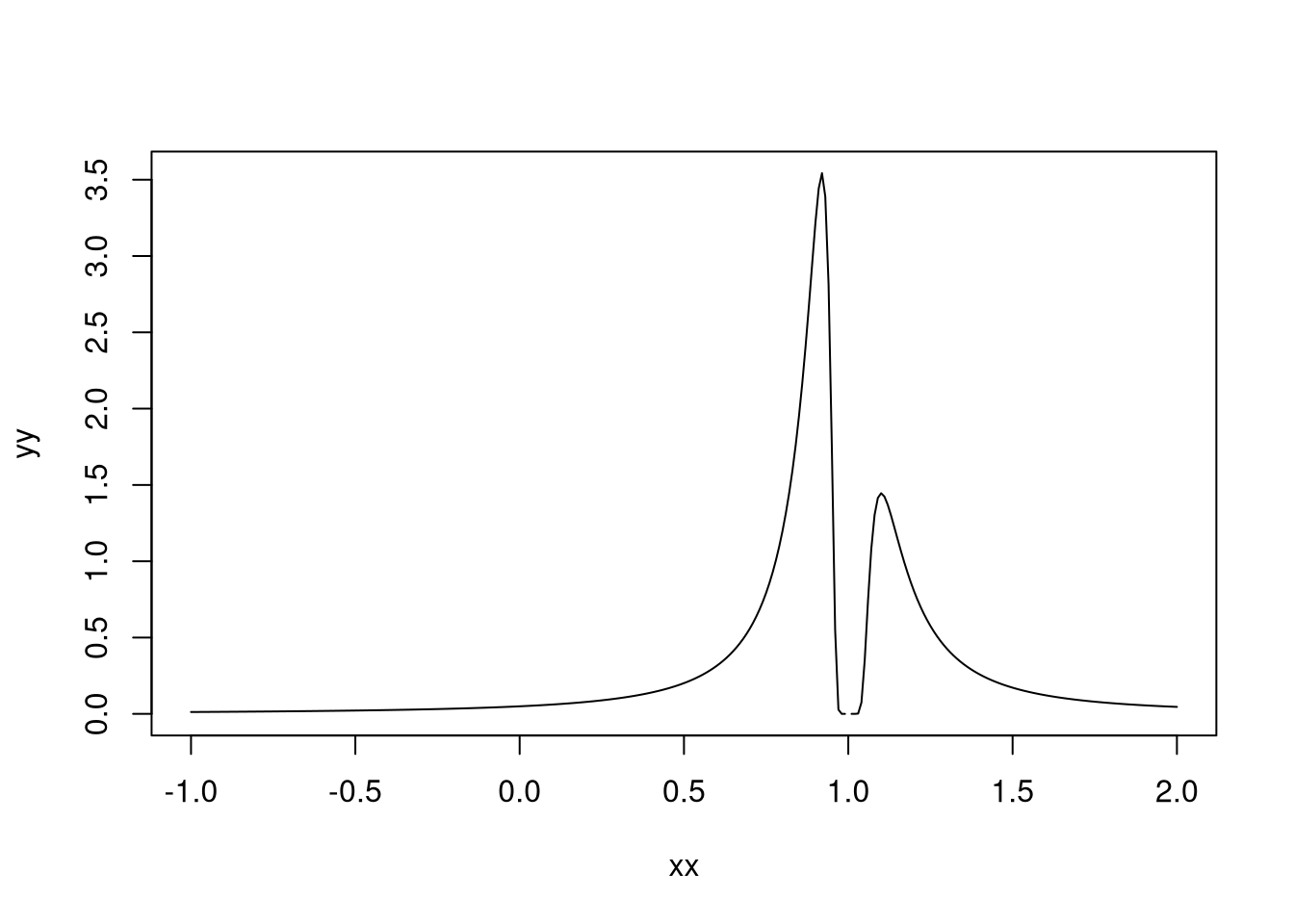
Agora a bimodalidade é evidente e preocupante. Podemos reduzir ainda mais \(\lambda_n\), para 0.01:
yy <- dist(xx,0.01,0.6,1)
plot(xx,yy, type = "l")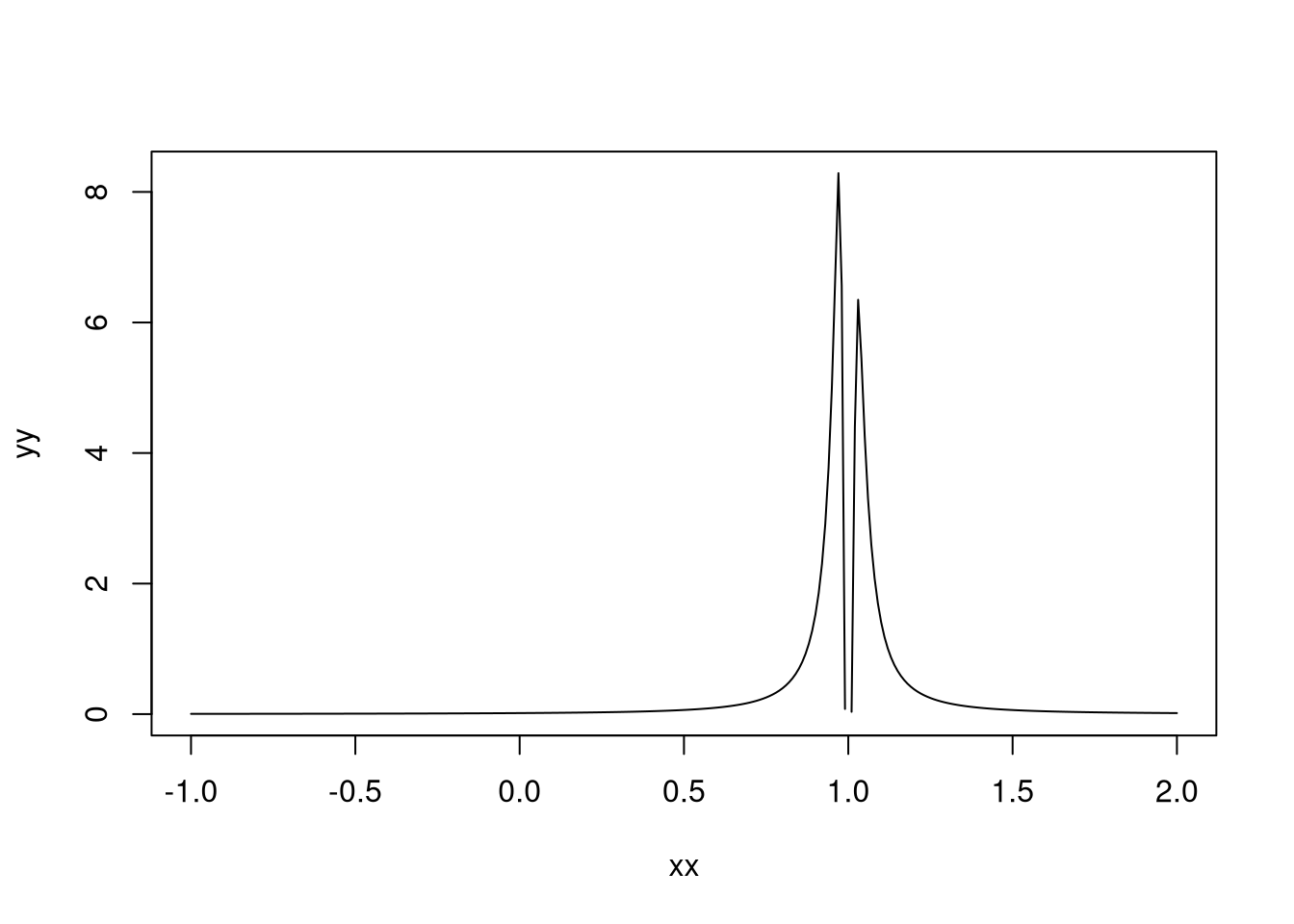
A distribuição é bimodal com duas modas perto de 1 - que não é o valor verdadeiro do parâmetro! Veja que mesmo mudando o valor verdadeiro do parâmetro e com um instrumento relativamente forte (\(\lambda_n = 1\)), a distribuição não tem moda no valor verdadeiro do parâmetro.
library(latex2exp)
yy <- dist(xx,1,0,1)
yy2 <- dist(xx,1,0.6,1)
plot(xx,yy2, type = "l")
lines(xx,yy,col=2)
legend("topleft", legend = c(TeX('$\\beta = 0.6$'),TeX('$\\beta = 0$')),lty=1,col=c(1,2))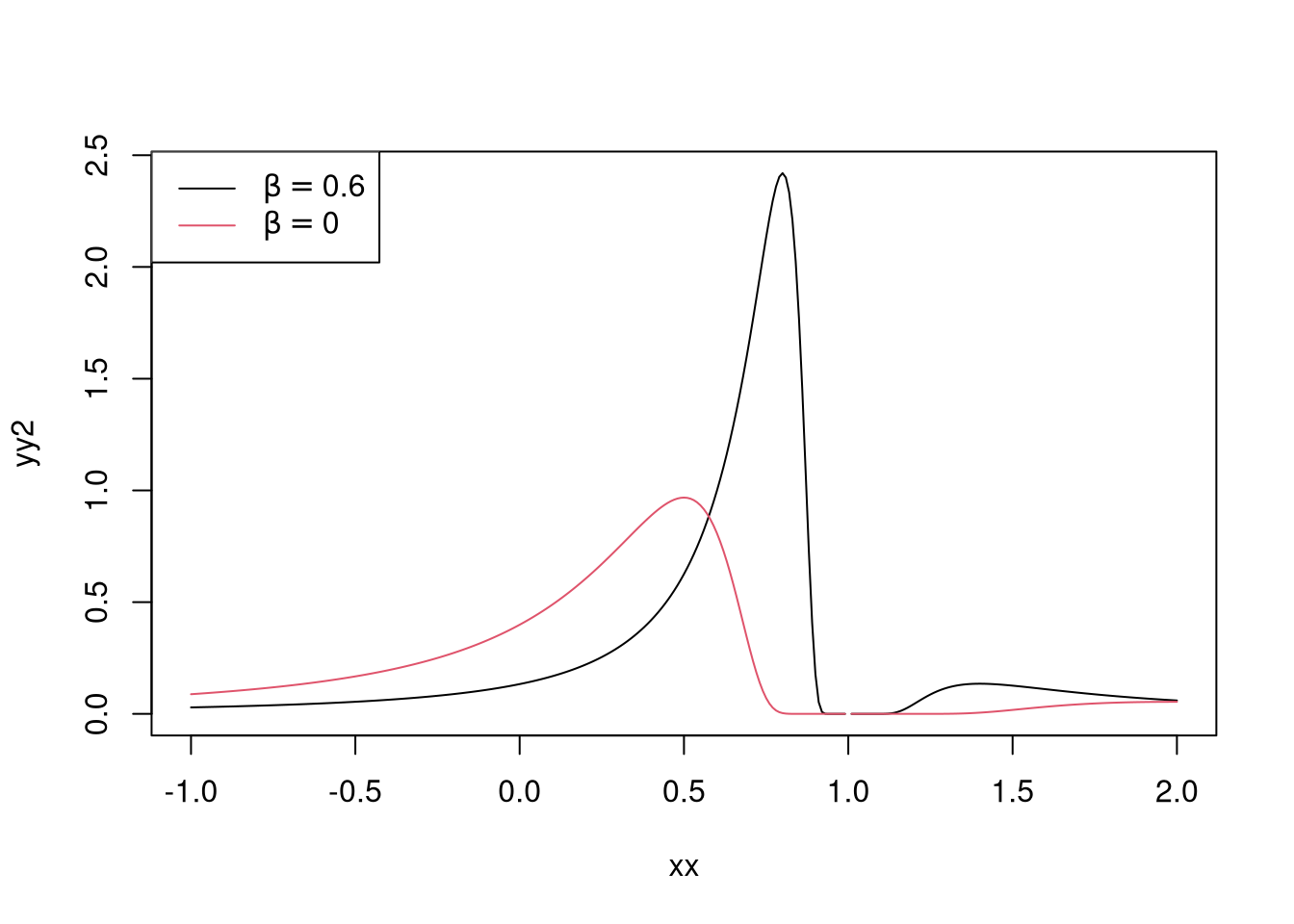
Os comandos LaTeX na legenda são processados pela função TeX(), do pacote latex2exp .Podemos fazer algumas simulações para testar isso. Eu vou escolher os parâmetros de maneira que o problema seja equivalente ao da distribuição que a gente usou e fazer amostras relativamente grandes:
library(AER)
set.seed(9076)
gama <- 1
beta <- 0.6
sigma_u <- 1
sigma_z <- 1
estimativas <- rep(0,1000)
for(i in 1:1000){
z <- rnorm(1000,sd = sigma_z)
u <- rnorm(1000,sd = sigma_u)
y <- 1/(1-beta)*(beta*gama*z+u)
x <- 1/(1-beta)*(u+gama*z)
modelo <- ivreg(y ~ x|z)
estimativas[i] <- coef(modelo)[2]
}
hist(estimativas, freq = F)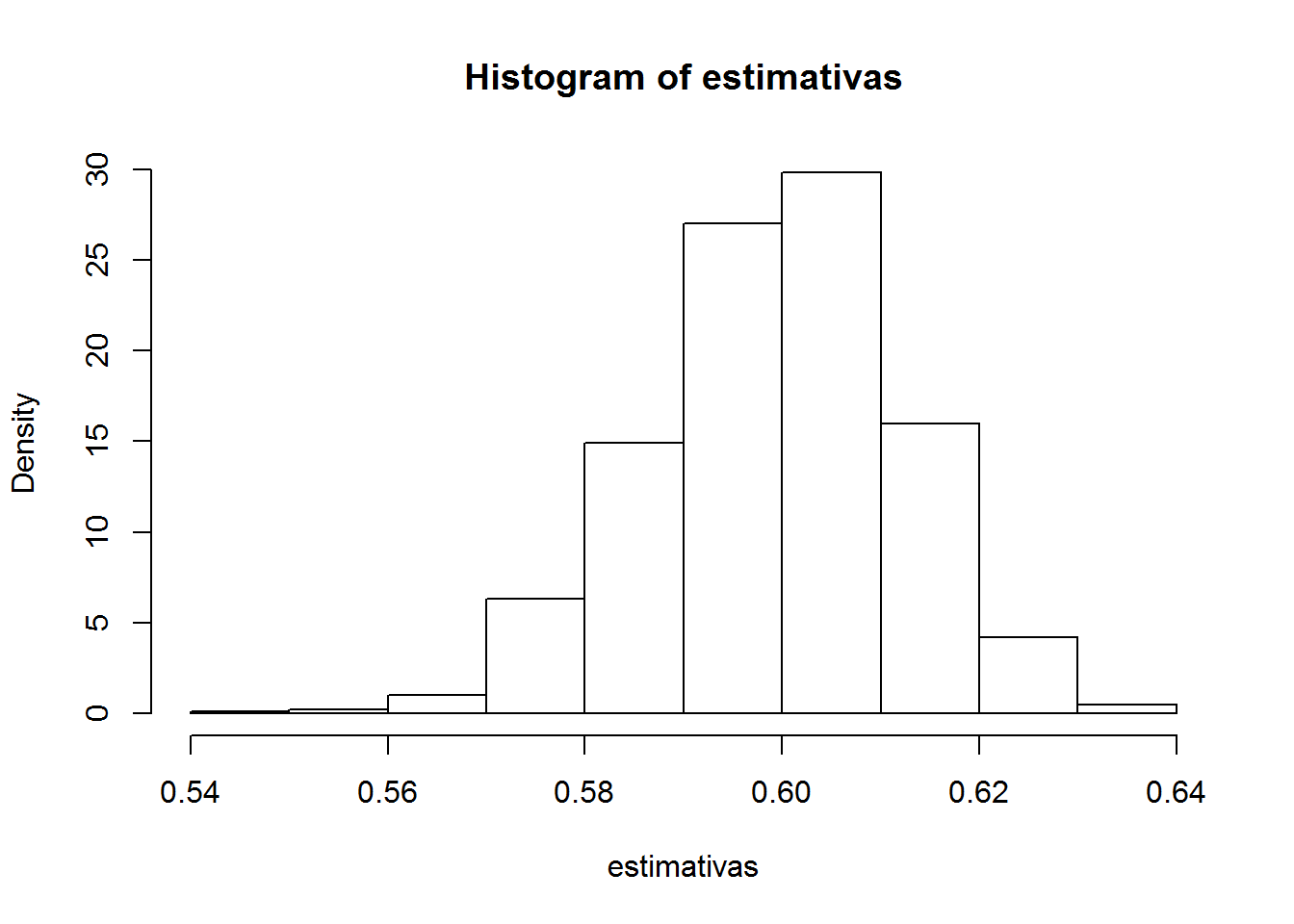
Apesar da distribuição do estimador ter um máximo local, o estimador até sobrevive bem. Vamos deixar o instrumento fraco reduzindo gama:
gama <- 0.1
beta <- 0.6
sigma_u <- 1
sigma_z <- 1
estimativas <- rep(0,1000)
for(i in 1:1000){
z <- rnorm(1000,sd = sigma_z)
u <- rnorm(1000,sd = sigma_u)
y <- 1/(1-beta)*(beta*gama*z+u)
x <- 1/(1-beta)*(u+gama*z)
modelo <- ivreg(y ~ x|z)
estimativas[i] <- coef(modelo)[2]
}
hist(estimativas, freq = F)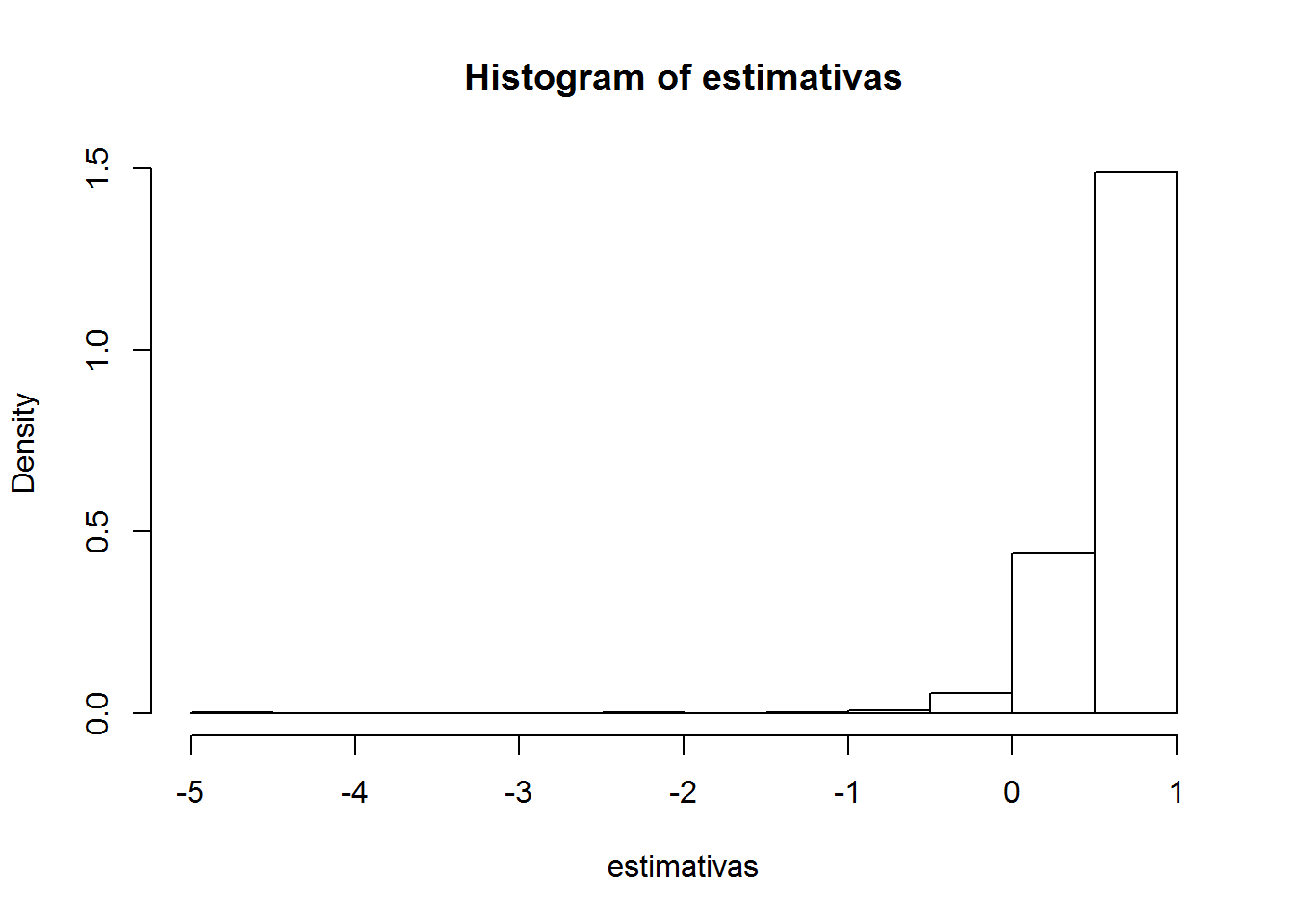
Como esperado, o resultado é catastrófico. A distribuição fica com toda a massa concentrada em 1, que sequer é o valor verdadeiro do parâmetro - na verdade, nesse ponto o estimador sequer está bem definido.
Esse post serve como um belo exercício de estatística - como obter uma distribuição exata de um estimador que estamos acostumados a pensar apenas em termos assintóticos - e serve como um alerta sobre o uso de variáveis instrumentais: mesmo em uma situação extremamente simples, nós podemos ter sério problemas. Isso depende do tamanho da amostra e do fatos dos instrumentos serem fracos - o que nem sempre é corretamente diagnosticado.
Referências
Some Further Results on the Exact Small Sample Properties of the Instrumental Variable Estimator, Charles R. Nelson and Richard Startz, Econometrica, 1990
A Remark on Bimodality and Weak Instrumentation in Structural Equation Estimation, Peter C.B. Phillips, Econometric Theory,2006