Sistemas dinâmicos II: Expectativas racionais
Há muito tempo atrás eu escrevi sobre Álgebra Linear e sistemas dinâmicos. Lá, eu falava de um caso em que o sistema era \(x_t = Ax_{t-1}\), onde \(x_t\) era um vetor e \(A\) tinha que ter autovalores menores que 1 em módulo para garantir a estabilidade do sistema. Apesar de ser um caso bem interessante, muitas vezes em economia nós temos que lidar com expectativas e assumimos expectativas racionais - que pode ser definida de várias maneiras, mas a mais intuitiva é pensar que agentes não cometem erros sistematicamente. Um caso “famoso” de expectativas racionais é a curva de Phillips novo keynesiana:
\[\pi_t = \beta E_t \pi_{t+1} + \kappa \tilde{y}_t\]
Onde \(\pi\) é a inflação e \(\tilde{y}_t\) é o hiato do produto.
Eu me perguntei durante muito tempo “como diabos você se livra dessa expectância?”. Com expectativas adaptativas, a resposta é bem simples: \(E_t(\pi_{t+1}) = \pi_t\). Para entender como funciona o caso com expectativas racionais, vamos dar um passo para trás e relembrar o passo a passo da equação em diferenças linear sem expectativas.
Suponha que você tem uma única equação, linear, \(x_t = \alpha x_{t-1}\). Podemos sempre iterar para trás e realizar substituição recursiva:
\[ x_t = \alpha x_{t-1}\\ x_{t-1} = \alpha{}x_{t-2}\\ x_{t-2} = \alpha x_{t-3}\\ ...\]
E substitua a última na penúltima, …, a terceira na segunda e a segunda na primeira para obter:
\[x_t = \alpha^tx_0\]
Onde \(x_0\) é uma condição inicial. Veja que se \(|\alpha| > 1\), o sistema explode. Caso contrário, o processo colapsa para zero. Normalmente, em economia, nós imaginamos que existe um choque aleatório \(\varepsilon_t\) e o sistema é \(x_t = \alpha x_{t-1} + \varepsilon_t\). Isso é só um AR(1) usual e a representação recursiva funciona da mesma forma, mas agora com um termo extra:
\[x_t = \alpha^t x_0 + \sum_{j=0}^t \alpha^j \varepsilon_{t-j}\]
Até aqui, nada de extremamente novo: esse é o ferramental usual de equações em diferenças. Agora, considere que nós temos uma única equação que tem uma expectativa (que assumimos ser racional):
\[E_t(y_{t+1}) = \lambda y_t\]
Veja que se \(y_t = y_{t+1} = 0\), a equação está no “estado estacionário”. Resscreva de maneira que \(y_t\) esteja em evidência:
\[y_t = \frac{1}{\lambda}E_t(y_{t+1})\]
O truque aqui é ao invés de iterar para trás, nós iteramos para frente:
\[ y_t = \frac{1}{\lambda}E_t(y_{t+1})\\ y_{t+1} = \frac{1}{\lambda}E_t(y_{t+2})\\ y_{t+2} = \frac{1}{\lambda}E_t(y_{t+3})\\ ... \]
Logo, substituição recursiva nos dá:
\[y_t = \frac{1}{\lambda^j}E_t(y_{t+j})\]
Se \(|\frac{1}{\lambda}| < 1\), então quando \(j \rightarrow \infty\), \(y_t = 0\). Veja que \(|\frac{1}{\lambda}| < 1\) é equivalente a \(|\lambda| > 1\).
O caso mais interessante é quando temos uma variável a mais no sistema, \(s_t\) - que pode ser determinística ou estocástica. Nossa equação se torna:
\[E_t(y_{t+1}) = \lambda y_t + s_t\]
(Veja que podíamos ter algum coeficiente na frente de \(s_t\)). Usando o mesmo truque que usamos acima, podemos reescrever isso:
\[y_t = \frac{1}{\lambda}(E_t(y_{t+1}) - s_t)\]
E iterando para frente:
\[y_t = \frac{1}{\lambda^j}E_t(y_{t+j}) - \sum_{k=0}^j \frac{1}{\lambda^k} E_t(s_{t+k})\]
Com \(j \rightarrow \infty\), obtemos \(y_t = -\sum_{k=0}^j \frac{1}{\lambda^k} E_t(s_{t+k})\).
Então para resolver equações em diferenças com expectativas, nós iteramos para frente e portanto exigimos que o coeficiente associado a \(y_t\) seja maior que 1.
Em um sistema de equações lineares, isso se reflete de maneira bem simples: antes, para termos estabilidade, todos os autovalores deveriam ser menores que 1. Agora, quando tivermos expectâncias, precisamos de 1 autovalor maior do que 1 para cada equação que depender da expectância da variável (isso não é sem alguns caveats técnicos). Isso é conhecido como condições de Blanchard Khan. Verificar as condições de Blanchard Khan é basicamente um exercício de contar quantos autovalores são maiores que 1 e quantos são menores que 1 e quantas equações dependem de expectativas e quantas não dependem. Veja que, seguindo a notação acima, teremos que escrever o sistema para termos:
\[E_t(x_{t+1}) = Ax_t + \epsilon_t\]
E checarmos os autovalores da matriz A: precisamos de ter o mesmo número de autovalores maiores que 1 que equações que dependem de expectativas; e mesmo número de autovalores menores que um do que equações sem expectativas. Alguns autores usam a equação ao contrário e colocam \(x_t\) do lado esquerdo e A acompanhando o vetor de expectativas. Nesse caso, as condições de Blanchard Khan se invertem.
Um exemplo
Vamos olhar o modelo Novo Keynesiano mais simples possível: ele tem uma equação IS intertemporal - como os agentes escolhem consumo hoje e amanhã dado a taxa de juros reais; uma curva de Phillips com expectativas; uma regra de política monetária que escolhe juros como função da inflação, um inflation target. Aqui vão as três equações:
\[ \pi_t = \beta E_t(\pi_{t+1}) + \kappa \tilde{y}_t\\ \tilde{y}_t = -\frac{1}{\sigma}(i_t - E_t(\pi_{t+1})) + E(\tilde{y}_{t+1})\\ i_t = \phi \pi_t + \varepsilon_t \]
Temos duas equações que dependem de expectativas e uma que não depende. Logo, precisamos de dois autovalores maiores que 1 em módulo e um menor que 1 em módulo. Vamos escrever do formato que eu coloquei acima, com todas as expectativas de um lado. Eu vou escrever o sistema na verdade como:
\[BE_t(x_{t+1}) = Cx_t + \varepsilon_t\]
E \(A = B^{-1}C\), logo vamos precisar inverter \(B\) (se ela for inversível). Temos:
\[\begin{bmatrix} \beta & 0 & 0\\ -1 & 1 & 1\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} E_t(\pi_{t+1})\\ E_t(\tilde{y}_{t+1})\\ i_t\\ \end{bmatrix} = \begin{bmatrix} 1 & -1 & 0\\ 0 & -\sigma & 0\\ \phi & 0 & 0\\ \end{bmatrix} \begin{bmatrix} \pi_t\\ \tilde{y}_t\\ i_{t-1}\\ \end{bmatrix} + \begin{bmatrix} 0 \\ 0\\ 1\\ \end{bmatrix} \varepsilon_t\]
Se você lembra dos cursos de macro (e aprendeu isso), o princípio de Tayor impõe que \(\phi > 1\) para o Banco Central controlar a inflação. Isso se traduz no sistema acima como “para o sistema satisfazer as condições de Blanchard Khan, \(\phi > 1\)”. É possível verificar isso analiticamente, mas vamos usar o R para isso. Vamos montar as equações, colocar alguns valores para os parâmetros e checar o número de autovalores maiores que 1. Primeiro, vamos checar que com \(\phi > 1\) temos o número de autovalores certos:
bet = 0.99
sig = 1
phi = 1.5
B = rbind(c(bet,0,0),c(-1,1,1),c(0,0,1))
C = rbind(c(1,-1,0),c(0,-sig,0),c(phi,0,0))
A = qr.solve(B)%*%C
eigen(A)## eigen() decomposition
## $values
## [1] -2.165909 1.165909 0.000000
##
## $vectors
## [,1] [,2] [,3]
## [1,] -0.2966180 -0.6109608 0
## [2,] -0.9326410 0.0942406 0
## [3,] 0.2054227 -0.7860316 1Temos dois autovalores maiores que 1 em módulo (um deles é um -2) e um menor que 1 em módulo (0). Logo, o sistema tem uma única solução (“as condições de Blanchard Khan são atentidas” usando os jargões de macro). Um pequeno detalhe: eu usei o comando qr.solve que faz a mesma coisa que o solve, mas é mais estável. Vamos testar vários valores para \(\phi\) e recuperar quantos autovalores são maiores que 1 em módulo:
bet = 0.99
sig = 1
phi_vals = seq(0,1.5, length.out = 100)
eigs_maior_que_um <- rep(0,length(phi_vals))
for(i in 1:length(phi_vals)){
phi = phi_vals[i]
B = rbind(c(bet,0,0),c(-1,1,1),c(0,0,1))
C = rbind(c(1,-1,0),c(0,-sig,0),c(phi,0,0))
A = qr.solve(B)%*%C
eigg <- eigen(A)
eigs_maior_que_um[i] <- sum(abs(eigg$values) > 1)
}
library(ggplot2)
dados <- data.frame("phi_vals" = phi_vals,"eigs" = eigs_maior_que_um)
g <- ggplot(dados, aes(phi_vals,eigs))
g + geom_line() + theme_bw() 
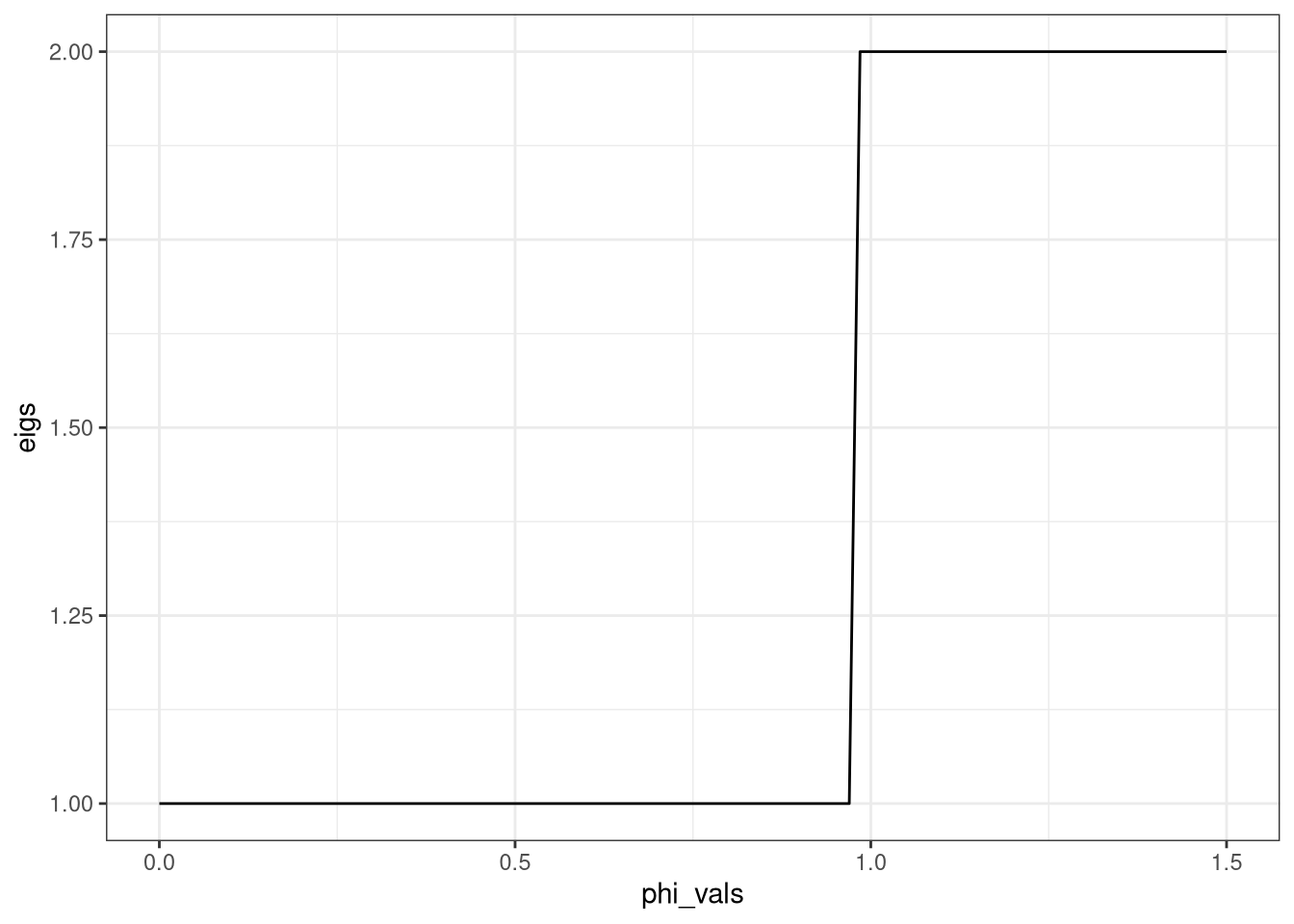Veja que o número de autovalores maiores que 1 salta um pouquinho antes de \(\phi=1\), em \(0.9848\). Isso se deve a erros numéricos e basicamente valida o principio de Taylor: para estabilizar a economia, o BC precisa aumentar a taxa de juros mais que a inflação, efetivamente aumentando a taxa de juros reais.
Uma pergunta justa é o que acontece quando o BC decide suavizar as mudanças na taxa de juros, tendo uma inércia de \(\rho\). O novo sistema se torna:
\[\begin{bmatrix} \beta & 0 & 0\\ -1 & 1 & 1\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} E_t(\pi_{t+1})\\ E_t(\tilde{y}_{t+1})\\ i_t\\ \end{bmatrix} = \begin{bmatrix} 1 & -1 & 0\\ 0 & -\sigma & 0\\ (1-\rho)\phi & 0 & \rho\\ \end{bmatrix} \begin{bmatrix} \pi_t\\ \tilde{y}_t\\ i_{t-1}\\ \end{bmatrix} + \begin{bmatrix} 0 \\ 0\\ 1\\ \end{bmatrix} \varepsilon_t\]
Vamos repetir todo o experimento:
bet = 0.99
sig = 1
rho = 0.95
phi_vals = seq(0,1.5, length.out = 100)
eigs_maior_que_um <- rep(0,length(phi_vals))
for(i in 1:length(phi_vals)){
phi = phi_vals[i]
B = rbind(c(bet,0,0),c(-1,1,1),c(0,0,1))
C = rbind(c(1,-1,0),c(0,-sig,0),c((1-rho)*phi,0,rho))
A = qr.solve(B)%*%C
eigg <- eigen(A)
eigs_maior_que_um[i] <- sum(abs(eigg$values) > 1)
}
dados_com_suav <- data.frame("phi_vals" = phi_vals,"eigs" = eigs_maior_que_um)
g <- ggplot(dados_com_suav, aes(phi_vals,eigs))
g + geom_line() + theme_bw() 
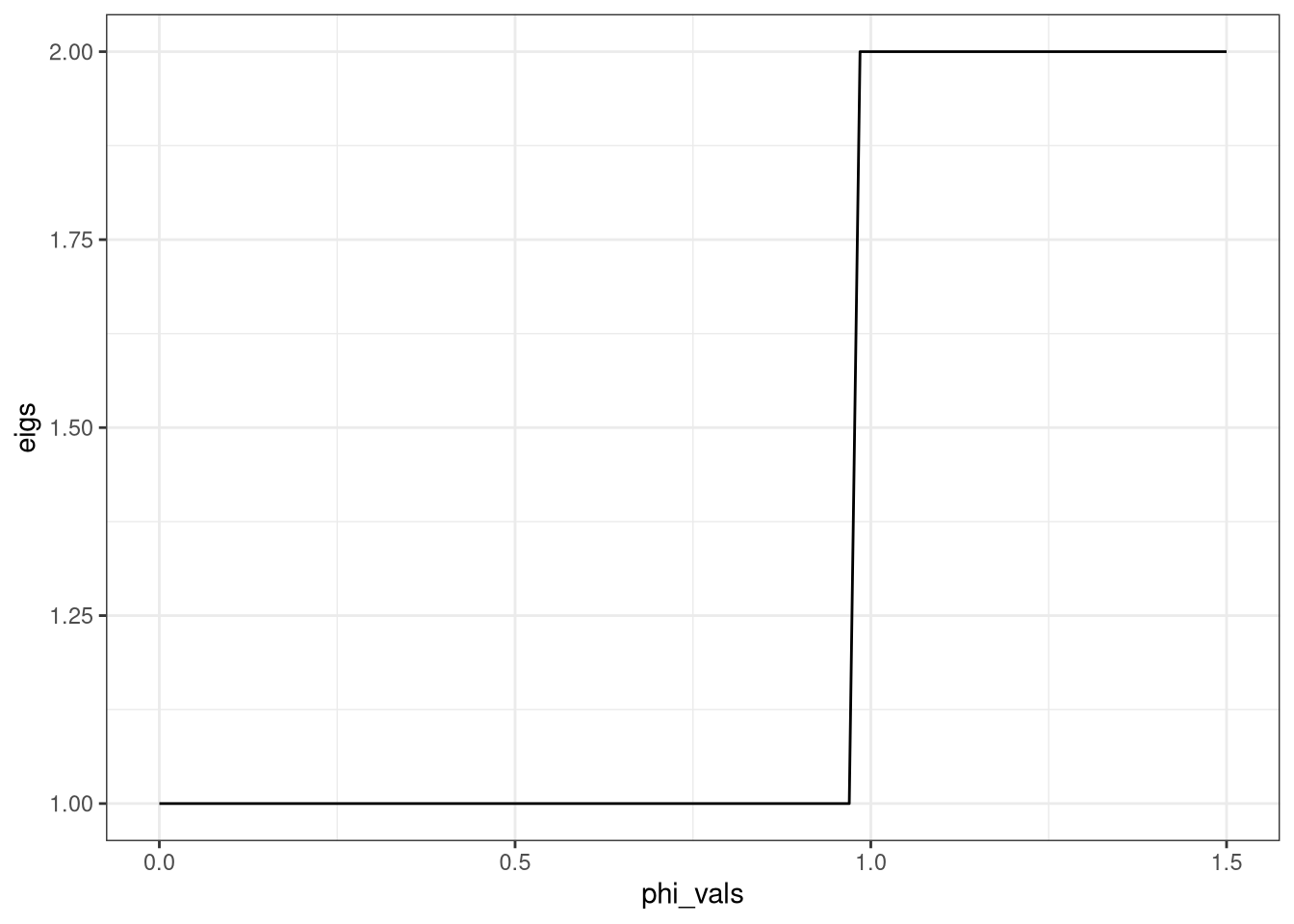
Não há nenhuma grande mudança, aparentemente.
Veja que eu fui malandro e escrevi um modelo no qual temos uma matriz \(B\):
\[B E_t(x_{t+1}) = Cx_t + \varepsilon_t\]
E portanto \(A = B^{-1}C\). Como lidar com sistemas com \(B\) singular é uma pergunta válida e não trivial de ser respondida - precisamos de usar decomposições espertas de Álgebra Linear. Mas o princípio básico de contar autovalores permance inalterado. Veja que esse método tem críticos e alternativas. Todos esses assuntos são bons temas para futuros posts do blog.
Bibliografia
Esse post se deve basicamente a aulas que eu tive e ao excelente livro do Jianjun Miao, Economic Dynamics in Discrete Time - que eu nunca canso de recomendar.