Viés de Atenuação

Esse é um desses posts curtos e simples, mas legalzinho. Surgiu de uma conversa minha com o Pedro e alguns de vocês já devem saber. É bem simples: suponha que você acha que na sua regressão x afeta y. O catch: você observa x com um erro, que é independente de x e do erro da regressão. A sua regressão vai sofrer com viés de atenuação. O parâmetro estimado vai ficar mais pŕoximo de zero, independente se ele é positivo ou negativo.

Como de praxe, começamos com uma simulação. Vou fazer uma regressão besta. A variável y vai ser $y = x +u$, mil observações. Eu vou adicionar um erro ao x - chame essa nova variável de $\tilde{x}$ e fazer uma regressão y em $\tilde{x}$.

cofs <- rep(NA,2000)

for(i in 1:2000){
  x <- rnorm(1000)
  y <- x + rnorm(1000)
  x_til <- x+ rnorm(100)
  reg <- lm(y ~ x_til)
  cofs[i] <- coef(reg)[2]
}

Vamos ver a distribuição dos coeficientes:

cofs_df <- data.frame(cofs = cofs)

ggplot(cofs_df,aes(cofs)) + geom_histogram()

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.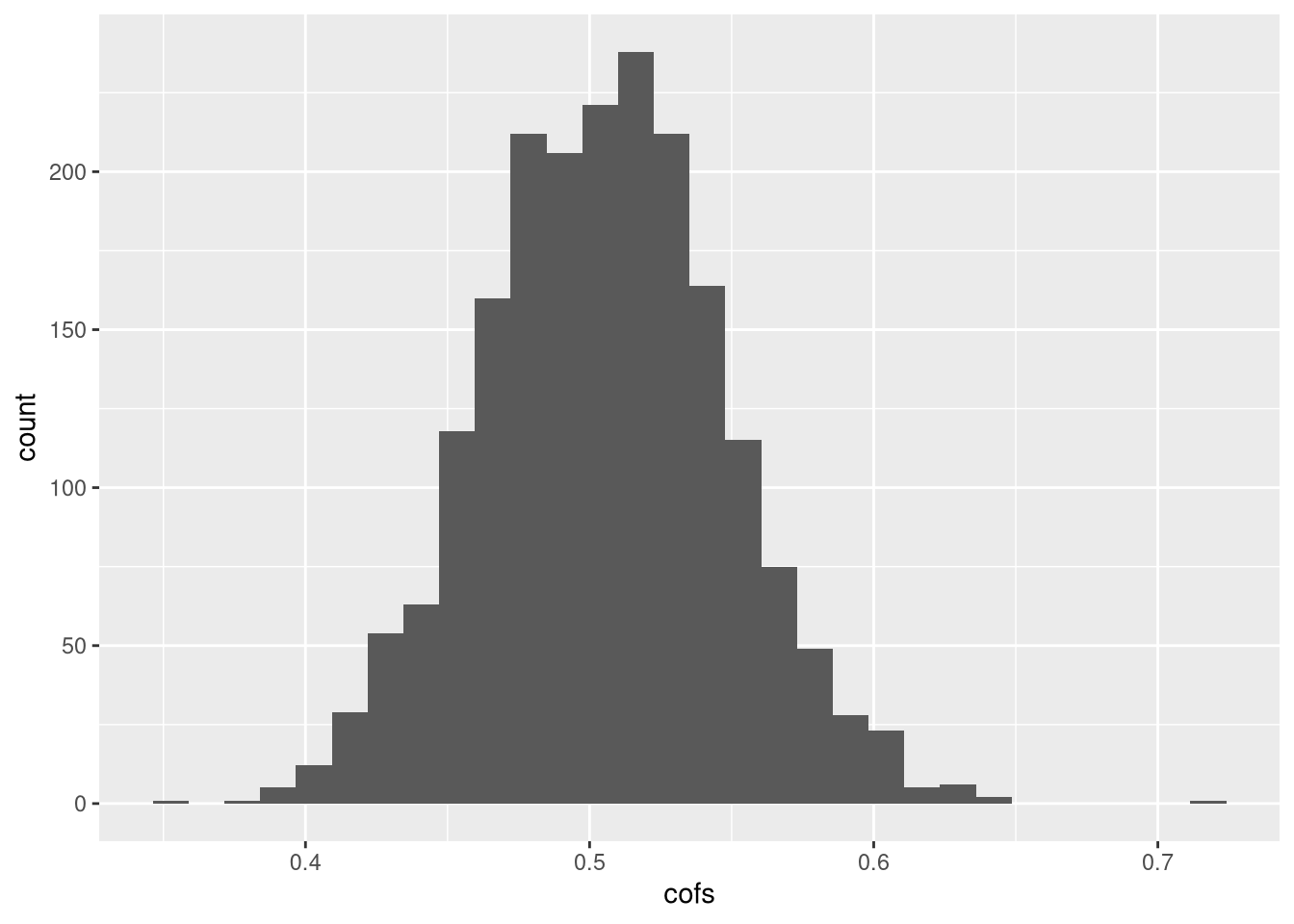

A moda está em 0.5. Por que? Bom, considere o estimador que estamos usando:

$$\hat{\beta} = \frac{\sum_{i=1}^N \tilde{x}_i y_i}{\sum_{i=1}^N \tilde{x}_i^2}$$

Note que a média de $\tilde{x}_i$ é zero. Substitua $y_i$ pelo modelo verdadeiro:

$$\hat{\beta} = \frac{\sum_{i=1}^N \tilde{x}_i (x_i + \varepsilon_i)}{\sum_{i=1}^N \tilde{x}_i^2}$$

$$\hat{\beta} = \frac{\sum_{i=1}^N (x_i + u_i) (x_i + \varepsilon_i)}{\sum_{i=1}^N \tilde{x}_i^2}$$

$$\hat{\beta} = \frac{\sum_{i=1}^N x^2_i}{\sum_{i=1}^N \tilde{x}_i^2}$$

Agora, veja que embaixo temos basicamente a variância de $\tilde{x}_i$ e em cima a variância de de $x_i$. E como $\tilde{x}_i = x_i + u_i$ portanto $Var(\tilde{x}_i) = Var(x_i) + Var(u_i) > Var(x_i)$. Então, o coeficiente está abaixo de 1. Veja que podemos trabalhar com o caso geral que ao invés de 1 temos $\beta$. Veja que como eu coloquei tudo a normal padrão, $Var(\tilde{x}_i)= 2$ e $Var(x_i) = 1$, então a conta acima dá 1/2.

Curiosamente tem uma solução super simples: variáveis instrumentais. Você pode usar qualquer variável relacionada a $x$, até outra copia com erros, desde que não seja a mesma variável. Eu vou criar uma variável nova, z, para servir como instrumento:

cofs <- rep(NA,2000)

for(i in 1:2000){
  x <- rnorm(1000)
  y <- x + rnorm(1000)
  x_til <- x + rnorm(1000)
  z <- x + rnorm(1000)
  reg <- ivreg(y ~x_til|z)
  cofs[i] <- coef(reg)[2]
}

cofs_iv_df <- data.frame(cofs = cofs)

ggplot(cofs_iv_df,aes(cofs)) + geom_histogram()

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.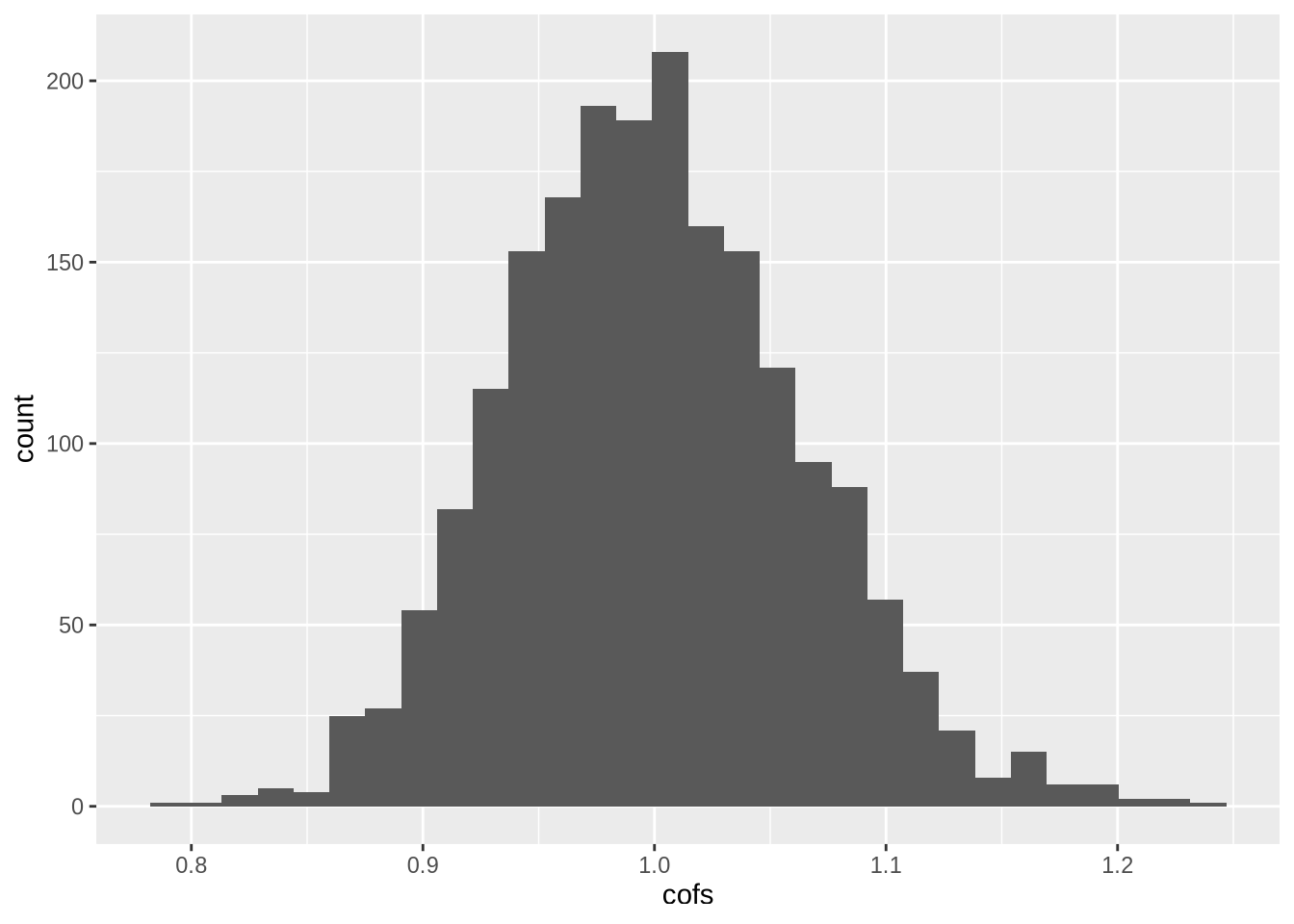

Esse é um uso bem legal de IV. Quem quiser referências: Eu imagino que quase todo livro de econometria básica deve ter isso. O Stock & Watson e Wooldridge muito provavelmente tem. O livro do Hayashi tem.