Viés de significância
Esse post trata de um troço que eu nunca tinha pensado e é sensacional, talvez dê um nó na cabeça. Ele é 100% baseado neste post aqui, que eu achei via o blog do Andrew Gelman. Você não precisa ler o post pra entender o que eu vou fazer aqui, eu vou explicar tudo.
Tem muita conta e vou deixar elas no fim. A ideia é extremamente simples: se você está numa situação em que o poder do teste é baixo e encontra um efeito significante, esse efeito provavelmente está sobreestimado.
Se você precisar refrescar a memória: o poder do teste é a probabilidade de rejeitar a hipótese nula quando ela é falsa. O nível de significância é a probabilidade de aceitar a hipótese nula quando ela é falsa, i.e. um erro de tipo I. A gente geralmente controla para o erro do tipo I e ignora o poder porque ele tende a 1, em geral.
A intuição é bem simples: se o seu teste tem poder baixo, você dificilmente vai rejeitar a hipótese nula quando ela é falsa. Isso pode acontecer especialmente se você estimar o efeito muito alto OU estimar o erro padrão muito baixo. O post foca no primeiro e vou fazer o mesmo.
Veja que isso sugere que o estimador é viesado e o viés advém todo de ficar olhando o nível de significância. Isso não seria muito grave se a gente não tivesse uma enorme paixão em publicar efeitos significantes por mais maluco que seja.
Eu vou fazer uma simulação de um caso bem simples mostrando isso: eu vou simular um amostra com média 0.1 de uma normal e testar para a hipótese nula de média 0. Eu vou colocar a variância um pouquinho alta para reduzir o poder:
library(ggplot2)
library(tibble)
library(truncnorm)
library(purrr)
rept <-3000
dados <- matrix(NA,ncol=2,nrow=rept)
for(i in 1:rept){
samp <- rnorm(100,mean=0.1,sd=1.2)
tt <- t.test(samp)
dados[i,] <- c(mean(samp), tt$p.value < 0.05)
}
df <- data.frame(dados)
df[,2] <- as.logical(df[,2])
names(df) <- c("Val","Sig")
ggplot(df,aes(Sig,Val)) + geom_boxplot() + labs(x = "P-value < 0.05?")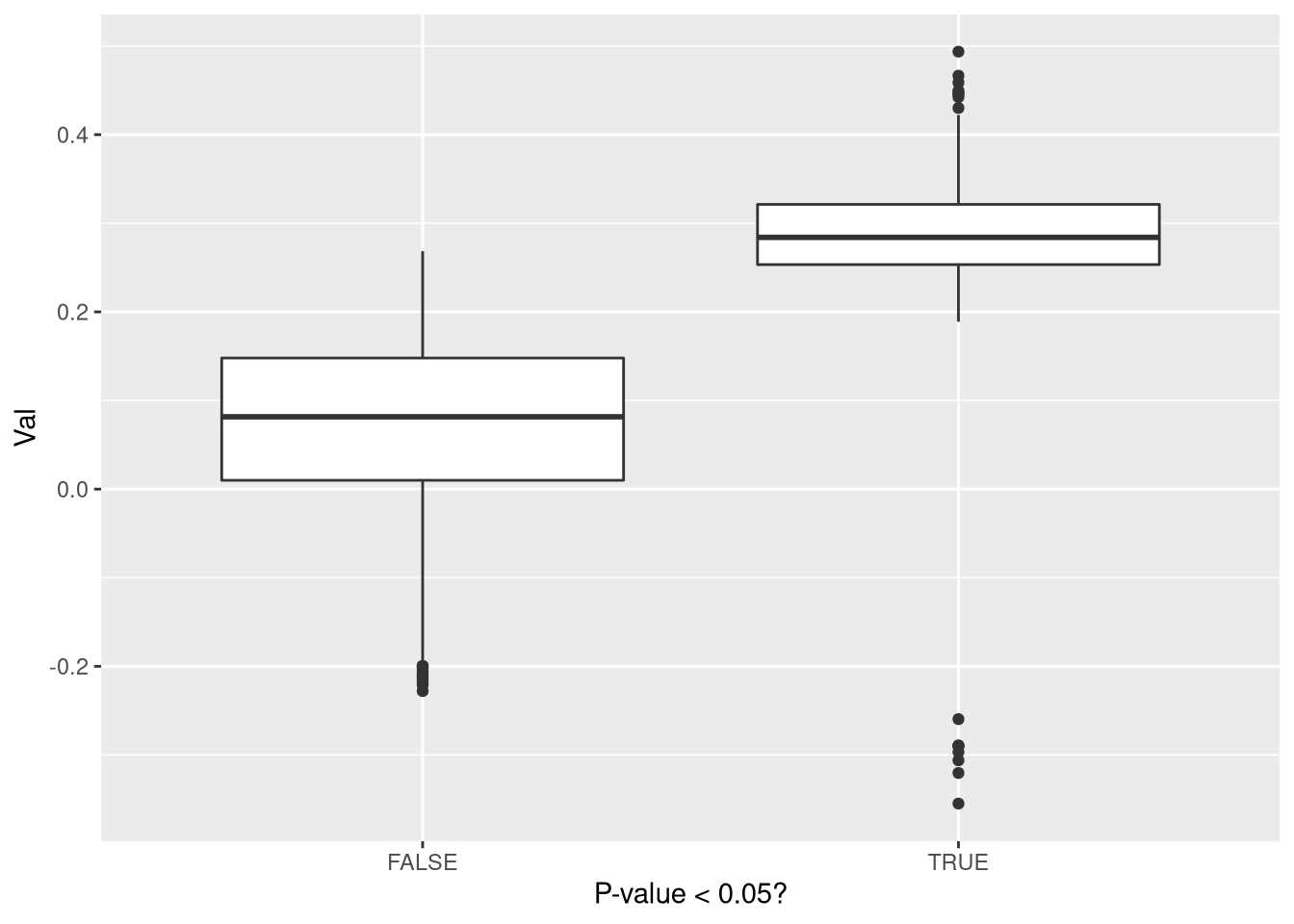
A média no caso significante é 0.2807827, enquanto a média ignorando isso é 0.0987592. Mais uma vez: isso não seria um problema muito grande se não houvesse um viés de só publicar resultado significativo ou se todos os estudos tivessem poder alto.
Vamos pra matemática por trás desse resultado
A matemática
A ideia é bem simples: em geral só se observa os coeficientes estimados quando eles ultrapassam a mágica barreira do 1.96\(\times SE\). Qual a distribuição dos coeficientes nesse caso? É uma normal truncada. A ideia guarda uma semelhança com o Tobit, onde você só observa valores acima de um certo limiar. Pra deixar as contas fáceis eu vou usar um teste unilateral de ser maior que 0 - no fim eu coloco as contas pro caso mais usual de teste bilateral, que são um pouquinho mais enjoadas. Eu vou representar a estimativa do parâmetro de interesse por \(\hat{\beta}\), o valor verdadeiro por \(\beta\), o erro padrão por SE, e o valor crítico do nível de significância \(\alpha\) por \(c_{\alpha}\). Eu vou usar \(z\) pra representar uma variável com distribuição normal padrão, que tem densidade \(\phi\) e função de distribuição acumulada \(\Phi\).
Um pequeno prólogo: lembre que o poder, que normalmente é \(1-\beta\) e vou usar \(1-b\), é a probabilidade de rejeitar H0 quando ela é falsa:
\[1-b = P\left(\frac{\hat{\beta}}{SE} > c_\alpha \bigg|\beta > 0 \right) = P\left(\underbrace{\frac{\hat{\beta} - \beta}{SE}}_{z} > c_\alpha - \frac{\beta}{SE}\right)=1-\Phi\left(c_{\alpha}-\frac{\beta}{SE}\right)\\ b = \Phi(c_\alpha - \beta/SE)\]
Do primeiro para o segundo igual eu só garanti que a variável está centrada no lugar certo para usar a normal padrão. O poder depende do nível de significância. Logo \(b\) é maior conforme \(c_\alpha\) cresce e fica claro o trade-off entre poder e erro de tipo I.
Nós queremos \(P(\hat{\beta}|\hat{\beta}/SE > c_{\alpha})\). Veja que termo que está condicionando não tem distribuição normal padrão porque faltou subtrair a média, então acertando isso nós teremos \((\hat{\beta} - \beta)/SE > c_{\alpha} - \beta/SE\). Substituindo os termos na fórmula que tá na Wikipedia nós teremos:
\[P\left(\hat{\beta}\bigg|\frac{\hat{\beta}-\beta}{SE} > c_{\alpha}-\frac{\beta}{SE}\right) = \frac{\phi\left(\frac{\hat{\beta}-\beta}{SE}\right)}{SE\left(1-\Phi\left(c_\alpha-\frac{\beta}{SE}\right)\right)}\]
Vamos focar na média, que tem na Wikipedia e dá pra mostrar usando função geratriz de momentos. A média nesse caso vai ser:
\[E(\hat{\beta}|\beta/SE > c_\alpha) = \beta + SE\frac{\phi(c_\alpha-\beta/SE)}{1-\Phi(c_\alpha - \beta/SE)}\] Veja que o denominador é o termo que encontramos para o poder e que dentro da densidade da normal temos um termo que também depende do poder:
\[E(\hat{\beta}|\beta/SE > c_\alpha) = \beta + SE\frac{\phi(\Phi^{-1}(b))}{1-b}\]
Veja que temos um viés no estimador que depende basicamente do poder do teste \((1-b)\): se \(b \rightarrow 0\), então \(\Phi^{-1}(b) \rightarrow -\infty\) e \(\lim_{x\rightarrow -\infty} \phi(x) = 0\). Trocando em miúdos, quando o poder é alto o viés é baixo. Quando o poder tende a 1, o viés desaparece.
No blog, o autor discute várias possíveis soluções e basicamente chega a conclusão que a melhor maneira é corrigir o estimador por esse viés é assumir que \(b=0\) e reduzir o estimador por \(SE \frac{\phi(c_\alpha)}{1-\Phi(c_\alpha)}2(1-F(\hat{\beta}|\beta>c_\alpha))\). Em português: você pondera o viés sob a hipótese nula do efeito ser zero vezes a probabilidade do estimador ser maior que o valor estimado na distribuição truncada. Eu vou repetir o exemplo ali de cima e no post original tem:
correction <- function(smp,alfa = 0.05){
m <- mean(smp)
se <- sd(smp)/sqrt(length(smp))
c_a <- -qnorm(alfa)
cor <- se*dnorm(c_a)/(alfa)*(1-ptruncnorm(m/se,a=c_a))
return(m-cor)
}
exper <- function(mm){
samp <- rnorm(100,mean = mm,sd = 1.2)
tt <- t.test(samp,alternative = "greater")
return(c(mean(samp),correction(samp),tt$p.value))
}
lista <- replicate(3000,0.1,simplify=F)
dff <- map(lista,exper)
dff <- do.call(rbind,dff)
dff_sig <- dff[dff[,3] < 0.05,1:2]
colMeans(dff_sig)## [1] 0.2607181 0.1587481print(paste(nrow(dff_sig), "significant cases"))## [1] "598 significant cases"tag <-c(rep("Without Correction",nrow(dff_sig)),rep("With Correction",nrow(dff_sig)))
df <- data.frame(tag = tag, vals = as.vector(dff_sig))
ggplot(df,aes(tag,vals)) + geom_boxplot()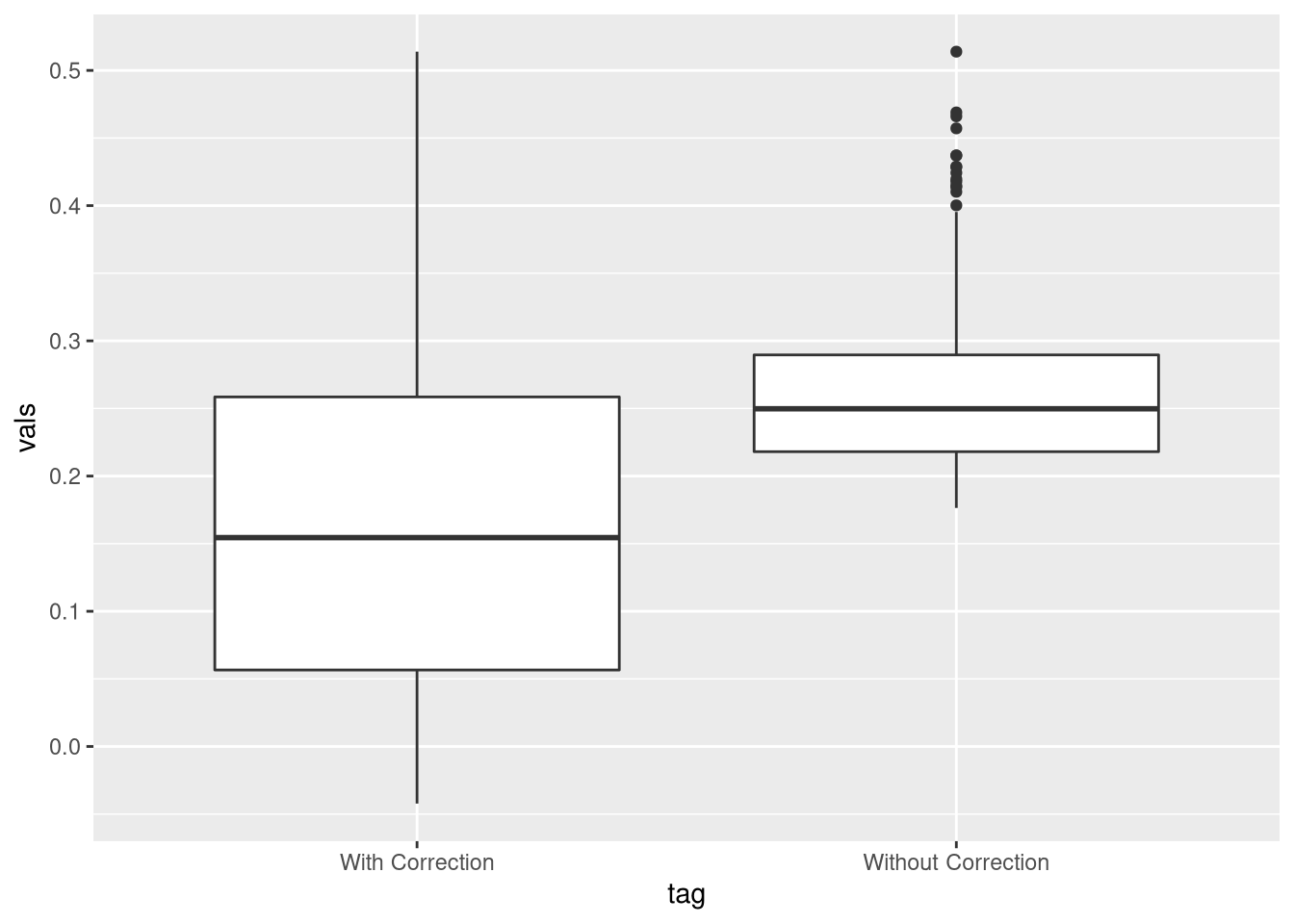
Interlúdio
Antes de discutir como implementar a mesma coisa pro caso mais usual dos economistas - regressões e testes bilaterais - eu paro para fazer a seguinte observação: isso é um maneira muito esperta de fazer encolhimento, como LASSO e o ridge fazem. Mais ainda, isso talvez sirva para justificar porque o coeficiente “encolhido” pode ser interessante para motivos além de previsão.
Uma outra solução pra isso pode ser via bootstrap. A ideia: replique a estimação várias vezes usando bootstrap e use esse coeficiente para gerar uma versão sem viés do coeficiente original. Não sei se funcionaria mas não é tão absurdo assim.
Veja que isso é um artifício de só publicar resultados significantes e só é preocupante quando o poder é baixo.
Até aqui eu só fiz o que tá no link que eu coloquei no começo do post. Vamos complicar um pouquinho.
Teste Bilateral
Agora vamos fazer o caso de teste bilateral. Aqui a coisa fica estranha: normalmente pensamos na normal truncada com observações só entre dois valores: por exemplo, \(x \sim N(0,1)\) e \(a < x < b\). Mas aqui a gente só observa se \(x>b\) ou \(x<a\), o que é esquisito. Vamos definir \(A =\{x: x> b,x<a\}\). Suponha ainda que x tem média \(\mu\) e variância \(\sigma^2\). A função de densidade é:
\[ f_x(x|x \in A) = \frac{\phi\left(\frac{x-\mu}{\sigma}\right)/\sigma} {1-\left[\Phi\left(\frac{b-\mu}{\sigma}\right) - \Phi\left(\frac{a-\mu}{\sigma}\right)\right]} \]
Depois de um bando de conta enjoada (no fim do post), é fácil encontrar:
\[E(x|x \in A) = \mu + \sigma\frac{\phi\left(\frac{a-\mu}{\sigma}\right) - \phi\left(\frac{b-\mu}{\sigma}\right)}{1-\left[\Phi\left(\frac{b-\mu}{\sigma}\right) - \Phi\left(\frac{a-\mu}{\sigma}\right)\right]}\]
A vida simplifica bastante quando \(a = c_\alpha\) e \(b = -c_\alpha\), já que \(\phi((c_\alpha-\mu)/\sigma) = \phi((-c_\alpha-\mu)/\sigma)\) e \(1-\Phi((-c_\alpha-\mu)/\sigma) = \Phi((c_\alpha-\mu)/\sigma)\). Usando os mesmos truques que lá em cima, no fim nós temos:
\[E(x|x \in A) = \mu + 2\sigma\frac{\phi\left(c_{\alpha/2}\right)}{\alpha}\]
O \(\alpha\) apareceu no denominador se deve ao fato que \(\Phi(c_\alpha)=\alpha\), por definição . Se você tá trabalhando com o nível de 5%, \(c_{\alpha/2}\) corresponde ao valor crítico para 2,5% e \(\alpha = 0.05\).
Veja que essa função densidade é bemm esquisita:
ww <- function(x,alpha,sd){
c_a <- qnorm(alpha/2)
if(x/sd < c_a){
return(pnorm(x/sd)/alpha)
} else if(x/sd < -c_a && x/sd > c_a){
return(pnorm(c_a)/alpha)
} else {
return(pnorm(c_a)/alpha + (pnorm(x/sd)-pnorm(-c_a))/alpha)
}
}
ww <- Vectorize(ww,"x")
xx <- seq(-3,3,by=0.05)
yy <- ww(xx,alpha = 0.05,sd=1)
df <- data.frame(x=xx,y=yy)
ggplot(df,aes(x,y)) + geom_line()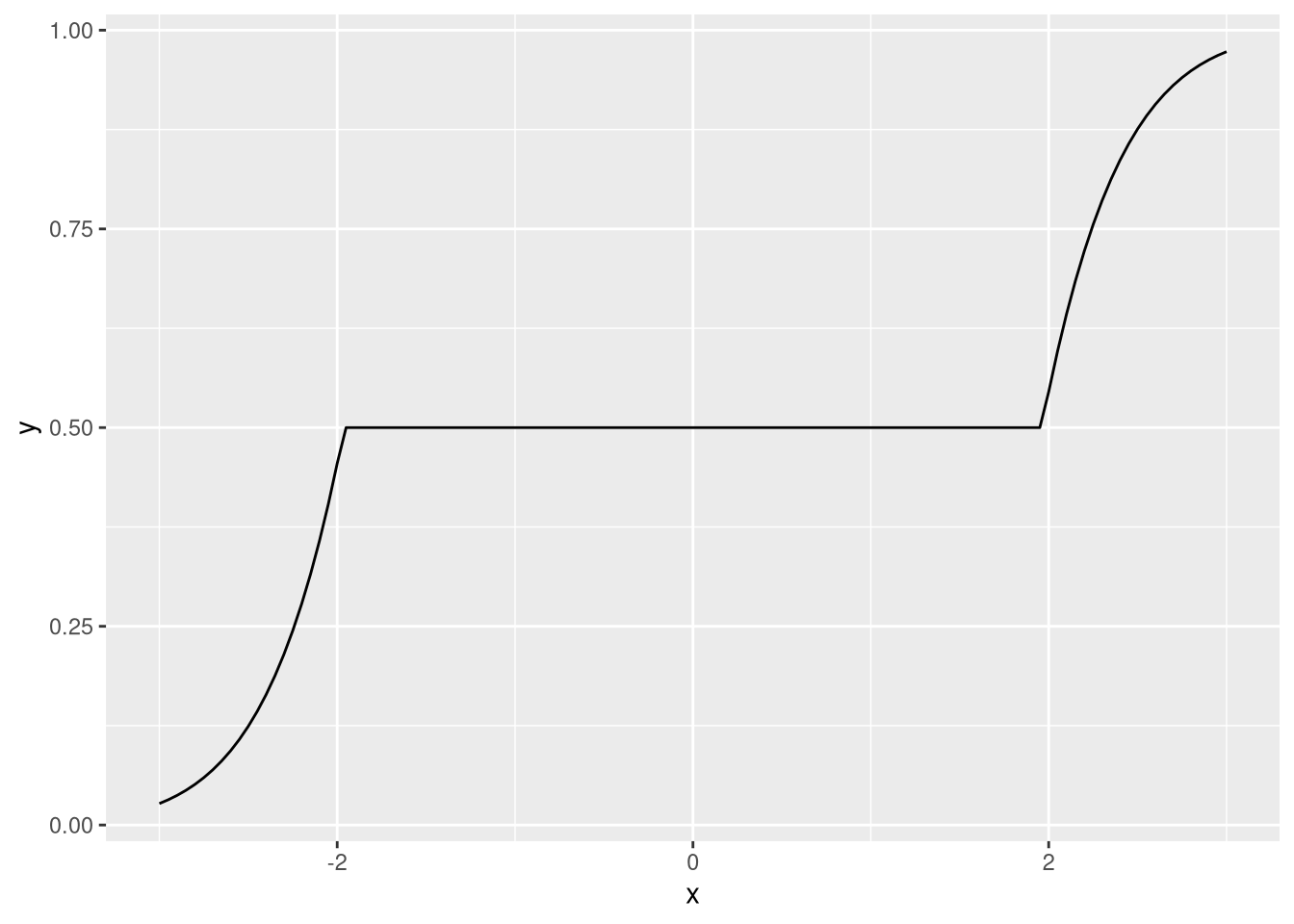
A função que faz a correção é muito parecida:
correction <- function(sample,confidence = 0.05){
m <- mean(sample)
se <- sd(sample)/sqrt(length(sample))
c_a <- qnorm(confidence/2)
cor <- se*2*dnorm(c_a)/(confidence)*2*(1-ww(abs(m),sd=se,alpha=confidence))
return(sign(m)*(abs(m)-cor))
}Ela tem uma pequena maldade pra lidar com casos negativos que é transformar tudo em valor absoluto e depois devolver o sinal (acho que o LASSO opera assim). A simulação, para valores da média entre -1 e 1:
exper <- function(m){
samp <- rnorm(100,mean = m,sd=1.5)
tt <- t.test(samp)
return(c(mean(samp),correction(samp),tt$p.value < 0.05))
}
mm <- seq(-1,1,by = 0.1)
tab <- array(NA,dim = c(2000,3,length(mm)))
for(j in 1:length(mm)){
res <- replicate(2000,mm[j],simplify = F)
res <- map(res,exper)
res <- do.call(rbind,res)
tab[,,j] <- res
}Eu salvei isso num array e vou transformar isso em um df que o ggplot aceite:
tab_sig <- list()
for(j in 1:length(mm)){
tab_temp <- tab[tab[,3,j] == T,1:2,j]
tab_sig[[j]] <- tab_temp
}
tab_all <- list()
for(j in 1:length(mm)){
tab_all[[j]] <- tab[,,j]
}
names(tab_sig) <- as.character(mm)
names(tab_all) <- as.character(mm)
mean_and_se <- function(data){
me <- colMeans(data)
se <- apply(data,2,sd)
return(c(me,se))
}
dff <- map_dfc(tab_sig,mean_and_se)
dff_all <- map_dfc(tab_all,mean_and_se)
dff <- data.frame(t(dff))
dff_all <- data.frame(t(dff_all))
dff <- rownames_to_column(dff)
dff_all <- rownames_to_column(dff_all)
names(dff) <- c("Tag","Mean","Mean_cor","SE","SE_cor")
names(dff_all) <- c("Tag","Mean","Mean_cor","SE","SE_cor")
dff[,1] <- as.numeric(dff[,1])
dff[,1] <- as.numeric(dff_all[,1])
dff_aux <- as.matrix(dff[,-1])
dff_aux <- rbind(dff_aux[,c(1,3)],dff_aux[,c(2,4)])
dff_aux_all <- as.matrix(dff_all[,-1])
dff_aux_all <- rbind(dff_aux_all[,c(1,3)],dff_aux_all[,c(2,4)])
vals <- rep(mm,2)
tags <- c(rep("Usual",length(mm)),rep("Corrected",length(mm)))
dff_aux <- data.frame(vals,tags,dff_aux)
dff_aux_all <- data.frame(vals,tags,dff_aux_all)
names(dff_aux) <- c("Vals","Tags","Mean","SE")
names(dff_aux_all) <- c("Vals","Tags","Mean","SE")Finalmente, o gráfico para os casos significantes. A linha mostra o valor verdadeiro da média:
ggplot(dff_aux,aes(Vals,Mean,ymin = Mean -2*SE,ymax = Mean+2*SE,color = Tags)) + geom_pointrange() + geom_abline()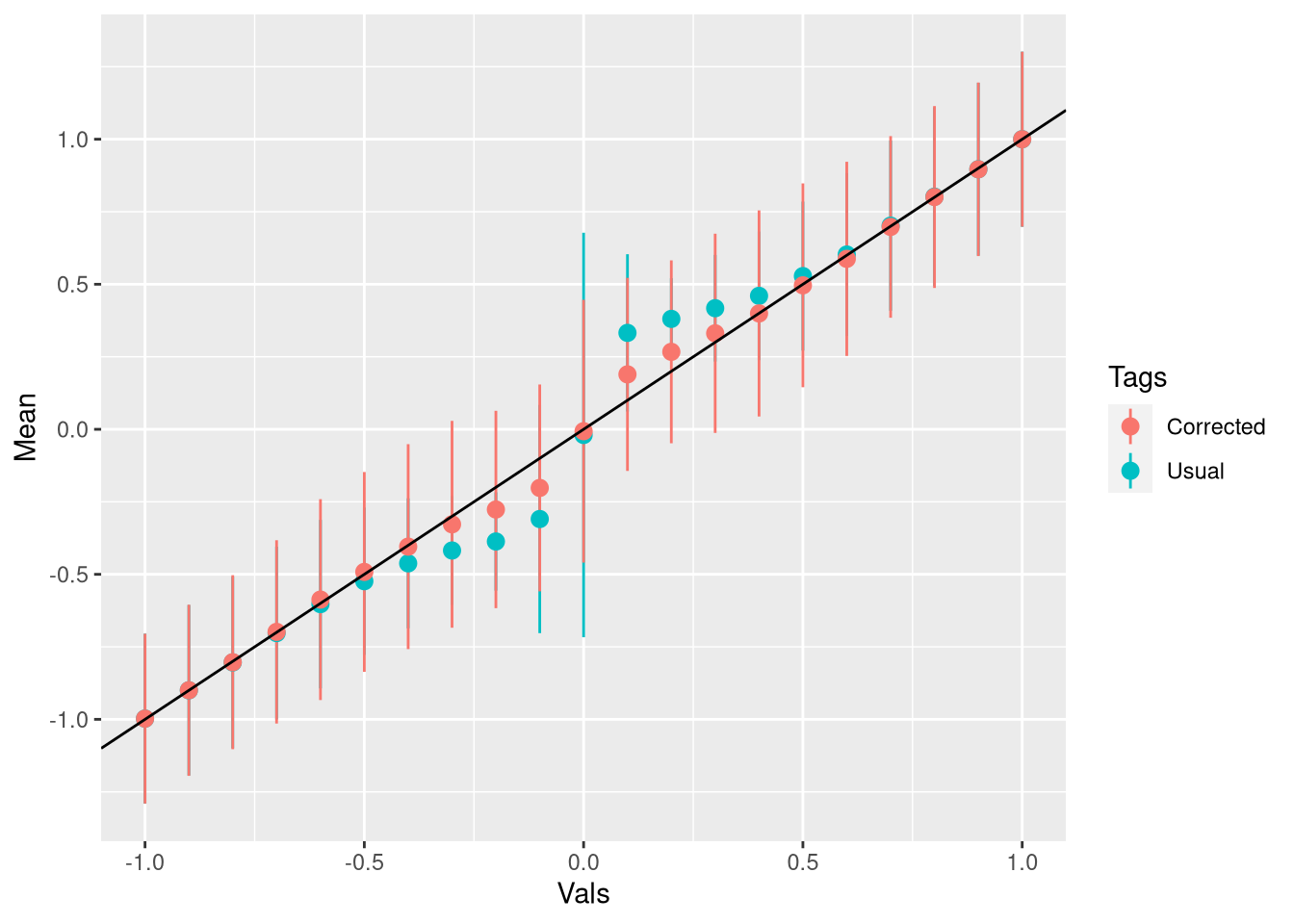
Veja que se o valor verdadeiro é grande o bastante o viés sequer existe e como a correção é ponderada pela probabilidade, ela não faz nada. Se eu pegar todas as estimativas, e não só as significantes, eu na verdade estou introduzindo viés:
ggplot(dff_aux_all,aes(Vals,Mean,ymin = Mean -2*SE,ymax = Mean+2*SE,color = Tags)) + geom_pointrange() + geom_abline()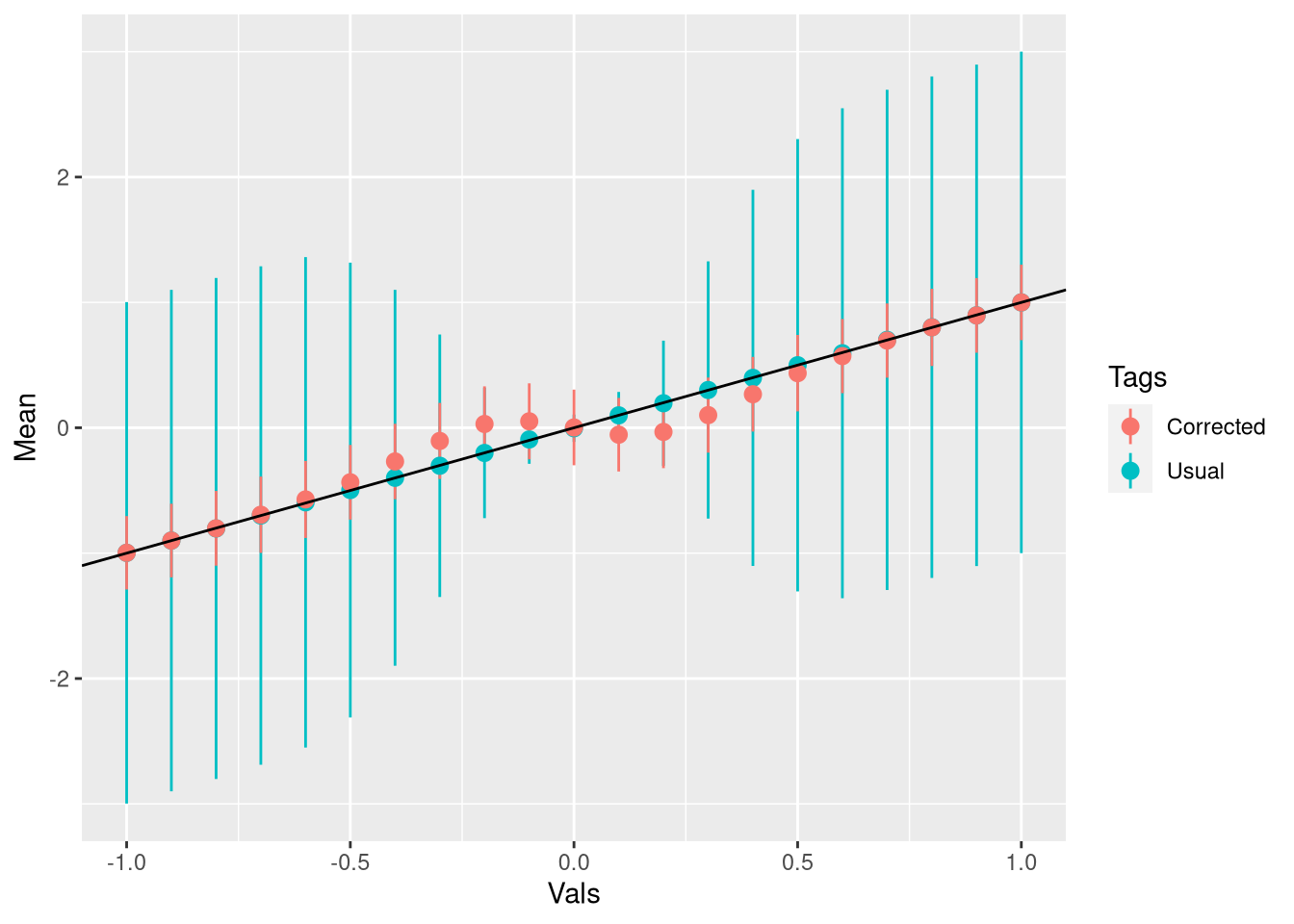
Dá pra fazer isso com coeficiente de regressão também (novamente, isso tá no post original!), e agora no lugar de \(\sigma\) você coloca o erro padrão. A função que eu escrevi pega um objeto gerado pelo lm e corrige o primeiro coeficiente que não é o intercepto - mas é fácil mudar pra ser qualquer coeficiente:
low_power_lm <- function(lm_obj,alpha = 0.05){
#n <- length(resid(lm_obj))
data <- summary(lm_obj)$coefficients[2,1:2]
b_hat <- data[1]
se <- data[2]
c_a <- qnorm(alpha/2)
cor <- se*2*dnorm(c_a)/(alpha)*2*(1-ww(abs(b_hat),alpha=alpha,sd=se))
return(sign(b_hat)*(abs(b_hat)-cor))
}Vamos fazer uma simulação e um gráfico igual fizemos pra média:
exper <- function(cof){
x <- rnorm(100)
y <- 1 + cof*x + rnorm(100)
reg <- lm(y ~ x)
summ <- summary(reg)
data <- c(summ$coefficients[2,1],low_power_lm(reg),summ$coefficients[2,4] < 0.05)
return(data)
}
mm <- seq(-1,1,by = 0.1)
tab <- array(NA,dim = c(2000,3,length(mm)))
for(j in 1:length(mm)){
res <- replicate(2000,mm[j],simplify = F)
res <- map(res,exper)
res <- do.call(rbind,res)
tab[,,j] <- res
}
tab_sig <- list()
for(j in 1:length(mm)){
tab_temp <- tab[tab[,3,j] == T,1:2,j]
tab_sig[[j]] <- tab_temp
}
tab_all <- list()
for(j in 1:length(mm)){
tab_all[[j]] <- tab[,,j]
}
names(tab_sig) <- as.character(mm)
names(tab_all) <- as.character(mm)
mean_and_se <- function(data){
me <- colMeans(data)
se <- apply(data,2,sd)
return(c(me,se))
}
dff <- map_dfc(tab_sig,mean_and_se)
dff_all <- map_dfc(tab_all,mean_and_se)
dff <- data.frame(t(dff))
dff_all <- data.frame(t(dff_all))
dff <- rownames_to_column(dff)
dff_all <- rownames_to_column(dff_all)
names(dff) <- c("Tag","Mean","Mean_cor","SE","SE_cor")
names(dff_all) <- c("Tag","Mean","Mean_cor","SE","SE_cor")
dff[,1] <- as.numeric(dff[,1])
dff[,1] <- as.numeric(dff_all[,1])
dff_aux <- as.matrix(dff[,-1])
dff_aux <- rbind(dff_aux[,c(1,3)],dff_aux[,c(2,4)])
dff_aux_all <- as.matrix(dff_all[,-1])
dff_aux_all <- rbind(dff_aux_all[,c(1,3)],dff_aux_all[,c(2,4)])
vals <- rep(mm,2)
tags <- c(rep("Usual",length(mm)),rep("Corrected",length(mm)))
dff_aux <- data.frame(vals,tags,dff_aux)
dff_aux_all <- data.frame(vals,tags,dff_aux_all)
names(dff_aux) <- c("Vals","Tags","Mean","SE")
names(dff_aux_all) <- c("Vals","Tags","Mean","SE")
ggplot(dff_aux,aes(Vals,Mean,ymin = Mean -2*SE,ymax = Mean+2*SE,color = Tags)) + geom_pointrange() + geom_abline()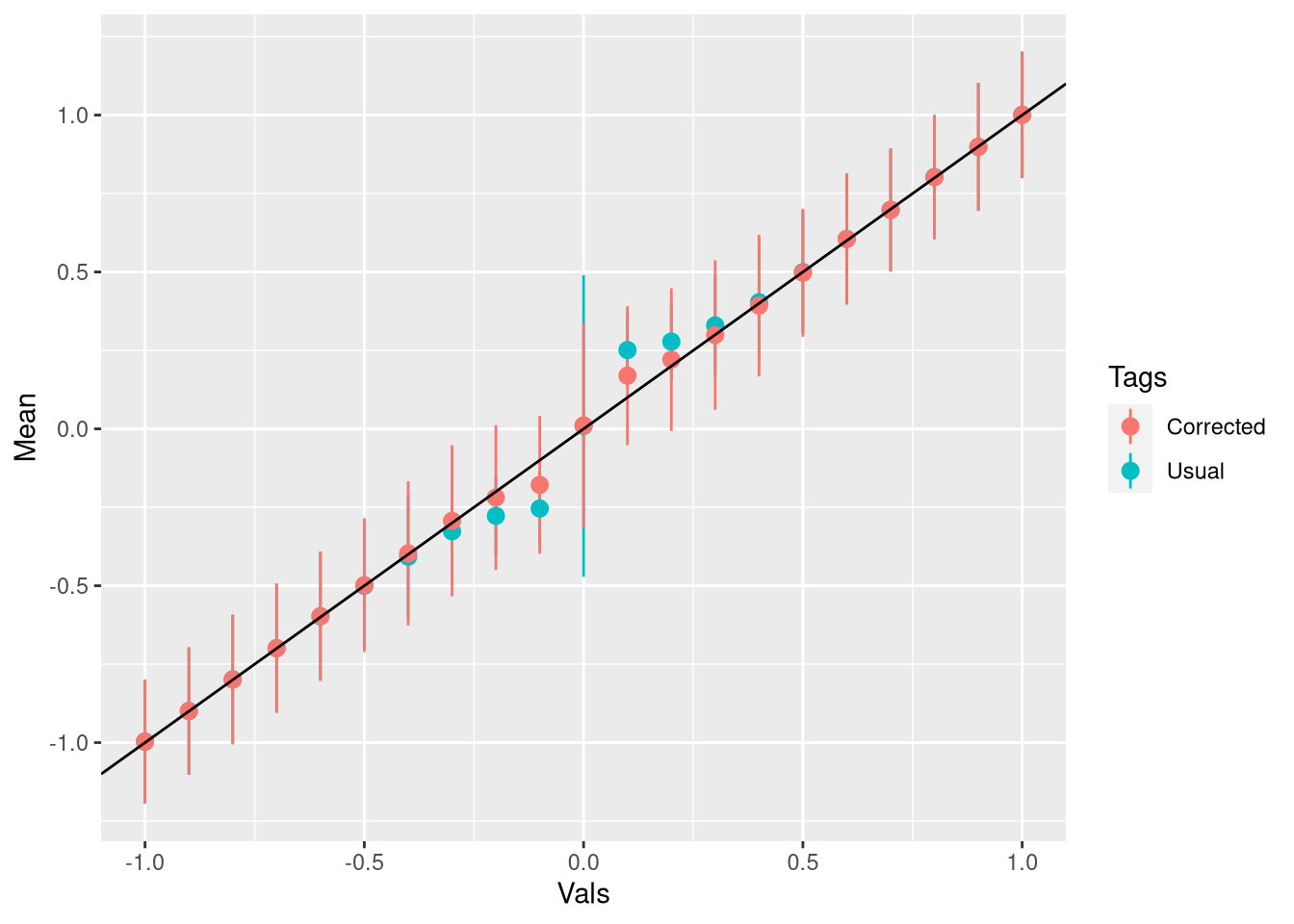
Funciona bem e não requer nenhuma simulação para resolver o problema - só uma meia dúzia de contas.
Talvez isso dê frutos e eu volte a falar disso aqui no blog - eu tenho certeza que eu não entendo isso completamente, mas eu achei tão bom que eu tinha que postar aqui.
As contas
Basicamente baseado neste pdf. Nós temos a densidade, que eu repito abaixo:
\[f_x(x|x \in A) = \frac{\phi\left(\frac{x-\mu}{\sigma}\right)/\sigma} {1-\left[\Phi\left(\frac{b-\mu}{\sigma}\right) - \Phi\left(\frac{a-\mu}{\sigma}\right)\right]}\]
Onde \(A = \{x:x>b,x<a\}\). Agora vamos fazer a conta da função geratriz de momentos e defina \(C = 1-\left[\Phi\left(\frac{b-\mu}{\sigma}\right) - \Phi\left(\frac{a-\mu}{\sigma}\right)\right]\):
\[M(t) := E(e^{tx}) = \int_A\frac{e^{xt}}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)/C dx\]
\(C\) não depende de x de maneira alguma, então a gente pode se preocupar só com:
\[\int_A \frac{e^{xt}}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)dx=\\ \int_A \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(tx-\frac{(x-\mu)^2}{2\sigma^2}\right)dx \]
Agora veja que \((x-(\mu+t\sigma^2))^2 = x^2 -2x(\mu+t\sigma^2) + (\mu+t\sigma^2)^2\). Veja que \((\mu+t\sigma^2)^2 = \mu^2 + 2t\sigma^2 \mu +t^2(\sigma^2)^2\), então:
\[\exp\left(\frac{-(x-(\mu+t\sigma^2))^2}{2\sigma^2}\right) = \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\exp(\mu{}t)\exp\left(\frac{2\mu{}t\sigma^2+t^2(\sigma^2)^2}{2\sigma^2}\right)\]
Logo:
\[\int_A \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(tx-\frac{(x-\mu)^2}{2\sigma^2}\right) = \exp\left(t\mu+t^2\sigma^2/2\right)\int_A \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{[x-(\mu+t\sigma^2)]}{2\sigma^2}\right)dx \]
Agora a integral é só a área de uma normal com variância \(\sigma^2\) e média \(\mu+t\sigma^2\). Podemos quebrar ela em duas partes correspondendo a \(A\):
\[\int_A \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-(\mu+t\sigma^2)}{2\sigma^2}\right) dx = \int_{-\infty}^a \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-(\mu+t\sigma^2)}{2\sigma^2}\right) + \int_b^{\infty} \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-(\mu+t\sigma^2)}{2\sigma^2}\right)\]
A primeira integral é \(\Phi\left(-\frac{a-(\mu+t\sigma^2)}{\sigma}\right)\) e a segunda é \(1-\Phi\left(-\frac{b-(\mu+t\sigma^2)}{\sigma}\right)\).
No fim, a função geratriz de momentos é:
\[M(t) = \exp(t\mu+t\sigma^2/2) \left(\Phi\left(-\frac{a-(\mu+t\sigma^2)}{\sigma}\right) + 1-\Phi\left(-\frac{b-(\mu+t^2\sigma^2)}{\sigma}\right)\right) \bigg/C\]
Para obter a expectância, derive a função geratriz de momentos uma vez e faça t = 0. Derivando:
\[\frac{dM(t)}{dt} = \exp(t\mu+t\sigma^2/2) \left[(\mu + \sigma^2t)\left(\Phi\left(-\frac{a-(\mu+t\sigma^2)}{\sigma}\right) + 1-\Phi\left(-\frac{b-(\mu+t^2\sigma^2)}{\sigma}\right)\right) + \sigma \left(\phi\left(-\frac{a-(\mu+t\sigma^2)}{\sigma}\right) - \phi\left(-\frac{b-(\mu+t\sigma^2)}{\sigma}\right)\right)\right] \bigg/C\]
Avalie isso em zero:
\[\frac{dM(t)}{dt} \bigg \rvert_{t=0} = \mu \underbrace{\left[\Phi\left(-\frac{a-\mu}{\sigma}\right) + 1 -\Phi\left(-\frac{b-\mu}{\sigma}\right)\right]}_{C} \bigg/C + \sigma \frac{\phi(\frac{a-\mu}{\sigma}) - \phi(\frac{b-\mu}{\sigma})}{C}\]