Remastered: Programação Dinâmica

O problema

Suponha que a gente tem um agente que vive uma vida infinita e pode escolher entre consumo e bens de capital, que são usados para produzir bens via uma função de produção \(f\). O agente tem utilidade \(u\) e existe um choque na produtividade \(\varepsilon\). Eu vou permitir que uma parte do capital passe de um período para o outro e se deprecie a taxa \(\delta\):

\[ \max_{\{c_t\}_{t=1}^{\infty},\{k_{t+1}\}_{t=1}^{\infty}} E\left[\sum_{t=1}^{\infty} \beta^t u(c_t) \right] \\ \text{sujeito a}\\ c_t + k_{t+1} = f(k_t,\varepsilon_t) + (1-\delta)k_t \]

A gente pode substituir a restrição no problema e ficar com um problema sem restrição:

\[ \max_{\{k_{t+1}\}_{t=1}^{\infty}} E\left[\sum_{t=1}^{\infty} \beta^t u(f(k_t,\varepsilon_t) + (1-\delta)k_t - k_{t+1}) \right] \\ \] Como no post anterior, eu vou escolher tudo de maneira que tenha uma solução analítica. Assim, a gente vai poder comparar a solução numérica com a solução analítica. Então:

• A utilidade vai ser \(\log(c)\)
• A função de produção vai ser \(\varepsilon_t k_t^{\alpha}\)
• A depreciação vai ser igual a 1 - nenhum capital vai passar de um período pro outro

O problema aqui é que como temos infinitos períodos, a gente tem que escolher infinitos controles. Isso é um problema, porque “derivar e igualar a zero” não vai ser suficiente para resolver o problema.

A solução é relativamente simples: como sempre tem infinitos períodos a frente, então o valor futuro não depende do ponto no tempo, ou seja, a gente pode quebrar o problema acima como:

\[ \max_{\{k_{t+1}\}_{t=1}^{\infty}} \log(\varepsilon_1k_1^{\alpha} - k_{2}) + \beta E\left[\sum_{t=2}^{\infty} \beta^{t-2} \log(\varepsilon_tk_t^{\alpha} - k_{t+1}) \right] \]

No período 2 o problema é idêntico: tem infinitos períodos a frente! Vamos chamar \(E\left[\sum_{t=2}^{\infty} \beta^{t-1} \log(\varepsilon_tk_t^{\alpha} - k_{t+1}) \right]\) de \(V_{t+1}\) e o problema se torna:

\[ V(k_{t}) = \max_{k_{t+1}} \log(\varepsilon_tk_t^{\alpha} - k_{t+1}) + \beta{}V(k_{t+1}) \quad \quad (i) \]

O problema agora é encontrar exatamente quem é a função \(V\), e a gente vai fazer a nossa coisa favorita: chutar a solução para V e iterar até convergir - a convergência é garantida pelo teorema ponto fixo de Banach, um dos xodós do blog. Veja que \(k_t\) é quanto capital foi guardado do último período. Então:

1. Postule V
2. Calcule o máximo da expressão (i) e guarde o valor do máximo
3. O novo valor do máximo é o novo chute para V
4. Itere

A gente vai precisar “guardar” a função V. A maneira que vamos usar é simples: gere um grid de pontos e calcule o máximo para cada valor de \(k_t\). Isso vai implicitamente gerar um valor futuro de \(k\), que pode muito bem não ser um ponto do grid. Então use os valores de cada ponto e interpole entre eles de alguma maneira - nós vamos usar interpolação linear, literalmente conectando ponto com o ponto seguinte por uma reta.

O código

Eu posso definir os parâmetros da função de produção e a taxa de desconto e eu vou começar por isso e carregando os pacotes:

#Os ponto e vírgula são necessários somente no blog! Senão ele vai imprimir muita coisa e atrapalhar a vizualizar

using Optim,Interpolations,Statistics,Plots

α = 0.5;
β = 0.99;
δ = 1; #full depreciation

## 1

A gente vai usar o interpolation para fazer a interpolação da função valor; o Optim vai ser encarregado de encontrar o ótimo; o Statistics vai ficar claro já já; e o Plots vai permitir a gente ilustrar os resultados. E sim, o Julia consegue lidar com parâmetros que são letras gregas!

Vamos criar as funções utilidade e de produção e as matrizes que vão salvar tanto a função valor quanto a política ótima - o valor ótimo de consumo dado o estoque de capital

iter_lim = 500;
grid_size = 100;

f(k) = k^α;
u(c) = log(c);

grid = range(0.02,5,length=grid_size);

V = zeros(iter_lim,grid_size);
V[1,:] = u.(grid);

policy = zeros(iter_lim,grid_size);

Eu estabeleci o tamanho do grid em 100. Eu poderia adicionar mais pontos ou menos, e isso afeta tanto a qualidade da solução quanto a velocidade. O iter_lim vai controlar a quantidade de iterações.

Na derivação eu usei \(V(k_t)\), ou seja, a solução depende da quantidade de capital que você leva de um período para o outro. Eu acho essa a maneira mais natural de trabalhar, mas por motivos computacionais vai ser melhor definir \(V\) como função da produção, \(y_t\). É simples passar de um para o outro usando a função de produção.

O meu chute inicial (V[1,:] = u.(grid)) involve o agente consumir toda a produção. Isso dificilmente será o ótimo, mas é um bom chute inicial: pense que se o problema fosse finito, o ótimo no último período seria consumir toda a produção (e é exatamente esse truque que justifica eu usar a função utilidade como função valor para o chute inicial).

Eu vou criar duas funções agora: uma função é a função objetivo e a outra é simplesmente uma função para facilitar a minha vida na hora de iterar:

function objective(c,y,interp)
    k_old = y^(1/α)
    next_y = f(y -c +(1-δ)*k_old)
    return -u(c) - β*mean(interp.(exp.(0.1*randn(200))*next_y))
end;

function otimo(obj,grid,interp)
    ot = optimize(x->objective(x,grid,interp),0.01,grid-0.0001)
    return ot.minimum,ot.minimizer
end;

A função objetivo recebe o ponto que a gente está hoje, \(y\) (quanta produção é possível dado o capital herdado do último período); um objeto que faz a interpolação, \(interp\); e o consumo, \(c\), que é a variável de escolha. A segunda função simplesmente recebe a função objetivo, o ponto do grid que a gente tá e a função que faz a interpolação e realiza a otimização. Como o otimizador só faz minimização, multiplicar por \(-1\) transforma o máximo em mínimo. Como a otimização é univariada, o algoritmo precisa do intervalo para buscar os valores: eu to estabelecendo o consumo como no mínimo um número pequeno - pequeno demais vai gerar algum número próximo de \(-\infty\). O valor máximo não pode ser consumir tudo porque isso implica em produção zero no próximo período e isso também gera um \(-\infty\).

Eu escrevi muita infraestrutura antes de começar a iteração de fato. A vantagem disso é que eu posso checar que todas as funções funcionam antes de rodar o loop e o loop fica extremamente conciso, especialmente usando o map:

global j = 2;
global err = 1;

@time while j <= iter_lim && err > 1e-5
    interp = LinearInterpolation(grid,V[j-1,:])
    res = map(y->otimo(objective,y,interp),grid)
    V[j,:] = map(i->-1*res[i][1],1:grid_size)
    policy[j,:] = map(i->res[i][2],1:grid_size)

    global err = maximum(abs.(V[j,:] - V[j-1,:]))

    global j += 1

    mod(j,50) == 0 ? println("Interation ",j," error ",err) : nothing

end

## Interation 50 error 0.8768164087817638
## Interation 100 error 0.5655717548204677
## Interation 150 error 0.3367009294676109
## Interation 200 error 0.23243552432830938
## Interation 250 error 0.15783334358057743
## Interation 300 error 0.09153294330783979
## Interation 350 error 0.07163775730728617
## Interation 400 error 0.059016687308826477
## Interation 450 error 0.062496249791820446
## Interation 500 error 0.052774645535947684
##  27.932710 seconds (93.45 M allocations: 14.099 GiB, 11.74% gc time, 17.97% compilation time)

Primeiro: você precisa definir j e err como global para eles serem acessados pelo loop corretamente - senão ele vai criar variáveis com esse nome dentro do escopo do loop. Mais importante, você precisa acessar elas dentro do loop usando a keyword global. O while permite que o código pare de rodar se uma das duas coisas acontecer: ou atingir o máximo de iterações, que eu defini lá em cima ou se a diferença entre a função valor de duas iterações diferentes for menor que 1e-5.

O primeiro map aplica a função otimo para cada ponto do grid. Eu usei uma função anônima (y->otimo(objective,y,interp)) para o código passar o valor de cada ponto do grid para a função que eu fiz para buscar o ótimo. Os dois maps seguintes só pegam o resultado do primeiro map e quebra ele - o Julia permite arrays em que cada elemento tem mais de uma entrada, então formalmente o objeto res tem 100 entradas, e cada entrada é um vetor. Eu podia ter feito isso com um for:

while j <= iter_lim && err > 1e-5
    interp = LinearInterpolation(grid,V[j-1,:])
    for i = 1:grid_size
        ot = optimize(c->objective(c,grid[i],interp),0.01,grid[i] - 0.0001)
        V[j,i] = -ot.minimum
        policy[j,i] = ot.minimizer
    end

    global err = maximum(abs.(V[j,:] - V[j-1,:]))

    global j += 1

     mod(j,50) == 0 ? println("Interation ",j," error ",err) : nothing

end

Note que em ambos os casos eu tenho que trocar o sinal de \(V\), porque a gente usou \(-V\) na minimização e queremos \(V\) e não \(-V\) - esse é um erro fácil de cometer, e que portanto eu cometi e a iteração não fazia nenhum sentido. Em uma outra observação, a linha mod(j,50) == 0 ? println("Interation ",j," error ",err) : nothing é uma maneira extremamente concisa de escrever:

if(mod(j,50) == 0)
  println("Interation ",j," error ",err)
end

O nothing indica que caso a condição não seja verdade, nada deve ser feito.

Tem uma pequena diferença entre a versão usando map e a versão usando for: a versão usando map é um pouco mais rápida. Fora do RStudio, a versão com map roda em 21s e a com for demora 25s. A diferença é muito pequena e provavelmente se deve menos ao for e mais ao fato de como a linguagem funciona (funções são sempre mais rápidas devido a compilação, por exemplo).

Dito isso, vamos ver como fica a função consumo e comparar ela com a função consumo obtida analiticamente:

plot(grid,policy[iter_lim,:], lab = "Numerical Solution", legend = :topleft);
apol(grid) = (1-α*β)*grid;
plot!(grid,apol.(grid), lab = "Analytical Solution");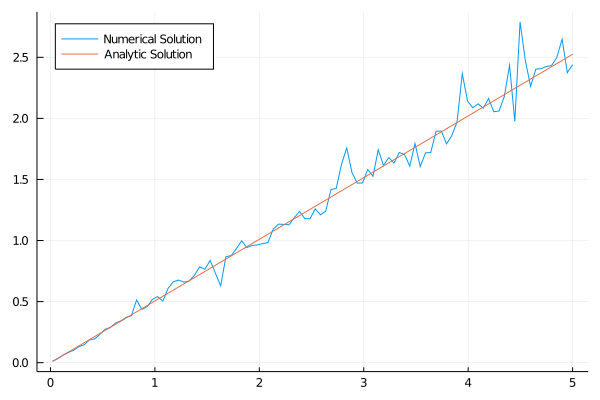

Eu não fiquei inteiramente satisfeito com o quão bagunçado tava a linha no fim e eu aumentei o número de iterações para mil, com os seguintes resultados:

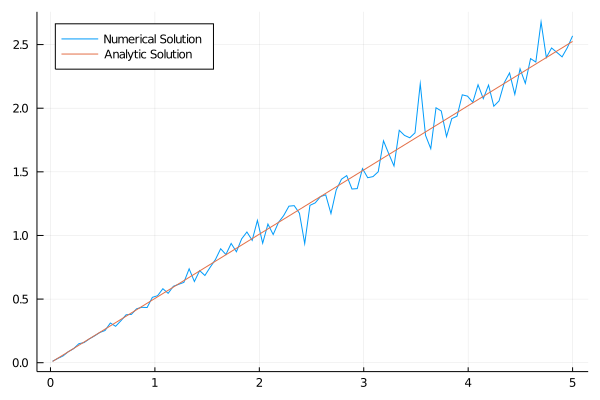
Dá pra melhorar? Eu to usando só 100 pontos para calcular a expectância, de repente 400 pontos fazem um trabalho melhor (mantendo mil iterações):

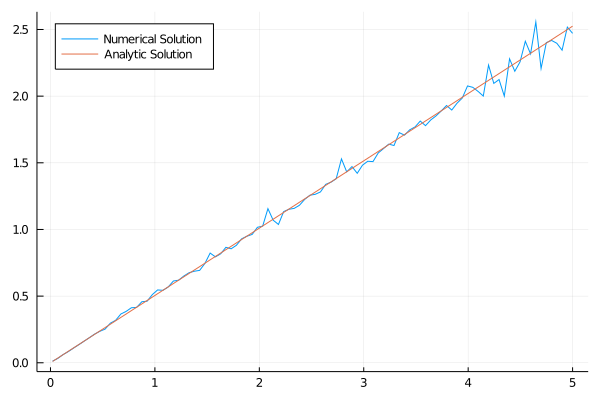
Melhorou! Mas eu realmente gostaria de ver menos ruído. Aumentar o número de iterações e o número de pontos para calcular a expectância provavelmente resolvem isso. Métodos usando as condições de primeira ordem, que eu já discuti aqui, tendem a convergir mais rápido, então menos iterações vão ser necessárias.