Concentração de Medida

Este é um post meio maluco, porque é absolutamente específico a coisas de machine learning e não é nem de perto uma aplicação prática. Mas é um tópico que é muito interessante e que eu acho que é bastante acessível.

Vamos começar com um velho conhecido, a desigualdade de Chebyschev:

\[P(|X-\mu| > t) \leq \frac{Var(x)}{t^2}\]

Nós todos conhecemos essa desigualdade, que é usada como uma maneira de “provar” que a média amostral é um estimador consistente: a variância da média de um processo i.i.d. com variância \(\sigma^2\) é \(\sigma^2/n\) e portanto Chebyschev nos dá:

\[P(|\bar{X}-\mu| > t) \leq \frac{\sigma^2}{nt^2}\]

Então quando \(n \rightarrow \infty\), \(\bar{X}\) está próximo de \(\mu\). A Desigualdade de Chebyschev é uma aplicação de um resultado mais elementar, a desigualdade de Markov, que diz que para qualquer variável aleatória positiva:

\[P(X > t) \leq \frac{E(X)}{t}\]

Se você trabalhar com \((X-\mu)^2\) e \(t^2\), você chega na desigualdade de Chebyschev.

Existem outras maneiras de deixar uma variável positiva, e uma bacana é usando \(e^X\). Eu vou assumir média zero e trabalhar com \(e^{\lambda{}t}\) e \(e^{\lambda{}x}\):

\[P(X > t) = P(e^{\lambda{}X} > e^{\lambda{}t}) \leq \frac{E(e^{\lambda{}X})}{e^{\lambda{}t}}\]

Agora, alguns de vocês sabem, mas apenas para garantir: \(E(e^{\lambda{}X})\) é conhecido como a função geratriz de momentos. Nem todas as distribuições tem função geratriz de momentos. A parte bacana é que as derivadas com respeito a \(\lambda\) da função geratriz de momentos (avaliada em \(\lambda=0\)) nos dão os momentos da distribuição. Por exemplo, a normal com média \(\mu\) e variância \(\sigma^2\) tem como função geratriz de momentos \(e^{\lambda\mu + \lambda^2 \sigma^2/2}\). Tire as derivadas e avalie em \(\lambda=0\) para se convencer de que o que eu disse é verdade.

Sabendo disso, nós podemos dizer que se \(X\) é Normal com média zero e variância \(\sigma^2\), então a desigualdade que eu coloquei com exponencial implica:

\[P(X > t) \leq e^{\lambda^2\sigma^2/2 - \lambda{}t}\]

Isso é verdade para qualquer \(\lambda\). A gente pode escolher o \(\lambda\) que minimiza o valor na desigualdade, via as condições de primeira ordem, que nos dão:

\[\lambda\sigma^2 - t = 0 \therefore \lambda = \frac{t}{\sigma^2}\]

Onde eu usei que \(\log\) é monotônico e portanto não altera o ponto do máximo. Devolvendo isso para a desigualdade nós temos:

\[P(X > t) \leq \exp\left(\frac{t^2\sigma^2}{2(\sigma^2)^2} - \frac{t^2}{\sigma^2}\right) = e^{-t^2/(2\sigma^2)}\] Essa desigualdade também tem um nome: Desigualdade de Chernoff (pra ser honesto: tudo que eu li disso é em inglês. Em inglês chamam de Chernoff Bound, mas eu traduzi para desigualdade já que temos a desigualdade de Chebyschev)

Deixa eu convencer vocês que isso é bem legal: eu vou simular 10 mil sorteios da normal padrão e comparar o que cada uma dessas desigualdades significa. Eu vou contar a probabilidade de ser maior que \(t\) simplesmente computando a frequência em que os valores simulados são maiores que \(t\) para um grid de valores \(t\). Eu também vou trabalhar com o valor absoluto de \(X\):

library(ggplot2) #gráficos bonitos
library(purrr) #pra computar o valor em cada um dos pontos do grid sem usar um for
library(tidyr) #pros dados ficarem do formato certo pro ggplot

n <-10000 #tamanho da amostra
grid_size <- 50 #tamanho do grid

tt <- as.list(seq(0.1,2,length.out = grid_size)) #o grid

yy <- rnorm(n)

freq <- map_dbl(tt,~(sum(abs(yy) > .))/n)

tt <- do.call(c,tt)

df <- data.frame("grid" = tt,"Empiric" = freq,"Chernoff" = 2*exp(-tt^2/2),"Chebyschev" = 1/tt^2)

df2 <- pivot_longer(df,cols = c("Empiric","Chernoff","Chebyschev"))

ggplot(df2,aes(grid,value,color = name)) + geom_line()

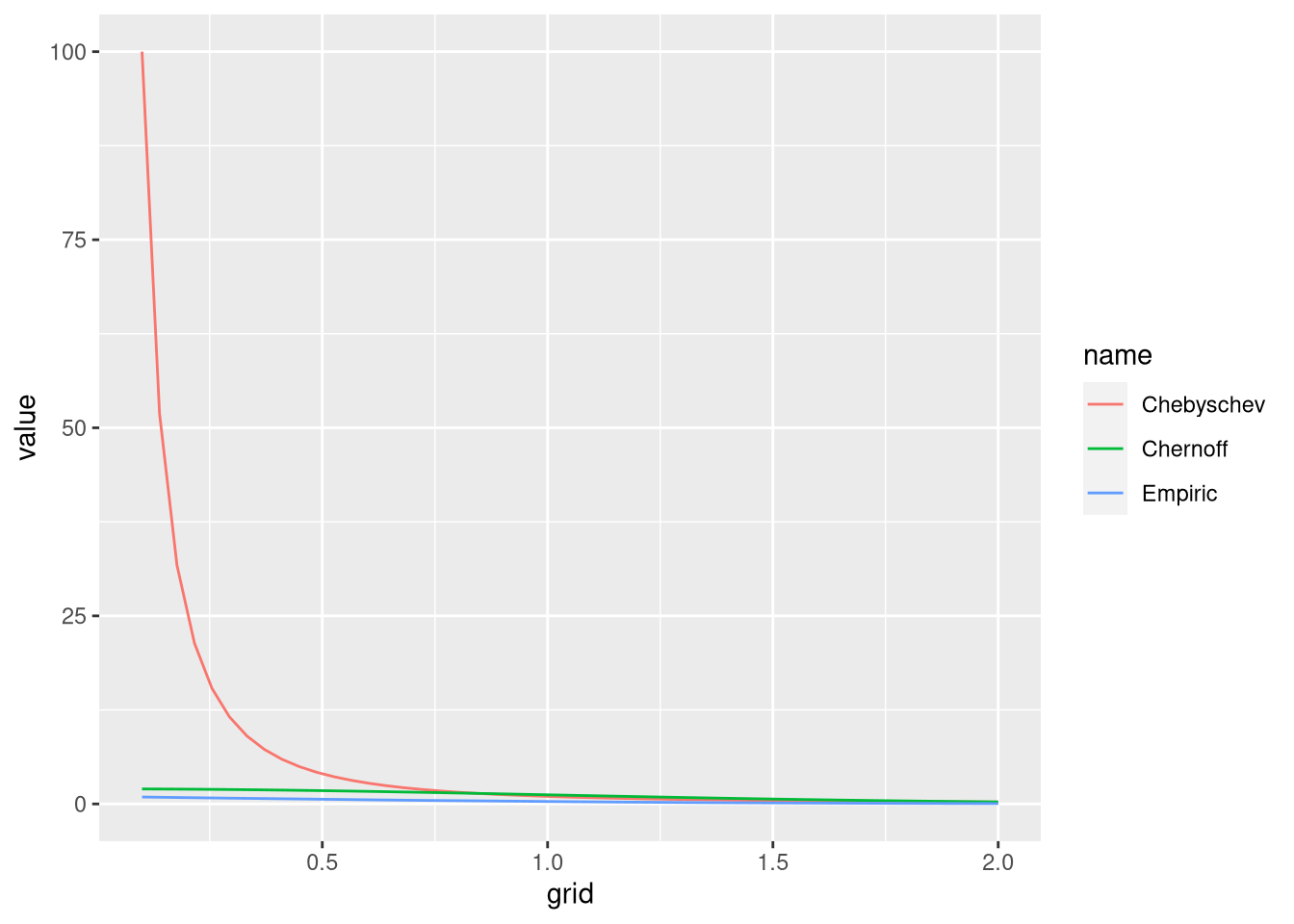
Veja que eu fiz um hardcode de que a variância é 1. Fica bem claro que:

1. As duas desigualdades fazem o que prometem: elas estão sempre acima na probabilidade verdadeira

2. Chebyschev distorce totalmente o gráfico porque é extremamente generosa

Vamos eliminar Chebyschev do gráfico:

df3 <-df[,-4]

df3 <- pivot_longer(df3,cols = c("Empiric","Chernoff"))

ggplot(df3,aes(grid,value,color = name)) + geom_line()

Veja que essa cota é bem generosa, mas bem melhor que a desigualdade de Chebyschev. Obviamente, pagamos um preço por isso: nem todas as funções com variância finita tem função geratriz de momentos.

Um fato mais interessante é que você pode usar a desigualdade de Chernoff, exatamente como posta acima, para outras distribuições além da gaussiana. Basicamente, você está exigindo que a cauda da distribuição caia tão rápido quanto a gaussiana. Distribuições que atendem a esse requisito são chamadas de subgaussianas. Todas as distribuições com suporte finito atendem a esse pré requisito, por exemplo. Por sinal, \(\sigma\) no caso mais geral não precisa ser a variância da distribuição. Nem todas as distribuições são subgaussianas: a qui-quadrado não é sub gaussiana, e é uma distribuição extremamente comum em estatística.

Veja que essa cota depende exponencialmente de \(t^2\), ao contrário de Chebyschev que depende de \(1/t^2\). Isso é um ganho dramático: com altíssima probabilidade a massa da distribuição está concentrada. Além de ser bem bacana, isto aparece em várias situações em machine learning. Mas eu não consegui criar nenhum exemplo simples em que isso fique evidente, então fica pro próximo post.