Estimador James-Stein e admissibilidade
Antes do post: eu (e o Pedro, pelo jeito) andei sem tempo. O último post foi em junho. Julho, agosto e setembro foram enrolados, mas por um bom motivo. Com um pouco de sorte eu serei capaz de fazer posts com mais regularidade no resto do ano
Eu já escrevi posts no blog sobre o LASSO, um método de estimação de modelos lineares que induz esparsidade. A motivação daquele post - e do meu interesse inicial no LASSO - era que o LASSO é uma maneira de selecionar variáveis automaticamente.
Existe uma outra motivação para métodos de encolhimento, que data da década de 60. Ela depende de teoria da decisão, mas é extremamente razoável e explicável. Eu vou discutir a ideia e mostrar o estimador que foi criado a partir que surgiu da discussão, chamado de estimador James-Stein.
Teoria da decisão, admissibilidade
Se você já fez um curso de estatística, uma das perguntas é como analisar um estimador qualquer. Existem várias maneiras de avaliar estimadores: nós podemos querer considerar só estimadores não viesados, e dentre eles os com menor variância; nós podemos querer apenas os estimador não viesados e lineares. etc. Um critério muito comum para avaliar o estimador \(\hat{\theta}\) é o erro quadrático médio (EQM): \(E[(\hat{\theta} - \theta_0)^2]\), no qual \(\theta_0\) é o valor verdadeiro do parâmetro. Nós precisamos usar o valor esperdo porque \(\hat{\theta}\) é uma variável aleatória que depende dos dados. Eu vou representar o EQM por \(\mathcal{R}(\theta,\hat{\theta})\).
Veja que o erro quadrático médio pode ser decomposto em duas partes, uma sendo a variância do estimador e outra que é o viés:
\[ E[(\hat{\theta} - \theta_0)^2] = (E[\hat{\theta}] - \theta_0)^2 + Var(\hat{\theta}) \]
Veja que o EQM depende do valor verdadeiro do parâmetro. Em geral, nós poderíamos esperar que se temos dois estimadores, \(\hat{\theta}_1\) e \(\hat{\theta}_2\) e dois valores do parâmetro, \(\theta_1\) e \(\theta_2\), então pode acontecer de \(\mathcal{R}(\theta_1,\hat{\theta}_1) < \mathcal{R}(\theta_1,\hat{\theta}_2)\) e \(\mathcal{R}(\theta_2,\hat{\theta}_2) < \mathcal{R}(\theta_2,\hat{\theta}_1)\).
Se existirem dois estimadores \(\hat{\theta}\) e \(\tilde{\theta}\) e para todos os valores possíveis do parâmetro \(\theta\) nós temos \(\mathcal{R}(\theta,\hat{\theta}) \leq \mathcal{R}(\theta,\tilde{\theta})\) e para pelo menos um valor do parâmetro1 a desigualdade for estrita, então alguém pode argumentar que nós não deveríamos considerar o estimador \(\tilde{\theta}\): em qualquer situação, existe um estimador que nunca é pior do que ele. Nesse caso, nós dizemos que o estimador \(\tilde{\theta}\) é inadmissível.
Se nós estamos trabalhando apenas com o estimadores não viesados, então minimizar o erro quadrático médio é equivalente a buscar o estimador com menor variância. Por exemplo, para o modelo linear, o estimador de mínimos quadrados é o melhor estimador linear não viesado.
Estimador James-Stein
O parágrafo anterior deixa em aberto se existe um estimador, possivelmente não linear e possivelmente viesado, que tenha EQM menor que o estimador de mínimos quadrados. Veja que, pela decomposição do EQM em viés e variância, é possível imaginar que introduzir um pouquinho de viés reduza o EQM se esse viés reduzir muito a variância.
Foi exatamente este tipo de consideração que fez o Stein procurar um estimador que fizesse o estimador de MQO ser inadmissível: é o estimador James-Stein, os nomes dos autores do paper que introduz o estimador. O estimador James-Stein para o modelo linear é uma função do estimador de mínimos quadrados. Eu vou representar o estimador James-Stein por \(\hat{\beta}_{JS}\) e o de mínimos quadrados por \(\hat{\beta}_{MQO}\)
\[ \hat{\beta}_{JS} = \hat{\beta}_{MQO} - \frac{c\sigma^2}{\hat{\beta}_{MQO}^T X^{T} X \hat{\beta}_{MQO}} \hat{\beta}_{MQO} \]
O superescrito \(T\) é a transposta da matriz. O termo \(\hat{\beta}^T X^T X \hat{\beta}\) é um escalar. Os parâmetros acima que não foram discutidos anteriormente são \(\sigma^2\), que é a variância do erro, e \(c\), que é uma constante. Para o modelo linear com erros com distribuição normal, o estimador James-Stein minimiza o EQM quando \(c = p-2\) e \(p\) é o número de variáveis (e nós só podemos considerar modelos com \(p > 2\), ou seja, mais de duas variáveis).
Simulando
O paper obteve os resultados analíticos, mas eu vou fazer simulações para mostrar que o estimador James Stein realmente tem um EQM menor que o estimador de MQO. Eu vou querer mostrar duas coisas:
O estimador James-Stein realmente garante que o estimador de OLS é inadmissível
Se os erros são normais, \(p-2\) é o valor ótimo para \(c\).
Eu vou implementar três funções que vão fazer as simulações necessárias. Todos os parâmetros do modelo vão ter o mesmo valor em cada simulação - exceto o intercepto, que é sempre zero.
A primeira função pega um valor pro parâmetro verdadeiro, um conjunto de valores para o parâmetro \(c\) (que eu chamei, talvez confusamente, de regs, para regularização), o tamanho da amostra \(n\) e a quantidade de variáveis (além do intercepto) \(k\):
simul_various_regs <- function(true_par,regs,n,k){
x <- matrix(rnorm(n*k),ncol = k)
y <- x%*%rep(true_par,k) + rnorm(n)
res <- lm(y ~ x)
ols <- coef(res)
shrink_js <- n*as.vector(t(ols[-1])%*%cov(x)%*%ols[-1])
ols_mat <- t(replicate(length(regs),ols[-1]))
stein <- ols_mat - as.matrix(regs)%*%ols[-1]/shrink_js
stein <- cbind(ols[1],stein)
rownames(stein) <- regs
return(rbind(ols,stein))
}A função retorna os valores do estimador de mínimos quadrados (OLS) e as várias versões do estimador James-Stein. Eu implementei o estimador James-Stein como uma multiplicação de matriz, e pro benefício do leitor eu vou colocar a conta com as matrizes pro caso de duas variáveis (todos os \(\hat{\beta}\) são estimadores de mínimos quadrados) e dois possíveis valores para \(c\), \(c_1\) e \(c_2\):
\[ \begin{bmatrix} \hat{\beta}_1 & \hat{\beta}_2\\ \hat{\beta}_1 & \hat{\beta}_2\\ \end{bmatrix} - \frac{1}{\hat{\beta}^T X^T X \hat{\beta}}\begin{bmatrix} c_1 \\ c_2 \end{bmatrix} \begin{bmatrix} \hat{\beta}_1 & \hat{\beta_2} \end{bmatrix} \]
A conta acima gera uma matriz com dois candidatos a estimador, um com constante \(c_1\) e outro com constante \(c_2\). Novamente, \(\hat{\beta}^T X^T X \hat{\beta}\) é um número, não uma matriz. O estimador não faz encolhimento do intercepto (eu não vou dar nenhuma explicação para isso, mas o glmnet também não encolhe o intercepto).
O próximo passo é simular o EQM para um valor do parâmetro. Nós vamos computar o valor esperado do EQM simplesmente simulando um número \(p\) de modelos e tirando a média - noutras palavras, um Monte Carlo:
monte_carlo_loss <- function(true_par,regs,n,k,p){
input <- replicate(p,true_par,simplify = F)
output <- map(input,simul_various_regs,regs = regs,n = n,k = k)
cofs <- c(0,rep(true_par,k))
true_par_mat <- t(replicate(length(regs)+1,c(cofs)))
loss <- map(output,function(x){(x-true_par_mat)^2 %>% rowSums()})
loss <- do.call(rbind,loss) %>% colMeans()
return(loss)
}Eu uso o map no lugar de um for por motivos que o Pedro já expôs. O primeiro mapchama a função anterior para simular uma replicação do Monte Carlo. Cada simulação vai retornar uma matriz que tem o número de valores para \(c\) mais uma linhas e \(k+1\) colunas. O segundo map calcula a função perda para cada simulação. Como o resultado de cada simulação é uma matriz, eu crio a variável true_par_matque arruma os valores verdadeiros do parâmetro em uma matriz.
A última função calcula o EQM para vários valores do parâmetro usando a função acima:
monte_carlo_pars <- function(true_pars,regs,n,k,p){
input <- as.list(true_pars)
output <- map(input,monte_carlo_loss,regs = regs,n=n,k=k,p=p)
result <- do.call(rbind,output)
rownames(result) <- true_pars
return(result)
}Vamos começar testando com \(k=5\) e \(c = 5-2 = 3\) e parâmetros de 0 a 4:
params <- seq(0,4,by=0.1)
teste <- monte_carlo_pars(params,3,100,5,1000)Cada coluna é a função perda para um estimador e cada linha varia o valor do parâmetro verdadeiro. Eu vou usar o pivot_longer do tidyr para deixar isso organizado como o ggplot precisa:
tidy_teste <- as_tibble(teste) %>%
rename("James-Stein"="3", "MQO" = ols) %>%
bind_cols(params = params) %>%
pivot_longer(!params)
ggplot(tidy_teste,aes(x=params,y=value,color=name)) +
geom_line() +
labs(x = "Parâmetro", y = "EQM", color = "Estimador") +
theme_light()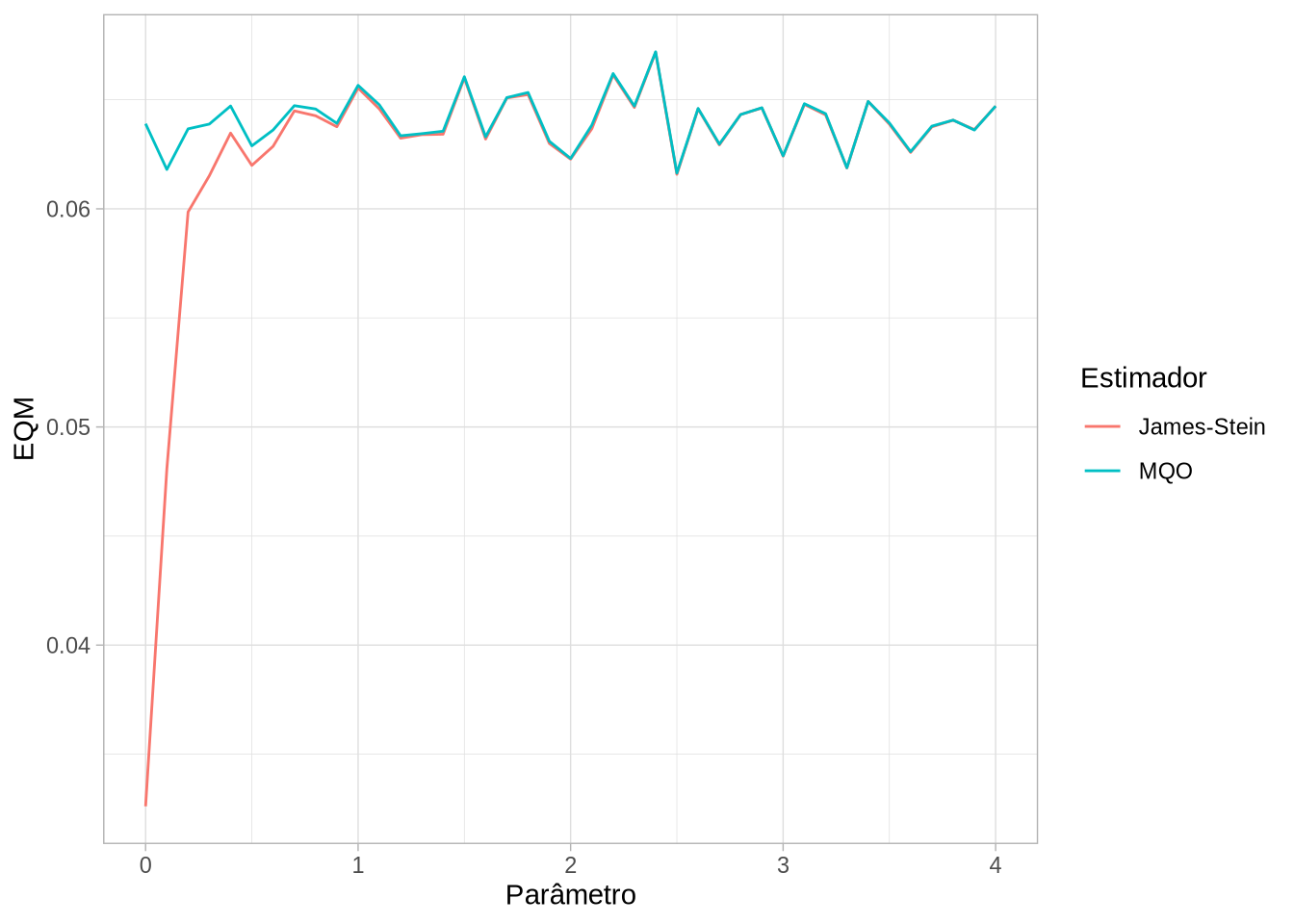
O estimador faz exatamente o prometido: ele nunca tem um EQM pior que os mínimos quadrados e é melhor que o estimador de MQO para um intervalo.
Isso significa que o estimador de MQO é inadmissível. Mas:
- O estimador James-Stein é viesado
- Ele depende de uma forma quadrática dos parâmetros de mínimos quadrados (\(\hat{\beta}^t X^t X \hat{\beta}\))
Veja que o ponto 2 não é nenhum problema (computacional, pelo menos). O ponto 1 é um pouco mais preocupante, especialmente se seu interesse é interpretar o coeficiente como um efeito de tratamento. Mas isso ilustra que, para previsão, mínimos quadrados não é necessariamente ótimo.
Veja que isso é uma motivação para estimadores de encolhimento em geral porque o estimador James-Stein faz encolhimento. Veja a fórmula:
\[ \hat{\beta}_{JS} = \hat{\beta}_{MQO} - \frac{c\sigma^2}{\hat{\beta}_{MQO}^T X^{T} X \hat{\beta}_{MQO}} \hat{\beta}_{MQO} \]
Se o estimador é positivo, você está subtraindo um valor dele; se o estimador é negativo, você está somando (porque \(\hat{\beta}_{MQO}\) é negativo). Qualquer que seja o valor estimado, o estimador James-Stein aproxima ele de zero… O que é extremamente parecido com que LASSO, Ridge, adaLASSO fazem.
Agora vamos ver o ponto 2, que para o modelo com erros normais, nós temos que \(k-2\) é o melhor valor para \(c\). Eu vou focar em \(k=5\) porque cada simulação demora um tempo. Neste caso, o ótimo é \(c=3\) Eu vou focar só nos valores do parâmetro pertos de 0 porque a simulação anterior mostrou que para valores grandes o parâmetro converge para o valor de MQO2.
params <- seq(0,1,by=0.1)
regs <- seq(1,5,by=1)
teste <- monte_carlo_pars(params,regs,100,5,1000)
tidy_teste <- as_tibble(teste) %>%
rename("MQO" = ols) %>%
rename_with(.fn = ~(paste0("c=",.)),.cols = matches("[[:digit:]]")) %>%
bind_cols(params = params) %>% pivot_longer(!params)
ggplot(tidy_teste,aes(x=params,y=value,color=name)) +
geom_line() + labs(x = "Parâmetro", y = "EQM", color = "Estimador") +
theme_light() +
scale_color_brewer(palette = "Dark2")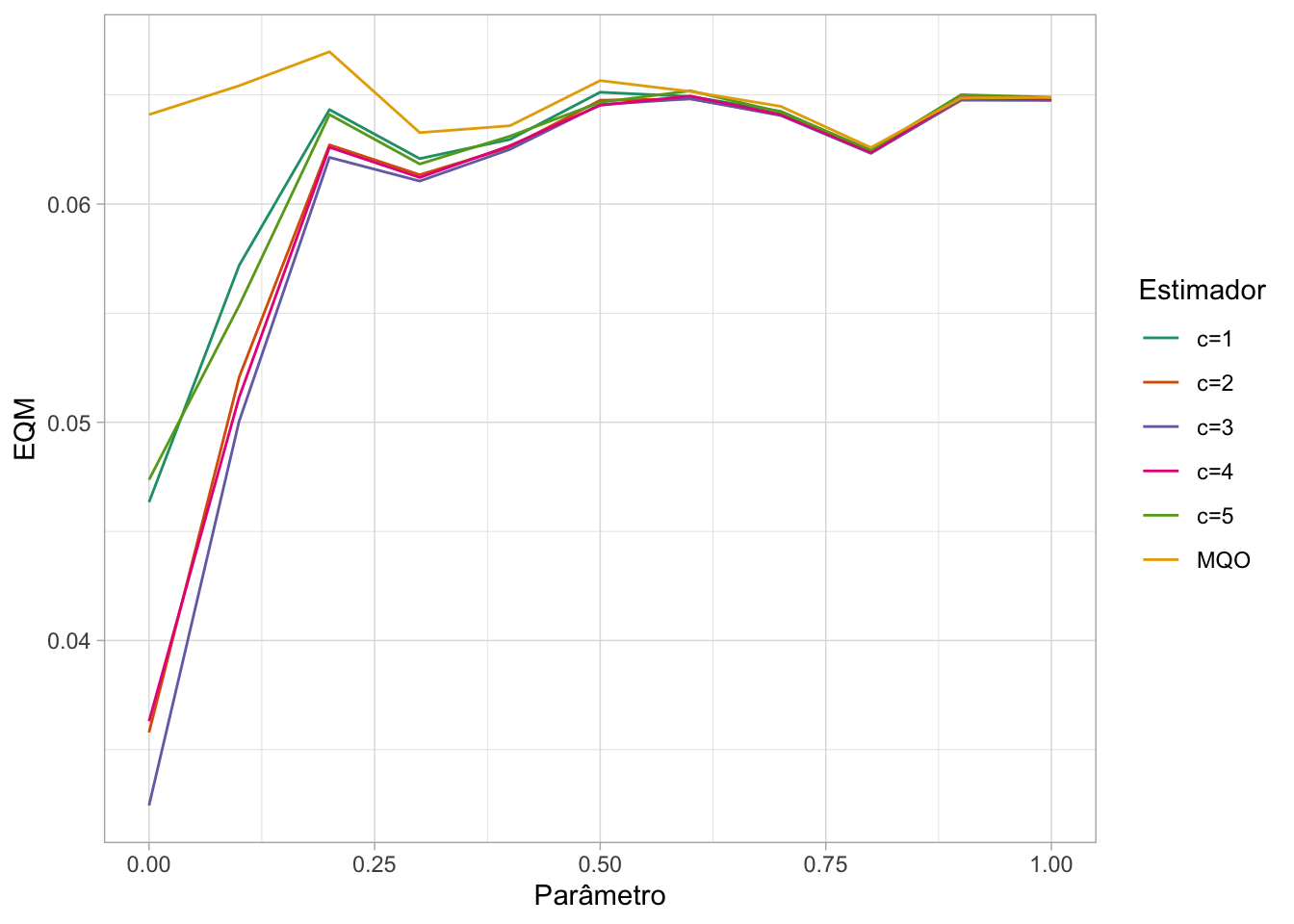
A linha mais embaixo - e portanto com menor EQM - é a associada com \(c=3\), como a teoria manda.
Este é um destes posts que começam com um tema meio abstrato (teoria da decisão) e desaguam em um resultado completamente maluco (MQO é inadmissível). A gente nem precisou fazer conta nenhuma, o computador fez tudo. Eu não fiz essas contas para o LASSO porque senão o post ia se esticar ainda mais.
Bibliografia
O capítulo 7 do Computer Age Statistical Inference discute exatamente o estimador James-Stein, dando uma motivação Bayesiana. A fórmula que eu usei no post pro estimador James-Stein veio de lá. A discussão está mais próxima do Econometric Foundations, apesar de eu ter sérias dúvidas sobre a fórmula do estimador James-Stein que está no livro.