Viés em Diferenças em Diferenças

Sim, eu nunca achei que eu ia chegar a isso. Mas cá estamos: um post sobre viés em diferenças em diferenças. Esse é um tópico relativamente falado em econometria e com uns exemplos legais, então eu decidi fazer esse post.

Sempre que a gente tem dados em painel, a reação pavloviana é dizer “efeitos fixos”. A ideia é que efeitos fixos capturam a heterogenidade não observada e isso potencialmente resolve problemas de viés de seleção.

O problema é quando nem todo mundo é tratado ao mesmo tempo. Curiosamente, o efeito fixo usual não funciona nesse caso - ou seja, o estimador é viesado. Mas a solução é extremamente simples e nos lembra que nem sempre o estimador usual funciona, mas uma pequena variação pode funcionar.

Se você precisa de um exemplo de tratamento que não é todo mundo ao mesmo tempo, talvez o melhor exemplo seja vacinação de covid: primeiro, os mais idosos foram vacinados e os mais jovens foram vacinados meses depois.

Para entender o problema, a gente vai fazer simulações - previsivelmente. A gente vai usar a linguagem de potential outcome aqui e então seja a variável de tratado ou não $D$, o resultado se for tratado $Y(1)$ e se não for tratado $Y(0)$ e a gente observa:

$$Y = DY(1) + (1-D)Y(0)$$

O efeito de tratamento é $Y(1) - Y(0)$ e a gente só observa $Y$. Como a gente está simulando, a gente pode salvar o efeito do tratamento salvando $Y(1)$ e $Y(0)$. Dos muitos efeitos de tratamento possíveis, diferenças em diferenças recupera o efeito de tratamento sobre os tratados.

A gente vai usar o R pra aproveitar o pacote plm e eu vou usar paralelização porque eu sou impaciente:

library(plm)
library(purrr)
library(dplyr)
library(ggplot2)
library(furrr)
library(tidyr)

plan(multisession,workers = 8)

set.seed(25122023)

Eu nunca tinha feito nenhuma simulação gerando dados em painel - mentira, eu fiz uma vez na graduação, então não conta. Eu pensei bastante em como estruturar isso e achei melhor quebrar em uma função que gera dados pra um indíviduo e uma função que gera o painel a partir dessa função. Primeiro, a função que gera dados pra um indivíduo. A função vai ter vários inputs: um id, que diz qual o número que identifica o indvíduo; t me diz quantos períodos eu observo; common shock é só um choque em comum pra todos os indvíduos na hora que eu gerar o painel, e que vai ser responsabilidade do efeito fixo de tempo de remover; cohort é a coisa crítica aqui e me diz quando o indivíduo vai ser tratado se ele for tratado; treat_effect é o tamanho do efeito de tratamento, que é o que nos interessa; thres requer um pouquinho mais de explicação. A gente vai adotar o seguinte esquema: se uma variável aleatória $u$ estiver acima de thres, a unidade é tratada; senão, a unidade não é tratada. A gente assume que $u$ não é observado:

one_indv <- function(id,t,common_shock,cohort,treat_effect,thres){
  if(cohort > t){
    stop("Cohort higher than number of periods")
  }
  
  if(cohort == 0){
    cohort <- t + 1
  }
  
  u <- rnorm(1)
  
  treat <- u > thres
  
  y0 <- common_shock + rep(u,t+1) + rnorm(t+1)
  y1 <- rep(treat_effect,t+1) + rep(u,t+1) + rnorm(t+1) + common_shock
  
  time_grid <- 0:t
  treated <- (time_grid >= cohort)*treat
  y <- y0*(1-treated) + y1*treated
  
  dataframe <- data.frame("id" = rep(id,t+1), "T" = time_grid, "D" = treated, "Y" = y, "Y0" = y0, "Y1" = y1)
  
  return(dataframe)
  
}

Da maneira que o código está escrito, tem duas maneiras de não ser tratado: ou a sua cohort é zero ou a sua variável $u$ está abaixo do limiar. Eu vou escrever a função que gera o painel de maneira que ninguém nunca tem cohort = 0:

panel1 <- function(t,n,thres,treat_effect){
  
  v <- 0:t
  cohort <- sample(1:t,n,replace = TRUE)
  panel_list <- map(1:n,\(x)one_indv(x,t,v,cohort[x],1,thres))
  panel <- do.call(rbind,panel_list)
  panel <- as.data.frame(panel)
  
  return(panel)
  
}

Da maneira que painel1 está escrito, todo mundo tem o mesmo thres e o mesmo efeito de tratamento. Isso não é ruim porque tira uma variação e permite a gente focar na variação de ter vários períodos. Vamos olhar o que acontece quando a gente roda isso uma vez, com 4 períodos e 500 indivíduos:

data <- panel1(3,500,0,1)
mod <- plm(Y ~ D,data = data, index = c("id","T"),effects = "twoways")
data_treated <- data %>% group_by(id) %>% filter(D == 1)
ATT <- data_treated$Y1 - data_treated$Y0

O efeito de tratamento é a média da variável ATT, que é 1.1543809 e é bem perto do que a gente colocou no código. O efeito de tratamento estimado é 3.1549142, que é o dobro do valor verdadeiro.

Vamos fazer umas mil simulações pra ver o que acontece. Eu vou escrever uma função que me retorna o efeito de tratamento e o coeficiente estimado e ai eu vou usar o map paralelizado, future_map pra fazer as simulações multicore (no ano 2023, quem tem tempo para rodar as simulações sem ser em paralelo?):

simul1 <- function(t,n,thres,treat_effect){
  data <- panel1(t,n,thres,treat_effect)
  mod <- plm(Y ~ D,data = data, index = c("id","T"),effects = "twoways")
  data_treated <- data %>% group_by(id) %>% filter(D == 1)
  ATT <- data_treated$Y1 - data_treated$Y0
  
  return(c(coef(mod),mean(ATT)))
}

resul <- future_map(1:1000,\(x)simul1(3,500,0,1), .options = furrr_options(seed = TRUE))
resul <- do.call(rbind,resul)

diff <- resul[,1] - resul[,2]

Vamos fazer um histograma disso:

ggplot(data.frame(var = diff),aes(var)) + geom_histogram() + theme_light() + labs(x = "Diferença entre estimado e ATT")

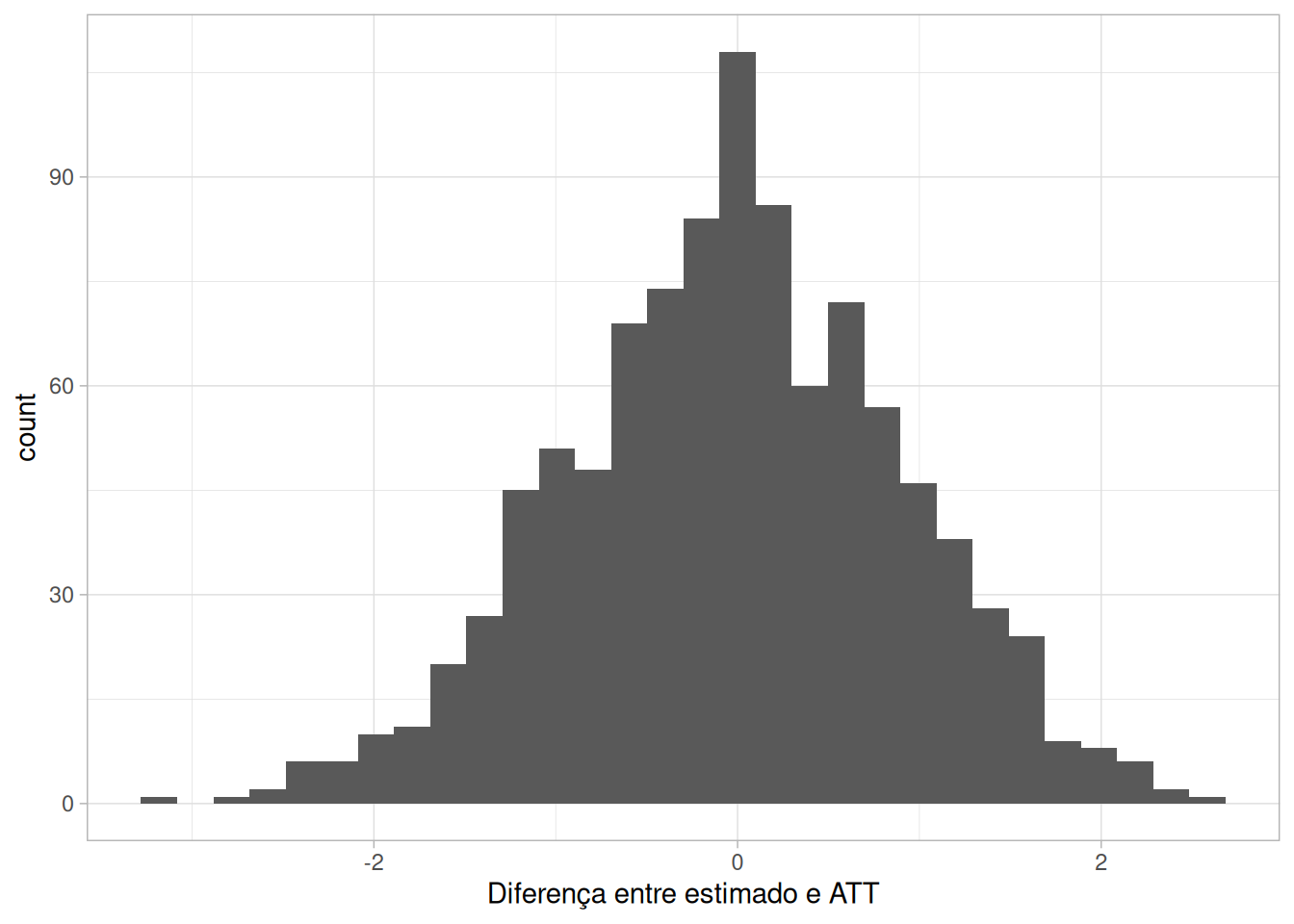
Tudo parece bem aqui: o histograma está centrado em zero e parece ter só uma pequena assimetria. O problema maior é quando a gente tem efeitos de tratamento que mudam conforme a data que o indivíduo é tratado. A gente vai alterar um pouquinho a função painel1 pra permitir diferentes efeitos de tratamento em cada período e diferentes probabilidades de ser alocado a cada período (é pra isso que a gente tem um novo argumento na função, prob):

panel2 <- function(t,n,thres,treat_effect,prob){
  
  v <- 0:t
  cohort <- sample(1:t,n,replace = TRUE,prob = prob)
  treat_effect_n <- treat_effect[cohort]
  panel_list <- map(1:n,\(x)one_indv(x,t,v,cohort[x],treat_effect_n[x],thres))
  panel <- do.call(rbind,panel_list)
  panel <- as.data.frame(panel)
  
  return(panel)
  
}

Vamos fazer igualzinho acima:

treatment_effects <- c(1,2,3)
data <- panel2(3,5000,0,treatment_effects,c(1/4,1/4,3/8))
mod <- plm(Y ~ D,data = data, index = c("id","T"),effects = "twoways")
data_treated <- data %>% group_by(id) %>% filter(D == 1)
ATT <- mean(data_treated$Y1 - data_treated$Y0)

O efeito de tratamento é a média da variável ATT, que é 1.7545035, enquanto o efeito de tratamento estimado é 4.1412855. Vamos criar outra função que faz a simulação:

simul2 <- function(t,n,thres,treat_effect,prob){
  
  data <- panel2(t,n,thres,treat_effect,prob)
  mod <- plm(Y ~ D,data = data, index = c("id","T"), effect = "twoways")
  data_treated <- data %>% group_by(id) %>% filter(D == 1)
  ATT <- mean(data_treated$Y1 - data_treated$Y0)
  
  return(c(coef(mod),mean(ATT)))
  
}

treatment_effects <- c(3,2,1)

resul2 <- future_map(1:1000,\(x)simul2(3,500,0,treatment_effects,c(1/4,1/4,3/8)), .options = furrr_options(seed = TRUE))
resul2 <- do.call(rbind,resul2)

diff2 <- resul2[,1] - resul2[,2]

ggplot(data.frame(var = diff2),aes(var)) + geom_histogram() + theme_light() + labs(x = "Diferença entre estimado e ATT")

O efeito de tratamento estimado não está centrado em 0. Na média o nosso viés é negativo, então a gente está subestimando o efeito de tratamento verdadeiro.

Como resolver isso? O problema é que a gente está trabalhando com as variáveis erradas. Na regressão, a gente está definindo um único efeito de tratamento. Mas, o código que simula usa diferentes efeitos de tratamento. Então, até do ponto de vista de recuperar os efeitos de tratamento, nós gostaríamos de recuperar o efeito de tratamento para quem é tratado no período 1 em diante, do período 2 em diante etc. O que acontece é que o estimador de diferenças em diferenças usual faz uma combinação linear desses efeitos de tratamento que não necessariamente somam um nem são positivas, então a gente obtém um estimador que não faz sentido:

simul3 <- function(t,n,thres,treat_effect,prob){
  
  data <- panel2(t,n,thres,treat_effect,prob)
  data <- data  %>% group_by(id) %>% mutate(cohort = (t+1) - sum(D),Dd = cohort*D) %>% mutate(cohort = as.factor(cohort),T = as.factor(T), Dd = as.factor(Dd)) %>% mutate(cohort = relevel(cohort,"4"))
  mod <- lm(Y ~ Dd + cohort +T,data = data)
  data_treated <- data %>% group_by(id) %>% filter(D == 1)
  ATT <- mean(data_treated$Y1 - data_treated$Y0)
  
  return(c(coef(mod)[c("Dd1","Dd2","Dd3")],mean(ATT)))
  
}

Vamos fazer a simulação:

resul3 <- future_map(1:1000,\(x)simul3(3,500,0,treatment_effects,c(3/8,3/8,2/8)), .options = furrr_options(seed = TRUE))

Agora a gente tem três efeitos de tratamento, vamos ver qual a média:

resul3 <- do.call(rbind,resul3)
colMeans(resul3[,1:3])

##       Dd1       Dd2       Dd3 
## 2.9996215 1.9975379 0.9994349

Vamos fazer um histograma, e pra ficar fácil de vizualizar eu vou plottar desvios do efeito de tratamento estimados dos efeitos de tratamento que a gente estabeleceu no código:

true_effect <- matrix(treatment_effects,nrow=1000,ncol=3,byrow = TRUE)

est <- resul3[,1:3] - true_effect %>% as.data.frame()
est <- pivot_longer(est,everything())

ggplot(est,aes(value)) + geom_histogram() + facet_grid(.~name) + theme_light()

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.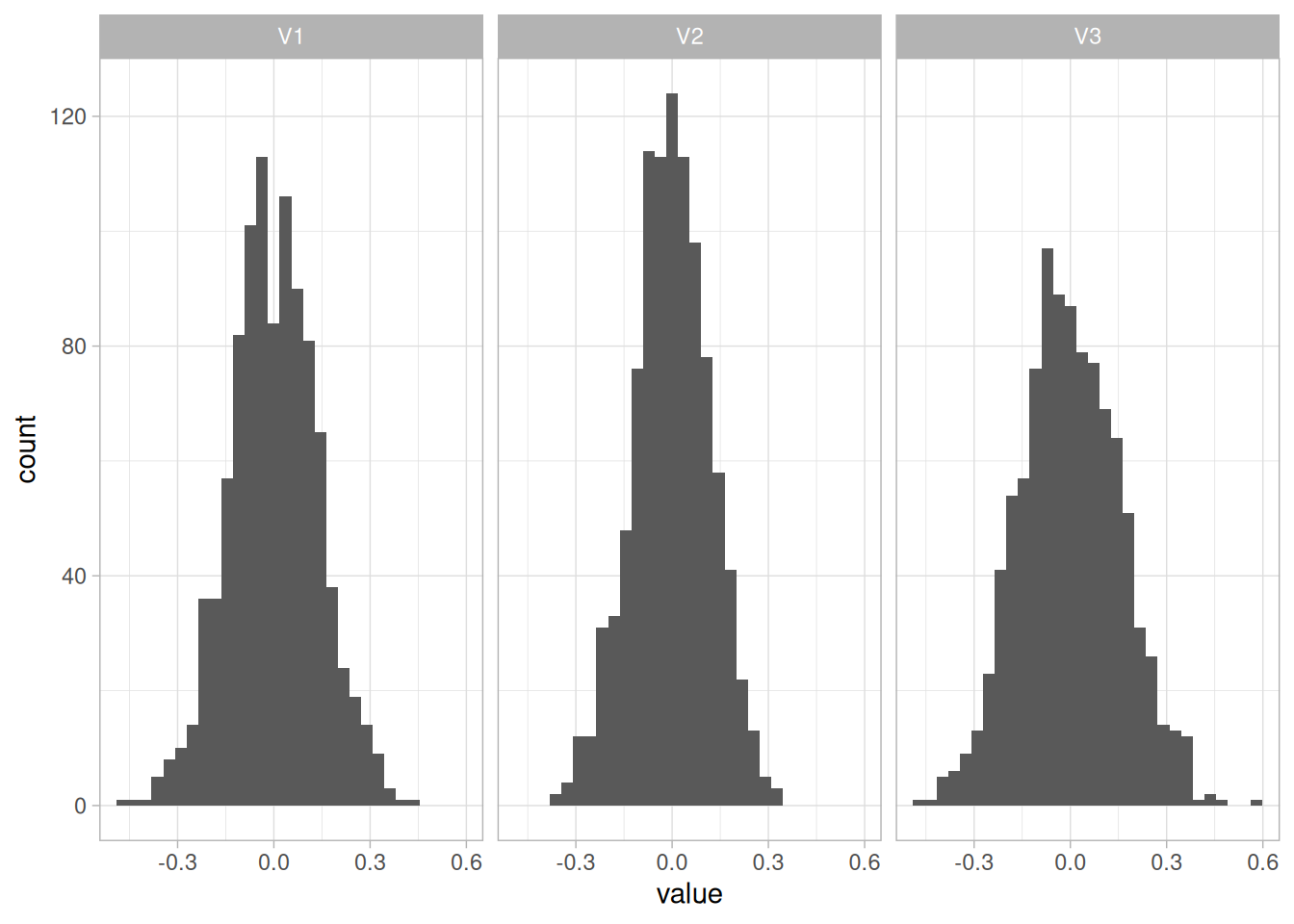

A média dos efeitos de tratamento pra cada coorte é bem próximo do que a gente estabeleceu e os histogramas são bem comportados. É fácil a gente construir qualquer estimador a partir disso,por exemplo, a gente pode fazer uma média ponderada pela probabilidade de pertencer a cada coorte. Isso exigira reescrever o código um pouquinho porque nenhuma das funções entrega a proporção em cada coorte. Esse post já está longo o bastante e então fica como exercício para o leitor.

É claro, nada desse post é original: o problema é do paper do Chaisemartin (Two-Way Fixed Effects Estimators with Heterogeneous Treatment Effects) e a solução veio de um paper do Wooldridge.