O LASSO

Este post vai tratar de um método de machine learning muito interessante e relativamente simples: o LASSO. LASSO significa Least Absolute Shrinkage and Select Operator. Como o nome sugere, o LASSO seleciona quais regressores são relevantes e quais não são. Ou seja, suponha que você é um pesquisador que tem 50 variáveis que são possíveis candidatos a variáveis explicativas de uma variável de interesse. O LASSO permite que você dê os 50 regressores para o computador e ele escolha quais são os relevantes. O LASSO está centrado na ideia de esparsidade: poucos coeficientes vão ser diferentes de zero; poucas variáveis vão ser relevantes numa regressão.

Uma pergunta justa é: por que não simplesmente testamos isso “na mão”? Isso é, fazemos uma regressão com todas as variáveis, uma sem a primeira variável da base de dados, uma outra sem a segunda… e no fim vemos qual a melhor regressão? Além de problemas de teste - lembre que todo teste tem uma chance de você estar tomando a decisão errada - isso seria um inferno: com relés 50 variáveis, precisaríamos de $2^{50}$ regressões, ou seja, 1.1258999^{15} regressões: esse é um número com 15 zeros.

A ideia original vem de um paper de 1996 de Robert Tibshirani. Não temos solução fechada para encontrar o estimador de LASSO, ao contrário do MQO, onde podemos expressar o estimador como uma multiplicação de matrizes. Portanto, é um estimador que seria impossível sem um computador. Mas a ideia é incrivelmente simples.

Pegue o modelo usual de regressão, $y_i = X_i \beta + u_i$, onde $\beta$ é o coeficiente de interesse, $u$ é um choque aleatório, as observações são indexadas por $i = 1,...,n$ e os coeficientes são indexados por $k = 1,..,K$ . O objetivo do MQO é minimizar a soma dos quadrados dos resíduos, ou seja $\min_{\beta} \sum_{i=1}^n \hat{u}^2$. O LASSO começa dai, mas adiciona uma pequena alteração: vamos limitar o valor da soma dos valores absolutos dos coeficientes para que ele seja menor que uma constante $c$. Ou seja, o LASSO resolve o problema:

$$\min_{\beta} \sum_{i=1}^n \hat{u}^2 \text{ sujeito a } \sum_{k=1}^K |\beta_{k}| < c$$

Veja que não temos como tirar a derivada da função módulo, e portanto não podemos resolver o problema “no braço”.

Podemos reescrever o problema como um la grangeano: $\min_{\beta} \left( \sum_{i=1}^n \hat{u}^2 \right) - \lambda \left( \sum_{k=1}^K |\beta_{k}| \right)$, onde o $\lambda$ é o multiplicador de lagrange. Existe uma função que leva de $c$ para $\lambda$, então podemos ignorar o valor de $c$ e pensar só em termos de $\lambda$. Muitas implementações fazem isso e eu seguirei este caminho.

Veja que estamos trabalhando a soma do valor absoluto dos coeficientes. Chamamos isso de norma $\ell_1$. Aqueles que já fizeram um curso de algebra linear conhecem a norma $\ell_2$, conhecida como norma euclidiana: $\sum_{k=1}^K \beta{}^2$. Existe um método de estimação que usa a norma $\ell_2$ ao invés da $\ell_1$, conhecido como ridge. Usando a norma $\ell_2$, o problema tem solução analítica. Então, por que norma $\ell_1$, que parece ser tão ruim de trabalhar?

Esta é uma das belezas do LASSO: a norma $\ell_2$ não gera esparsidade. A norma $\ell_1$ gera. O motivo é ilustrado na figura abaixo, tirada de Statistical Learning with Sparsity, de Trevor Hastie, Robert Tibshirani and Martin Wainwright (cujo pdf, 100% legal, você encontra aqui)

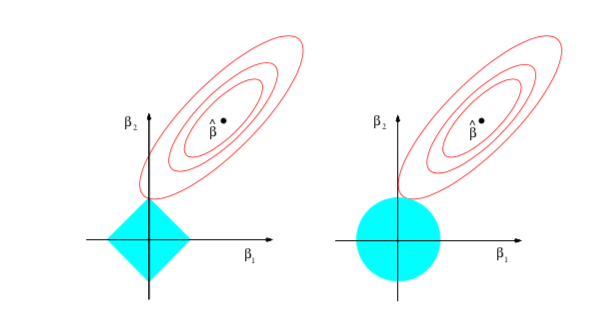
A imagem supõe que você só tem duas variáveis, por motivos ilustrativos. O $\hat{\beta}$ é o máximo global, o conhecido estimador de MQO. Em vermelho são as curvas de nível do estimador. O que o Ridge (à direita) faz é impor uma restrição no formato de uma bola (azul). Veja que a curva de nível encosta na bola fora do eixo vertical - onde $\beta_1$ seria zero. Já o LASSO é ilustrado na figura à esquerda. Veja que, nesse caso, a curva de nível acerta na quina da restrição, efetivamente zerando o coeficiente $\beta_1$.

Veja que, por enquanto, eu escondi o $\lambda$ (ou o $c$) debaixo do tapete: eu ainda não expliquei como escolher essa variável, que de fato está no centro do problema. O pesquisador pode ter uma vaga ideia de quanto os coeficientes devem somar. Mas uma ideia exata do tamanho é complicada, então gostariamos de deixar os dados nos dizerem o $\lambda$ certo. Existem várias estratégias, e infelizmente o glmnet só implementa uma.

Com alguma ideia do que o LASSO está fazendo, podemos colocar a mão na massa e discutir o pacote padrão para o LASSO no R, o glmnet.

##O pacote glmnet

Obviamente, começamos carregando o pacote:

library(glmnet)

## Carregando pacotes exigidos: Matrix

## Loaded glmnet 4.0-2

O comando para rodar uma regressão usando o LASSO é o glmnet. Ele recebe basicamente duas coisas, uma matriz com regressores e o vetor que é a variável dependente. Até ai, muito parecido com o MQO. Mas a grande diferença em termos de output é que o glmnet devolve uma matriz de coeficientes. O que o glmnet faz é estimar o modelo para um vetor de $\lambda$, de tal forma que você vá de nenhuma variável incluida no modelo até todas as variáveis. Isso não significa que cada $\lambda$ estimado adicione uma variável nova ao modelo: em alguns casos o LASSO não seleciona mais ninguém, mas como ele tem mais “orçamento” para alocar, ele aumenta o valor dos coeficientes das variáveis incluídas. O glmnet resolve o problema de escolher qual $\lambda$ usar simplesmente estimando com vários valores diferentes.

Vamos testar o glmnet gerando uma matriz com 50 variáveis e 2000 observações e criando uma variável dependente que depende só das 10 primeiras variáveis:

x <- matrix(rnorm(2000*50), ncol = 50) #regressores
betas <- c(rep(1,10),rep(0,40)) # as 10 primeiras serão relevantes com um coeficiente 1. As outras são irrelevantes - e portanto tem um coeficiente 0
y <- x%*%betas + rnorm(2000) 

modelo <- glmnet(x,y)
coef(modelo)[,1:5] # só pegando as 5 primeiras colunas. Veja que o comando summary não nos dá o que queremos no glmnet

## 51 x 5 sparse Matrix of class "dgCMatrix"
##                    s0          s1         s2         s3         s4
## (Intercept) 0.0899452 0.088733817 0.08744122 0.07980104 0.07205909
## V1          .         .           0.07186523 0.15461998 0.22925068
## V2          .         0.006269833 0.09268133 0.17163545 0.24390558
## V3          .         .           .          0.04081292 0.12344005
## V4          .         0.023074549 0.10526749 0.18520641 0.26065968
## V5          .         .           .          0.08775326 0.16789139
## V6          .         .           0.05578103 0.13964770 0.21611625
## V7          .         .           0.01023765 0.09799273 0.17949380
## V8          .         0.095583403 0.17473050 0.24967983 0.32036144
## V9          .         .           0.04487896 0.12992889 0.20907527
## V10         .         .           .          0.06677614 0.14574878
## V11         .         .           .          .          .         
## V12         .         .           .          .          .         
## V13         .         .           .          .          .         
## V14         .         .           .          .          .         
## V15         .         .           .          .          .         
## V16         .         .           .          .          .         
## V17         .         .           .          .          .         
## V18         .         .           .          .          .         
## V19         .         .           .          .          .         
## V20         .         .           .          .          .         
## V21         .         .           .          .          .         
## V22         .         .           .          .          .         
## V23         .         .           .          .          .         
## V24         .         .           .          .          .         
## V25         .         .           .          .          .         
## V26         .         .           .          .          .         
## V27         .         .           .          .          .         
## V28         .         .           .          .          .         
## V29         .         .           .          .          .         
## V30         .         .           .          .          .         
## V31         .         .           .          .          .         
## V32         .         .           .          .          .         
## V33         .         .           .          .          .         
## V34         .         .           .          .          .         
## V35         .         .           .          .          .         
## V36         .         .           .          .          .         
## V37         .         .           .          .          .         
## V38         .         .           .          .          .         
## V39         .         .           .          .          .         
## V40         .         .           .          .          .         
## V41         .         .           .          .          .         
## V42         .         .           .          .          .         
## V43         .         .           .          .          .         
## V44         .         .           .          .          .         
## V45         .         .           .          .          .         
## V46         .         .           .          .          .         
## V47         .         .           .          .          .         
## V48         .         .           .          .          .         
## V49         .         .           .          .          .         
## V50         .         .           .          .          .

Obviamente, ainda temos que selecionar qual dos modelos nós queremos. O pacote nos permite selecionar por Cross Validation (CV). Em linhas gerais, o que o Cross Validation faz é separar os dados em $k$ blocos - 5,10, ou até mesmo blocos de uma única observação (conhecido como leave one out). Depois, escolha $k-1$ blocos e estime o modelo usando o glmnet. Para avaliar qual $\lambda$ devemos usar, use o bloco que não foi usado para estimar para ver qual modelo gera o menor erro segundo alguma métrica (erro quadrático médio, por exemplo). O CV vai permitir com que cada bloco tenha uma chance de ser “fora da amostra”.

Isso pode parecer muito computacionalmente intensivo - e de fato é - mas a implementação do glmnet é tão eficiente que normalmente num piscar de olhos o modelo é estimado - no meu Dell Vostro de 2012 com i5, 6GB e Windows 10, o tempo é de apenas 0.19s. O comando que faz a seleção do $\lambda$ é o cv.glmnet. Vamos testar no exemplo acima:

cross_val <- cv.glmnet(x,y)

coef(cross_val)

## 51 x 1 sparse Matrix of class "dgCMatrix"
##                        1
## (Intercept) -0.001739634
## V1           0.937859461
## V2           0.930282416
## V3           0.908357779
## V4           0.977442350
## V5           0.929193703
## V6           0.942473364
## V7           0.953166419
## V8           0.991665138
## V9           0.960682012
## V10          0.896159947
## V11          .          
## V12          .          
## V13          .          
## V14          .          
## V15          .          
## V16          .          
## V17          .          
## V18          .          
## V19          .          
## V20         -0.010307812
## V21          .          
## V22          .          
## V23          .          
## V24          .          
## V25          .          
## V26          .          
## V27          .          
## V28          .          
## V29          .          
## V30          .          
## V31          .          
## V32          .          
## V33          .          
## V34          .          
## V35          .          
## V36          .          
## V37          .          
## V38          .          
## V39          .          
## V40          .          
## V41          .          
## V42          .          
## V43          .          
## V44          .          
## V45          .          
## V46          .          
## V47          .          
## V48          .          
## V49          .          
## V50          .

O LASSO com CV põe apenas um coeficiente a mais. O cv.glmnet também fornece um plot com o número de coeficientes e o erro médio do Cross Validation, o que ajuda a ilustrar o ponto:

plot(cross_val)

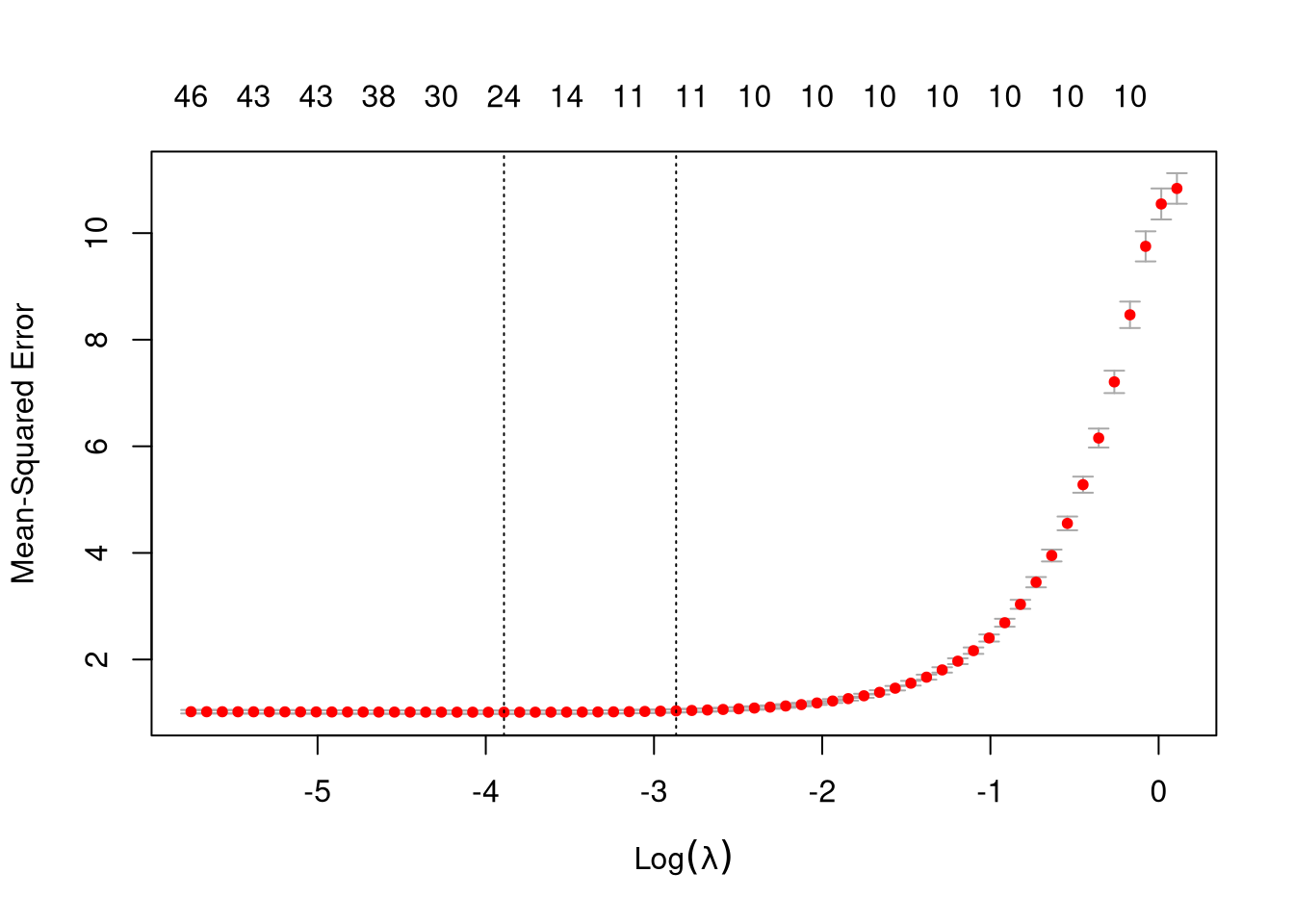
Uma das linhas tracejadas marca o número de coeficientes escolhidos: 11, número em cima. Depois dessa linha tracejada, o Mean Square Error não flutua muito. E também não há muita variação para imediatamente a direita, onde temos o modelo verdadeiro com 10 coeficientes.

(O autor agradece aos Professores Marcelo Medeiros e Pedro Souza pelas longas explicações sobre o LASSO e métodos correlatos. Pedro Cava, o outro autor deste blog, foi primordial em incentivar esse texto. Todos os erros neste texto são, como de praxe, de minha exclusiva culpa)