Identificação em VAR e Price Puzzle I

O VAR (Vector Autoregression, em inglês; em tradução livre, autoregressão vetorial) é um método padrão em estudos empíricos em macroeconomia. VARs são simplesmente empilhamentos de variáveis nas quais estimamos uma autoregressão. Para solidificar a ideia, suponha que temos duas variáveis \(x_t,y_t\) em um vetor \(\mathbf{x_t} = (x_t \phantom{0} y_t)'\). Um VAR seria:

\[\mathbf{x_t} = C\mathbf{x_{t-1}} + \mathbf{u_t}\]

Onde \(C\) é uma matriz \(2 \times 2\) e \(\mathbf{u_t}\) é um vetor de choques, possivelmente correlacionados. Uma equação do VAR é uma das linhas da matriz. A primeira linha, por exemplo, tem a seguinte cara:

\[x_t = c_{11}x_{t-1} + c_{12}y_{t-1} + u_{1t}\]

Por enquanto só falamos de VARs que tem uma defasagem do vetor \(\mathbf{x_t}\). Podemos ter VARs de qualquer ordem: um VAR(2) depende de \(\mathbf{x_{t-1}}, \mathbf{x_{t-2}}\) etc - e teremos matrizes \(C_1\) e \(C_2\), uma para cada lag. Felizmente, é possível escrever qualquer VAR de ordem p como um VAR(1): no fim do post eu mostro como fazer isso. Selecionar a ordem do VAR não é trivial e normalmente é feito usando algum critério de informação. Mas podemos obter toda a intuição com um VAR(1).

Veja que podemos estimar a matriz \(C\) estimando cada uma das equações por MQO e obter:

\[x_t = \hat{c}_{11}x_{t-1} + \hat{c}_{12}y_{t-1} + \hat{u}_{1t}\]

E sobre condições bastante gerais, \(\widehat{C}\) vai ser consistente.

Se em equações cross-section o nosso interesse é em um coeficiente particular - que dá um efeito causal - em um contexto de VAR, temos interesse na dinâmica, ou seja, numa sequência de efeitos parciais de uma variável em outra. Em geral, a nossa pergunta é “Dado um choque exógeno na variável x no período t, como o sistema se comporta?”. Veja que temos que considerar que um choque em \(x_t\) pode afetar \(y_t\) de maneira defasada, atraves do coeficiente \(c_{21}\), que pode afetar \(x_t\) no outro período através de \(c_{12}\). Esta trajetória recebe o nome de Função de Resposta ao Impulso (FRI), ou em inglês Impulse Response Function (IRF).

Felizmente temos uma maneira fácil de encontrar a FRI. Veja que da equação de \(\mathbf{x_t}\), temos que

\[\mathbf{x_t} = C\mathbf{x_{t-1}} + \mathbf{u_t}\] \[\mathbf{x_{t+1}} = C\mathbf{x_{t}} + \mathbf{u_{t+1}} = C^2\mathbf{x_{t-1}} + C\mathbf{u_t} + \mathbf{u_{t+1}}\]

E continuando a iteração, descobrimos que o efeito de um choque em \(t\) no período \(t+h\) é \(C^h\). Veja que \(C^h\) é uma matriz e cada posição da matriz dá o efeito de um choque em alguma variável: a posição [1,1] dá o efeito de um choque na variável 1 sobre a variável 1; [1,2] o efeito de um choque na variável 2 sobre a variável 1; etc. Nosso interesse é em toda a sequência \(\left\{C^h\right\}_{h=0}^{T}\), onde \(T\) é algum período distante no tempo onde o choque não tem mais nenhum efeito sobre as variáveis.

Por enquanto, tudo muito fácil: temos um objeto bem definido, a FRI; e uma maneira de estimar este objeto que é relativamente simples, o estimador de MQO. Mas veja que eu permiti correlação entre os erro, o que não é interessante. De fato, gostaríamos de erros que tivessem interpretações diretas. Para deixar este ponto claro, vamos especializar o nosso VAR: suponha que o vetor \(\mathbf{x_{t}} = (y_t \phantom{0} \pi_t \phantom{0} i_t)^{\prime}\), onde os termos são, respectivamente, uma medida de crescimento do produto (para termos estacionariedade), inflação, e juros. Se tivessemos erros correlacionados, um choque na equação de inflação não tem uma interpretação clara: ele acarreta um choque em alguma das outras equações. Gostariamos de conhecer o efeito de um choque que afetasse somente a inflação. Podemos reescrever todo o sistema da seguinte forma:

\[B\mathbf{x_{t}} = A\mathbf{x_t} + \mathbf{e_t}\]

Onde agora \(\mathbf{e_t}\) são erros não correlacionados e \(C \equiv B^{-1}A\). Veja que este VAR é igualzinho ao que escrevemos lá na primeira equação deste post. Para diferenciar estas duas formas de escrever um VAR, chamamos a forma com o \(B\) na frente de forma estrutural, e a forma sem o \(B\) de forma reduzida.

Podemos pensar que \(B\) é só uma matriz que faz com que \(\mathbf{u_t} = B^{-1}\mathbf{e_t}\). Mas \(B\) também tem interpretação econômica: é a matriz que diz quais são os efeitos contemporâneos entre as variáveis. Por exemplo, qual o efeito do aumento do PIB hoje na taxa de juros? Etc. Com essa interpretação, fica claro que podemos deixar a diagonal principal de \(B\) ser 1. Veja que podemos reescrever a FRI como \(C^{h}B^{-1}\), e agora as repostas impulso tem uma interpretação clara: a matriz \(B^{-1}\) faz com que cada choque seja a respeito de uma determinada variável, sem implicar em um valor para qualquer outro choque.

Se \(B\) não tiver alguma estrutura muito particular, teremos problemas na hora de tentar estimar: se \(\pi_t\) causa \(y_t\) e \(y_t\) causa \(\pi_t\), teremos o clássico problema de identificação em sistemas de equações. Uma solução possível é achar algum instrumento, mas isso pode ser extremamente desafiador. Qual variável é causada exogenamente neste sistema? E será que ela tem uma correlação com a variável que nos interessa?

Uma solução padrão na literatura de VAR é impor que algumas variáveis não se afetam mutuamente. Por exemplo, podemos estabelecer que inflação causa mudança nos juros hoje, mas o efeito dos juros sobre a inflação é defasado. Isso recebe o chique nome de decomposição de Choleski. Mas não é nada além de impor algumas restrições sobre o sistema de efeitos que tem que ser zero. Essa não é a única maneira de impor restrições sobre a matriz \(B\), mas é uma das mais populares.

Vamos levar todo este papo aos dados, como de praxe.

##Um VAR para o Brasil

Vamos fazer um VAR para o Brasil no R. Eu vou usar o excelente pacotes BETS para obter os dados de taxa Selic, IPCA e do IBC-Br, um índice do BCB que é mensal que serve como proxy para o PIB. Os dados são mensais. Eu usarei o pacote dynlm para fazer a estimação do VAR. Existe um ótimo pacote que faz estimação do VAR direto, o vars. No código, eu uso ele para checar se tudo está funcionando direitinho (essa parte eu não reproduzi aqui, mas você encontra (https://github.com/danmrc/azul/blob/master/C%C3%B3digos/VAR.R)[aqui]). O expm permite fazer potenciação de matriz, que vai ser essencial na hora de calcular a FRI.

library(BETS)
library(dynlm)
library(expm)
library(vars)

ipca <- BETSget(13522, from="2003-01-01", to = "2017-12-31")
ibc_br <- BETSget(24364, to = "2017-12-31")
selic <- BETSget(4189,from="2003-01-01", to = "2017-12-31")

O IBC-Br só tem dados disponíveis a partir de 2003. Vamos fazer o plot das séries, mas antes definimos a variável def com as configurações default do plot do R para podermos retornar sem estresse para o default:

def <- par()

#par(mfrow = c(3,1))

plot(ibc_br, main = "IBC-Br")
grid(col = "grey")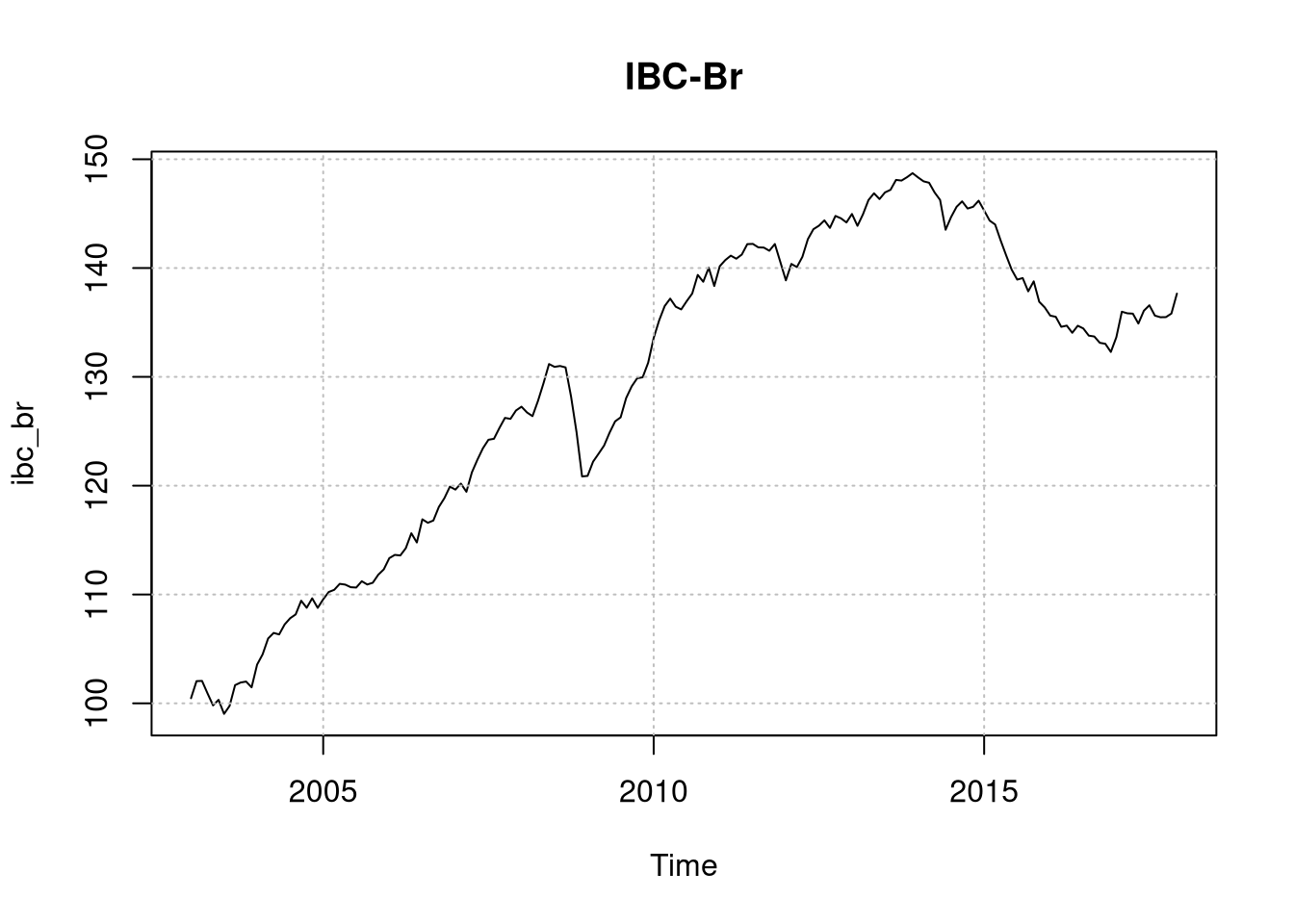

plot(ipca, main = "IPCA")
grid(col = "grey")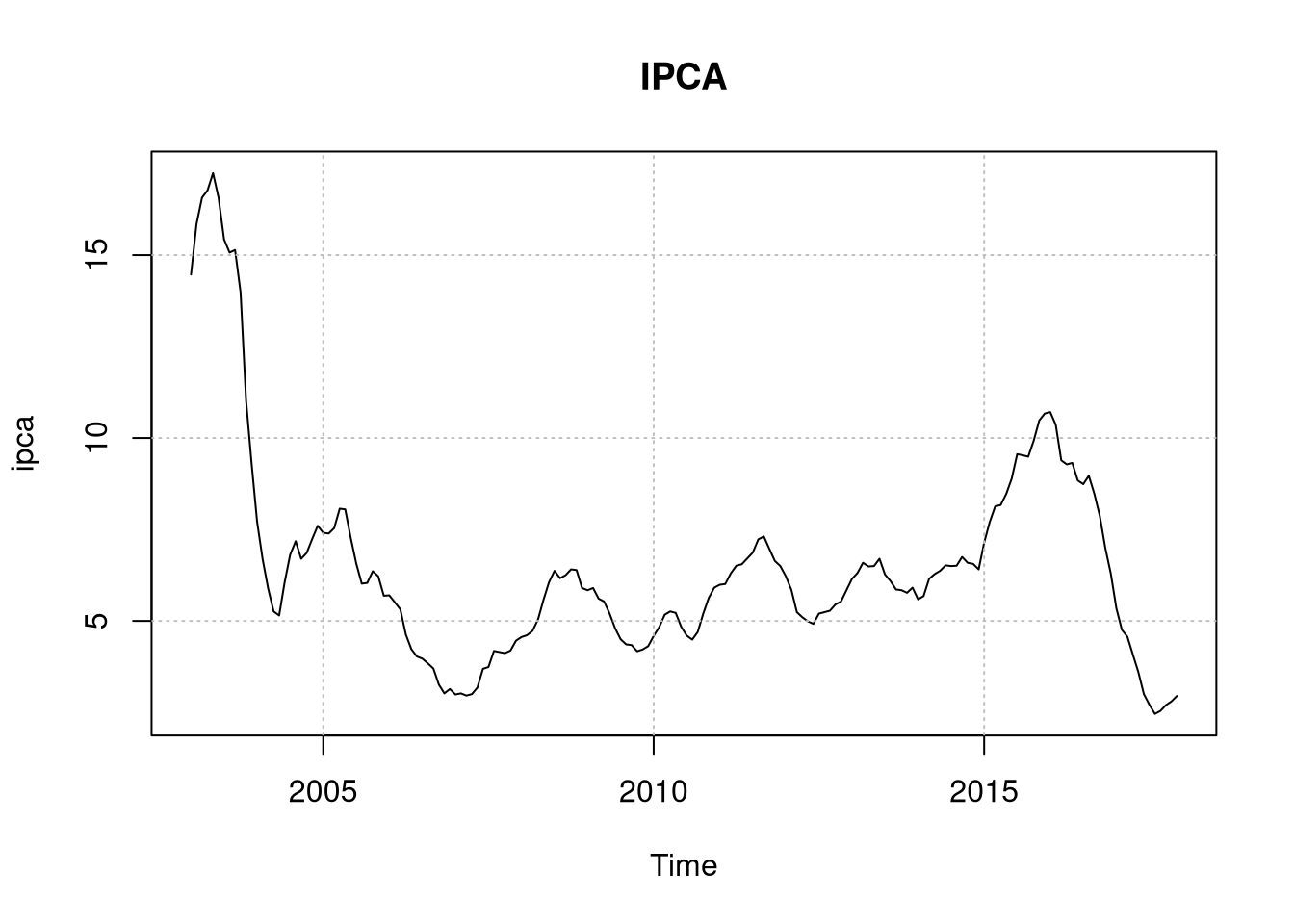

plot(selic, main = "Selic")
grid(col = "grey")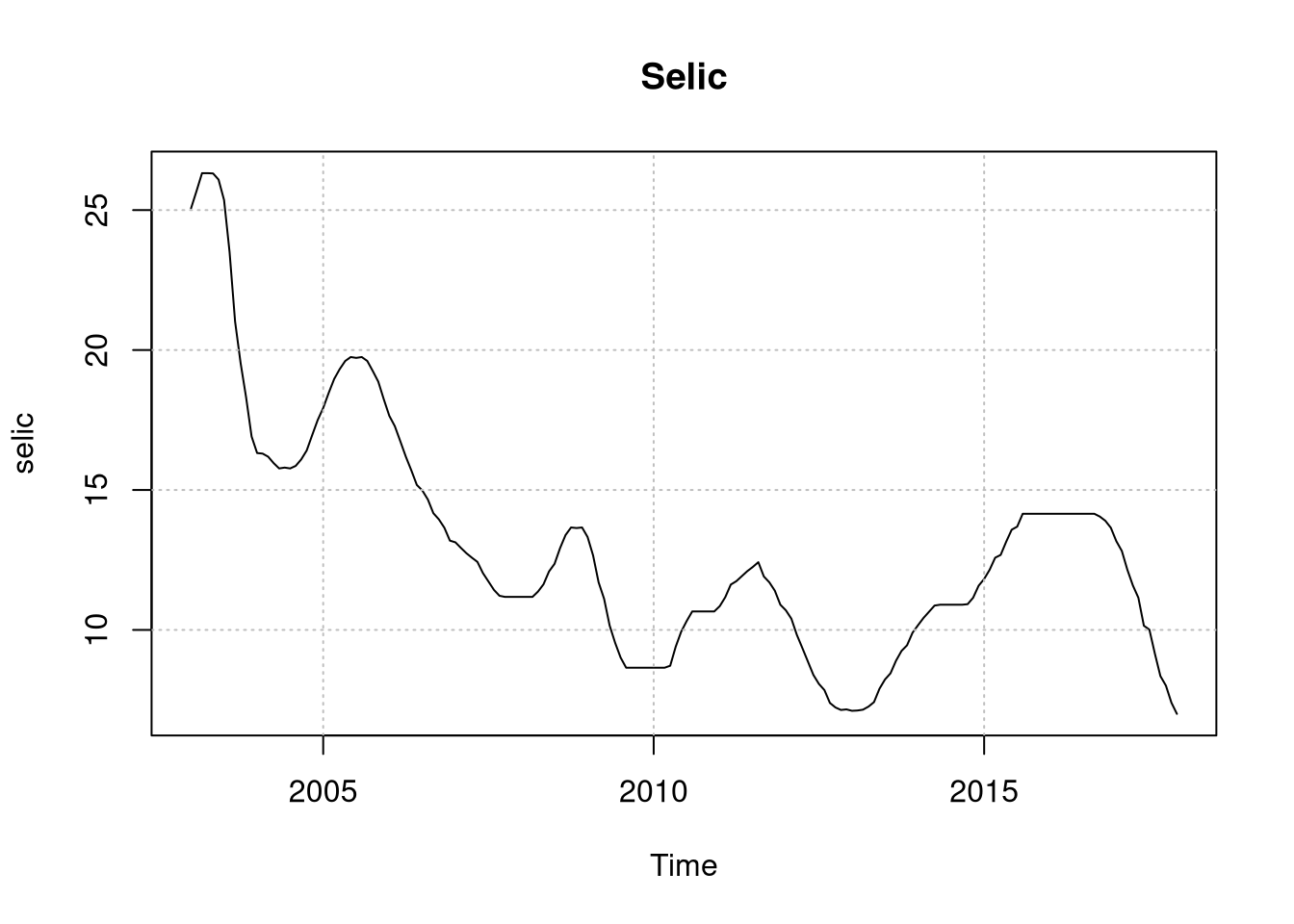

par(def)

Veja que par(mfrow = c(3,1)) permite com que eu plote as três séries uma debaixo da outra - eu desativei essa opção no post por motivos meramente estéticos, mas funciona muito bem usando a função zoom do RStudio e permite nós vermos as 3 séries uma embaixo da outra. Como esperado, a série do IBC é não estacionária. Vamos precisar deixar ela estacionária, e a solução óbvia é passar log e tirar a primeira diferença - obtendo assim a taxa de crescimento:

dibc <- diff(log(ibc_br))
ipca <- window(ipca, start = c(2003,02))
selic <- window(selic, start = c(2003,02))

Ao diferenciar, perdemos a primeira observação. O comando window limita as observações das outras séries para retirar a primeira observação. Vamos olhar a cara do crescimento do IBC:

plot(dibc)
grid(col = "grey")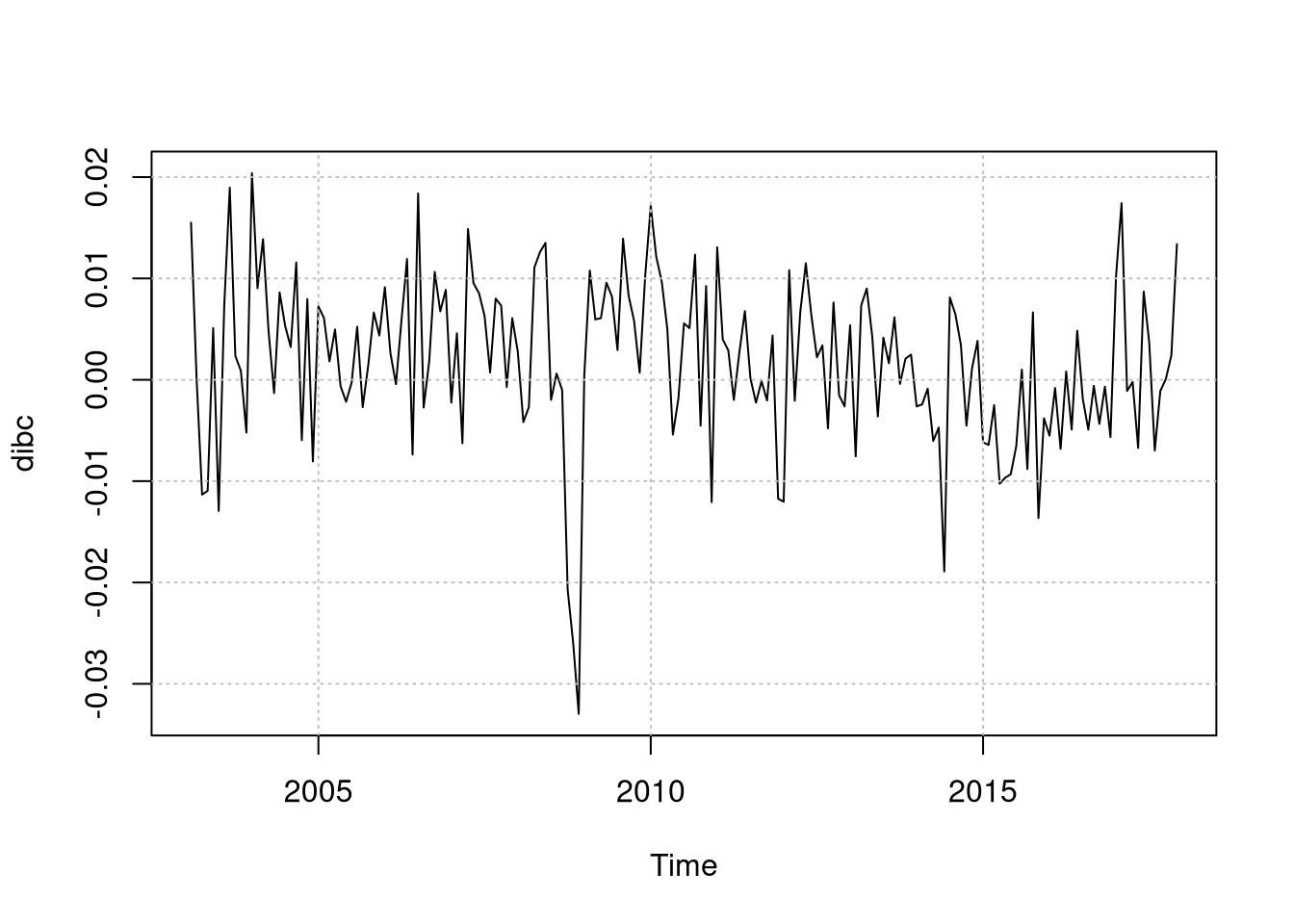

O pacote vars oferece o comando VARselect, que informa vários critérios de informação e quantos lags minimizam o critério. Vamos usar este comando para saber quantos lags devemos usar:

X <- cbind(selic,ipca,dibc)

VARselect(X)$selection

## AIC(n)  HQ(n)  SC(n) FPE(n) 
##      8      5      2      8

Eu vou ficar com o SBC (também conhecido como BIC), que sugere um modelo relativamente enxuto com 2 lags. Estimação de VAR é sempre um desafio porque se temos \(k\) variáveis e \(l\) lags, temos \(lk^2+k\) regressores na forma reduzida. Assim estimar um VAR com 8 lags, como sugerido pelo AIC, envolveria 75 parâmetros!

Eu vou estabelecer a seguinte ordem para a decomposição de Chosleki - isso é, para ter uma matriz \(B\) identificada:

• IBC-Br só sofre efeitos defasados
• IPCA só sofre efeitos contemporâneos do IBC-Br
• A taxa Selic é afetada pelo IBC-Br e pela inflação hoje

A escolha acima é mais ou menos ad-hoc, mas é fácil de ser justificada: é mais fácil alterar preços do que a produção, e portanto o IPCA deveria responder mais rápido a choques no produto que o o caminho contrário. E como a decisão da Selic é fixa em muitos meses e o BCB sempre tenta reagir a possíveis oscilações do produto e da inflação sabendo que os efeitos de política monetárias são defasados, faz mais sentido pensar em um BCB que tem previsões quase perfeitas do IPCA e do Produto. Veja que tudo isso são aproximações da realidade, e outros ordenamentos poderiam ser considerados. Veja também que, para a forma reduzida, tanto faz se essa história é verdade ou não: essa história só impacta em como \(B\) deve ser escrito. Veja que eu defini \(\mathbf{x_{t}} = (y_t \phantom{0} \pi_t \phantom{0} i_t)^{\prime}\), e logo essa ordenação implica um B triangular:

\[Bx_t = \begin{pmatrix} 1 & 0 & 0 \\ b_{21} & 1 & 0\\ b_{31} & b_{32} & 1\\ \end{pmatrix} \begin{pmatrix} y_t\\ \pi_t \\ i_t \\ \end{pmatrix} \]

Assim, vamos poder fazer regressões do IBC em duas defasagens do próprio IBC, da inflação e da Selic; regressão do IPCA no IBC do mesmo período, em duas defasagens do IBC, da inflação e da Selic; e regressão da Selic no IPCA e em duas defasagens do IBC, da inflação e da Selic:

eq1 <- dynlm(dibc ~ L(dibc,1:2) + L(ipca,1:2) + L(selic,1:2))
eq2 <- dynlm(ipca ~ dibc + L(dibc,1:2) + L(ipca,1:2) + L(selic,1:2))
eq3 <- dynlm(selic ~ dibc + ipca + L(dibc,1:2) + L(ipca,1:2) + L(selic,1:2))

Vamos rearrumar os coeficientes que saem dessas regressões para formar as matrizes \(A\) e \(B\) e obter \(C\) dai:

B <- diag(1,ncol = 6, nrow = 6)
B[2,1] <- -coef(eq2)[2]
B[3,1:2] <- -coef(eq3)[2:3]

A <- matrix(0, ncol = 6, nrow = 6)
A[4,1] <- 1
A[5,2] <- 1
A[6,3] <- 1
A[1,c(1,4,2,5,3,6)] <- coef(eq1)[2:7]
A[2,c(1,4,2,5,3,6)] <- coef(eq2)[3:8]
A[3,c(1,4,2,5,3,6)] <- coef(eq3)[4:9]

C <- solve(B)%*%A

Veja que podemos usar o pacote vars para checar se Cestá certa, através do comando VAR, que estima a forma reduzida de um VAR. Eu faço isso no código desse post, mas não aqui no blog. Eu também vou criar uma matriz com o desvio padrão do choque na diagonal principal. Assim, a nossa FRI vai dar um choque do tamanho “usual” na economia. Essa será a matriz sd_C:

sd_c <- matrix(0,ncol = 6,nrow=6)
diag(sd_c) <- c(sd(resid(eq1)),sd(resid(eq2)),sd(resid(eq3)),0,0,0)

Com as matrizes \(B\) e \(C\) em mãos, podemos criar duas funções para obter a FRI: a primeira vai obter a resposta ao impulso em um determinado período. A outra vai iterar essa primeira função um número de vezes e guardar cada matriz de resposta ao impulso em um array uma generalização de matrizes para mais de duas dimensões (nosso array vai ter 3 dimensões, a terceira sendo o tempo):

fri_em_t <- function(C,B,h){
  require(expm)
  return((C%^%h)%*%B)
}

fri <- function(C,B,t_max){
  FRI <- array(0,dim=c(nrow(C),ncol(C),(t_max+1)))
  for(j in 1:(t_max+1)){
    FRI[,,j] <- fri_em_t(C,B,(j-1))
  }
  return(FRI)
}

Vamos usar essas funções para obter a resposta a impulso do sistema dez período a frente, e vamos regularizar para que os choques tenham o tamanho médio dos choques da economia:

resposta <- fri(C,solve(B),10)
for(i in 1:dim(resposta)[3]){
  resposta[,,i] <- resposta[,,i]%*%sd_c
}

Em particular, eu estou interessado na resposta a impulso de choques na Selic sobre a inflação. Isso corresponde a posição [2,3] na matriz de resposta ao impulso do período t. Eu coloco, por conveniência, a linha vermelha onde é o zero:

plot(0:10,resposta[2,3,1:11], type = "l", main = "Resposta ao Impulso", sub = "Impulso sobre a Selic na Inflação", xlab = "t", ylab = "")
lines(0:10,rep(0,11),col=2)
grid(col = "grey")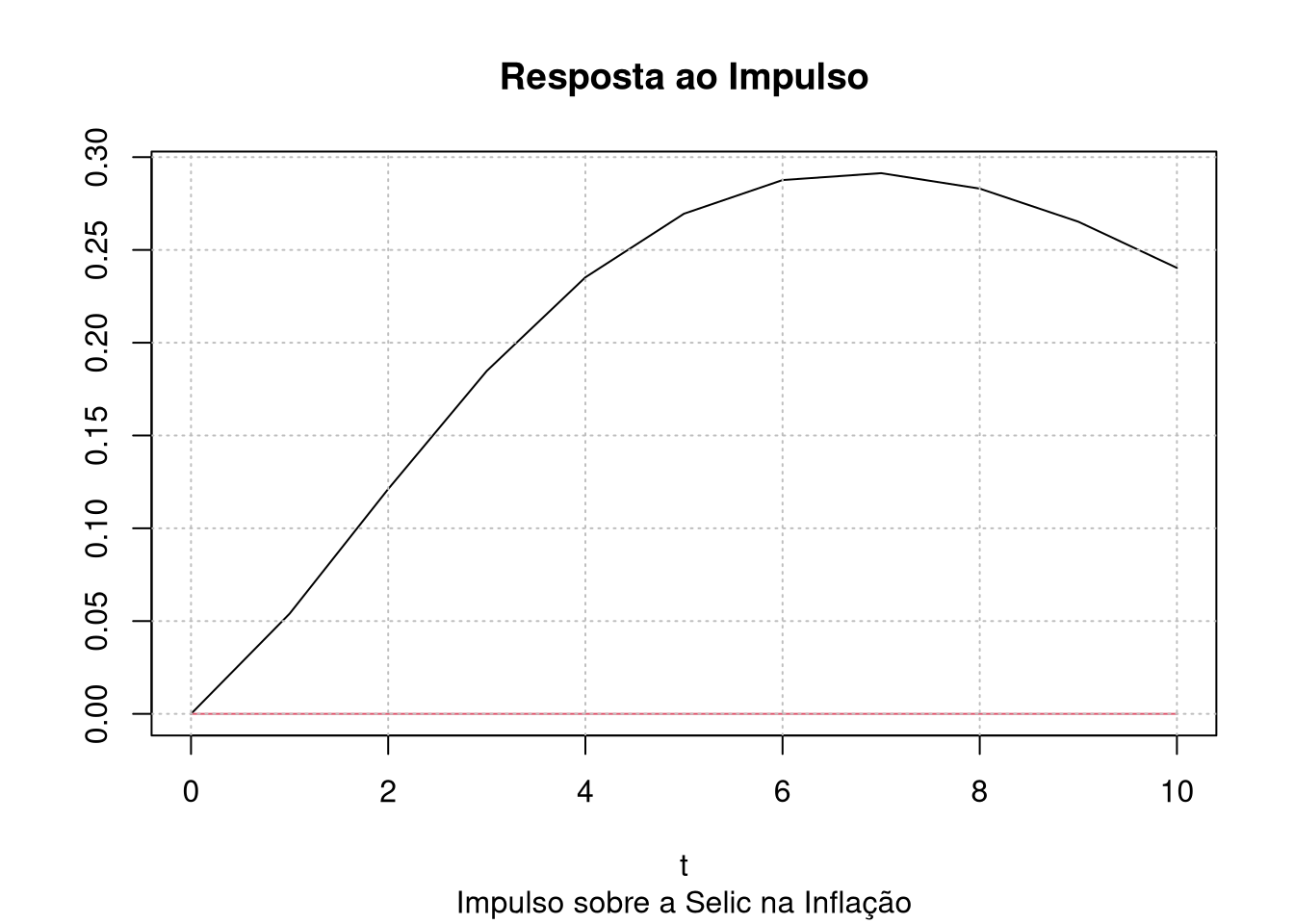

Ou seja, segundo o nosso VAR, um aumento na selic aumenta a inflação. Por que isso? Algo está realmente errado com o nosso VAR? Ou o Brasil é realmente inexplicável? Ou, ainda pior, será que passamos este tempo todo entendo a economia errado?

A boa notícia é que este fenômeno é bem conhecido na literatura de VAR, e recebe o nome de price puzzle. Balke e Emery (1994) tem um gráfico muitissimo parecido com o nosso, para dados dos EUA:

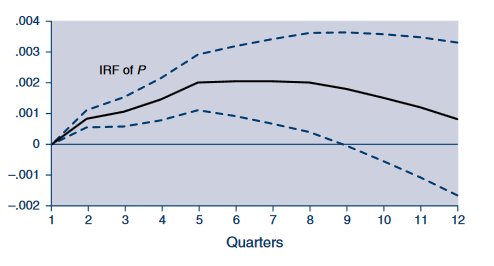
Logo, o problema não está no nosso VAR nem no Brasil. No próximo post eu trarei uma solução

##Escrevendo um VAR(p) como um VAR(1)

Peguemos um VAR qualquer:

\[\mathbf{x_{t}} = C_1 \mathbf{x_{t-1}} + C_2 \mathbf{x_{t-2}} + ... + C_p\mathbf{x_{t-p}}+ \mathbf{u_t}\]

Vamos definir \(\mathbf{z_t} = (\mathbf{x_t} \phantom{0} \mathbf{x_{t-1}} \phantom{0} \mathbf{x_{t-2}} \cdots)^{'}\) Podemos criar uma matriz C que é uma salsicha esperta das matrizes \(C_1, C_2,...\):

\[C = \begin{pmatrix} C_1 & C_2 & \cdots & C_{p-1} &C_p\\ I & 0 & \cdots & 0 & 0\\ 0 & I & \cdots & 0 &0\\ \vdots & \vdots& \ddots & \vdots & \vdots\\ 0 & 0 & \cdots & I & 0\\ \end{pmatrix}\]

Suponha, para facilitar a vida, que \(\mathbf{x_t} = (y_{1t} \phantom{0} y_{2t})'\), e que temos um VAR(2). Nesse caso, \(\mathbf{z_t} = (y_{1t} \phantom{0} y_{2t} \phantom{0}y_{1(t-1)} \phantom{0} y_{2(t-1)})'\)