Prog Dinâmica IIA

Em um post anterior, eu falei sobre a ideia básica de programação dinâmica, e como usamos ela para resolver problemas de otimização no tempo. Naquele post, eu tratei o caso sem incerteza. Este post vai tratar do caso com incerteza.

Vamos mudar um pouco o cenário: o nosso agente continua a maximizar a utilidade, mas dessa vez ele pode investir em um ativo que paga uma taxa de juros \(r\). A incerteza vem do salário dele, que passa a ser uma variável aleatória. A nossa variável de estado é \(W\), a riqueza do indivíduo; e a variável de controle é \(c\), o consumo do indivíduo. Escrevendo no formato usando a função valor, o nosso problema para o período \(t\) é:

\[V_t(W_t,c_t) = U(c_t) + \beta E(V_{t+1}(W_{t+1},c_{t+1})) \text{ sujeito a } W_{t+1} = (1+r)(W_t + \omega_t - c_t)\]

Onde \(U()\) representa a função utilidade e \(\omega_t\) o salário em t - que é uma variável aleatória. Veja que o problema aqui é muito similar ao problema do post anterior, só que agora temos um operador esperança na função valor. Poderiamos tentar calcular a esperança analiticamente, mas isso não é sempre possível. Nós vamos contornar isso simplesmente sorteando alguns valores da distribuição de \(\omega_t\) e tirando a média da função valor para estes sorteios. Veja que o nosso grid, dessa vez, vai ser para a riqueza e não para o salário. O código em Julia que faz isso:

using Plots
using Interpolations
using Optim
using Distributions

r = 0.02
bet = 1/(1+r)

u(c) = log(c)

d = Gamma(1,2)

sal = rand(d,500)

W = range(0.1,stop = 50 , length = 900)
V = Array{Float64}(undef,60,900)

V[1,:] = log.(W)

C = Array{Float64}(undef,60,900)

for t = 1:59
    fun_v = LinearInterpolation(W,V[t,:], extrapolation_bc = Line())
    for i = 1:900
        obj(c) = -u(c) - bet*1/500*sum(fun_v.(W[i] .+ sal .- c))
        sol = optimize(obj,0,W[i])
        V[t+1,i] = - Optim.minimum(sol)
        C[t+1,i] = Optim.minimizer(sol)
    end
end

Ele é muito similar ao código do post anterior. Observe que eu estabeleci a taxa de desconto do agente de maneira a ser “consistente” com a taxa de juros: um \(\beta\) muito maior que o estabelecido deixaria o agente excessivamente paciente; um \(\beta\) muito menor que o estabelecido deixaria o agente sem poupar nunca. Eu escolhi a distribuição Gama para a distribuição do salário porque é uma distribuição que tem suporte nos valores positivos - um salário negativo não faz sentido. Vamos supor que o agente começa sem nenhuma riqueza, só o salário. Vamos construir uma possível trajetória do agente:

start_val = 0

wealth = Array{Float64}(undef,60)
wealth[60] = start_val + sal[60]
consu = zeros(60)

for t = 60:-1:2
    c_func = LinearInterpolation(W,C[t,:],extrapolation_bc = Line())
    consu[t] = c_func(wealth[t]+sal[t])
    wealth[t-1] = (1+r)*(wealth[t] + sal[t] - consu[t])
end

consu[1] = wealth[1]

plot(consu[60:-1:1], lab="Consumo", legend= :topleft )
plot!(wealth[60:-1:1], lab = "Riqueza")
plot!(sal[60:-1:1], lab = "Salário")

Vamos ver a trajetória do consumo e da riqueza do agente:

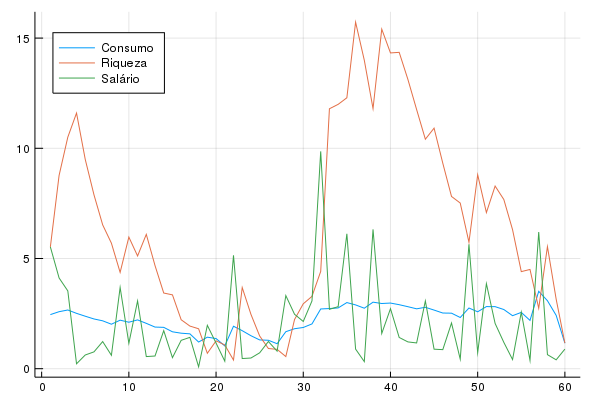
Isso ilustra a ideia de ciclo de vida e suavização do consumo, que em Macroeconomia são associados a Franco Modigliani e Milton Friedman: o agente não consome só uma fração da renda dele hoje, mas sim uma fração da renda dele ao longo do tempo. Veja que a riqueza varia muito mais que o consumo: em períodos em que o agente está rico, ele poupa; e em períodos de vacas magras ele consome a riqueza.

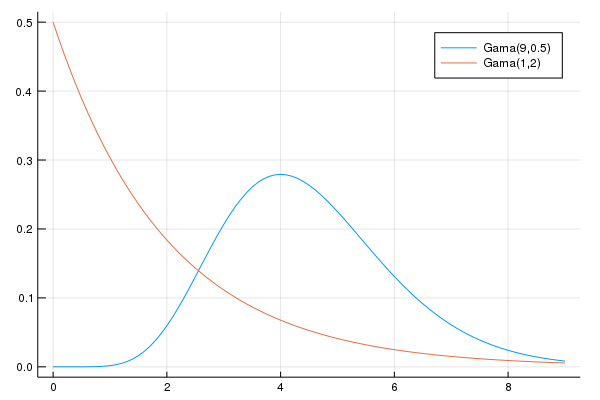
Veja que nesse primeiro caso, usamos uma distribuição Gama(1,2). O que acontece se mudarmos os parâmetros da distribuição? A distribuição Gama é bastante versátil, e mudanças nos parâmetros geram mudanças profundas no formato da distribuição, como a imagem acima sugere.

Vamos repetir o exercício, mas usando a Gama(9,0.5). Nesse caso, temos o mesmo código que acima, mas mudamos a variável d, que estabelece a distribuição, para a nova distribuição. Veja que isso exige reestimar as funções, já que mudamos a distribuição. A nova trajetória tem a seguinte aparência:

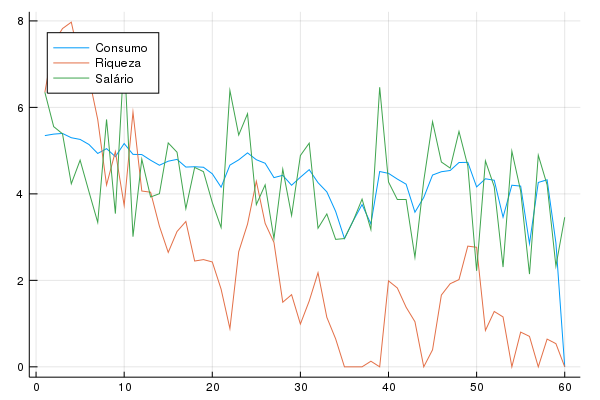
Veja que o consumo varia bem mais nesse caso, mas ainda assim a riqueza varia ainda mais. Esse caso também deixa claro que, mais para o fim da vida, o consumo flutua muito. A intuição por trás é que teremos menos períodos a frente para suavizar o consumo, e logo menos oportunidades de ganhar dinheiro e consumir.

Veja que em todos esses casos, a distribuição dos salários é independente ao longo do tempo. Isso não é, necessariamente, uma boa aproximação da realidade. O problema é que, sair do mundo de variáveis independentemente distribuídas complica tudo.

Uma maneira de facilitar o problema e permitir alguma dependência temporal é usando cadeias de Markov finitas. Uma cadeia de Markov é um processo estocástico que só depende da realização anterior - por exemplo, um AR(1). No caso, ela é finita se temos um número finito de estados possíveis. Neste post eu já usei cadeias de Markov. A transição entre estados é governado por uma matriz, onde cada linha representa a probabilidade de sair do estado linha e ir para o estado coluna. Vamos supor que temos apenas 2 estados e a matriz de transição é a seguinte:

\[\begin{pmatrix} 0.5 & 0.5\\ 0.4 & 0.6\\ \end{pmatrix}\]

Então, a probabilidade de permanecer no estado 1 é de 0.5; e a probabilidade de migrar para o estado 2, condicional a estar no estado 1, é de 0.5. Vamos estabelecer que o valor do salário em cada estado é (1,2). Nesse caso, podemos calcular o valor esperado analiticamente, simplesmente fazendo \(\displaystyle \sum P(x_j|x_i)V(x_j)\) quando estivermos no estado x_i.

O código abaixo estima o consumo no caso em que o salário segue uma cadeia de Markov com apenas dois estados. Veja que isso exige mais um for (mas teoricamente poderiamos ter adicionado os estados usando as matrizes direto e cada iteração devolveria uma dupla de valores):

using Plots
using Optim
using Interpolations
using Distributions

Transition_matrix = [[0.5 0.5];[0.4 0.6]]

w = [1 ;2]

u(c) = log(c)

T = 70

r = 0.05
beta = 1/(1+r)

grid = range(0,stop=10,step=0.05)

V = Array{Float64}(undef,T,length(grid),2)
P = Array{Float64}(undef,T,length(grid),2)

V[1,:,1] = u.(grid)
V[1,:,2] = u.(grid)

P[1,:,1] = grid
P[1,:,2] = grid

for i=1:(T-1)
    for k=1:2
        v_func = LinearInterpolation(grid,V[i,:,k], extrapolation_bc = Line())
        for j = 1:length(grid)
            func(c) = -u(c) - beta*Transition_matrix[k,:]'*v_func.(w .+(1+r)*(grid[j]-c))
            otimo = optimize(func,0,grid[j])
            V[i+1,j,k] = -Optim.minimum(otimo)
            P[i+1,j,k] = Optim.minimizer(otimo)
        end
    end
end

start_val = 2
initial_state = 1

cons = Array{Float64}(undef,T)
riqueza = Array{Float64}(undef,T)
riqueza[T] = start_val
state = Array{Int64}(undef,T)
state[1] = initial_state

dist = Uniform(0,1)

for j = 1:(T-1)
    aux = state[j]
    vv = rand(dist,1)
    if(vv <= Transition_matrix[aux,:])
        state[j+1] = 1
    else state[j+1] = 2 end
end

state = state[T:-1:1]

for j = T:-1:2
    cons_foo = LinearInterpolation(grid,P[j,:,state[j]],extrapolation_bc = Line())
    cons[j] = cons_foo(riqueza[j]+w[state[j]])
    riqueza[j-1] = (1+r)*(riqueza[j] + w[state[j]] - cons[j])
end

cons[1] = riqueza[1]

plot(riqueza[T:-1:1], lab = "Riqueza")
plot!(cons[T:-1:1], lab = "Consumo")
scatter!(state[T:-1:1], lab = "Estado")

Veja que só tem duas alterações desse código para o anterior:

• Tem um for a mais na parte de estimar a função consumo, para permitir a depêndencia da probabilidade ao estado em que o agente se encontra.
• Tem um trecho extra no qual computo, a priori, a evolução dos estados. Para sortear qual estado vai seguir, eu preciso saber o estado atual (state[j]) - isso vai separar apenas uma linha da tabela; e sortear um número entre 0 e 1. Se esse número for menor que o valor da primeira entrada, então passamos (ou permanecemos) no estado 1. Caso contrário, pulamos para o estado 2. Por exemplo, se estivermos no estado 1 e sortearmos 0.3, como 0.3 < 0.4, permaneceremos no estado 1. Veja que isso gera exatamente as probabilidades certas de cair em cada estado, já que para a uniforme (0,1), \(P(X \leq x) = x\). Logo, \(P(X \leq 0.4) = 0.4\)

O gráfico desse caso é o seguinte:

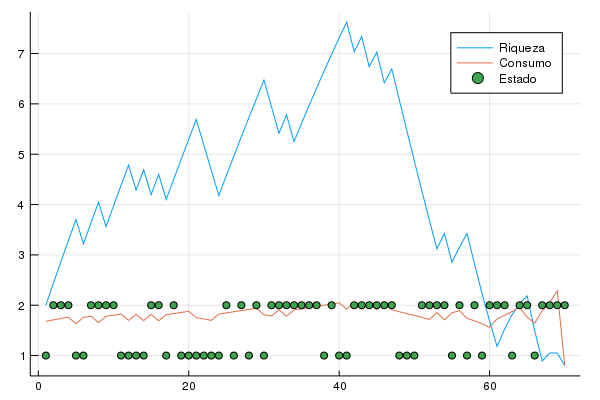
Ou seja, mesmo no caso em que salários seguem um processo com depêndencia ao temporal, a mensagem fundamental permanece: pessoas suavizam o consumo ao longo do tempo.

No outro post eu tratarei de como computar a decisão do consumidor quando ele se depara com um problema com infinitos períodos.