Do domínio temporal para o domínio frequência

Passar um filtro do domínio temporal para o domínio da frequência envolve usar a Transformada de Fourier. A regra de bolso é que trocamos todos os \(B\) por \(e^{-i\omega}\), onde \(\omega\) é a frequência que estamos interessados e \(i = \sqrt{-1}\). Apesar da interpretação de \(\omega\) não ser direta, é fácil relacionar a frequência com o período \(p\), já que \(p=\frac{2\pi}{\omega}\). O período é quanto tempo demora para aquele componente da série se repetir. Elementos são de alta frequência - tem \(\omega\) grande - se repetem em períodos mais curtos, enquanto elementos de baixa frequência demoram mais a se repetir. São os componentes de baixa frequência que estão associados a tendência da série. Muitas vezes temos o interesse em remover esse componente para obter uma série estacionária. Vou exemplificar isso tudo com o “filtro” de primeira diferença, que pode ser escrito no time domain como \(F(B) = 1 - B\). Vamos usar a regra de bolso e substituir B por \(e^{-i\omega}\) e obtemos a expressão \(1 - e^{-i\omega}\). Veja que isso é um número complexo, e que números complexos aceitam a representação na forma polar (basta pensar que a parte real e a parte imaginária formam um vetor). Então seja um número com parte real \(a\) e parte imaginária \(b\), i.e. \(a+bi\). Ele pode ser reescrito como \(ge^{i\theta}\), onde \(g = \sqrt{a^2+b^2}\) e \(\theta = tan^{-1}(\frac{b}{a})\).

O importante dessa representação é que \(g\) pode ser interpretado como o ganho do filtro para a frequência \(\omega\). Um paralelo seria o equalizador da maior parte dos players de música, que permitem você aumentar o volume da frequências mais baixas (associadas ao baixo e a bateria, por ex.) e das mais altas (voz e guitarra, por ex.)¹. Já \(\frac{\theta}{\omega}\) tem a interpretação de em quantas unidades de tempo o nosso filtro defasa a série (e isso é chamado da fase do filtro).

Uma propriedade conveniente da representação no domínio da frequência é que é fácil saber o que acontece com uma série se passamos por múltiplos filtros: basta multiplicar as representações no domínio da frequência. Então o efeito de passar a séria \(x_t\) pelos filtro \(\alpha(B)\) e \(\beta(B)\) é simplesmente \(\alpha(e^{-iw})\beta(e^{-iw})\). Isso facilita enormemente a vida de analisar o que acontece quando você passa os dados por n filtros.

Alguns Exemplos

Um filtro óbvio é o filtro defasar uma vez. Ele não deveria dar ganho nenhum a série (espera-se) e ter fase que reflita a defasagem por um período. Vamos escrever isso como uma função no R, usando a nossa regra de trocar B por \(e^{-i\omega}\):

backshift <- function(w){exp(-1i*w)}

x <- seq(0,pi,by = 0.05)

plot(x,Mod(backshift(x)),type="l",ylab = " ", xlab = "Frequência", main = "Ganho do Filtro de Defasar uma vez")
grid(col = "darkgrey")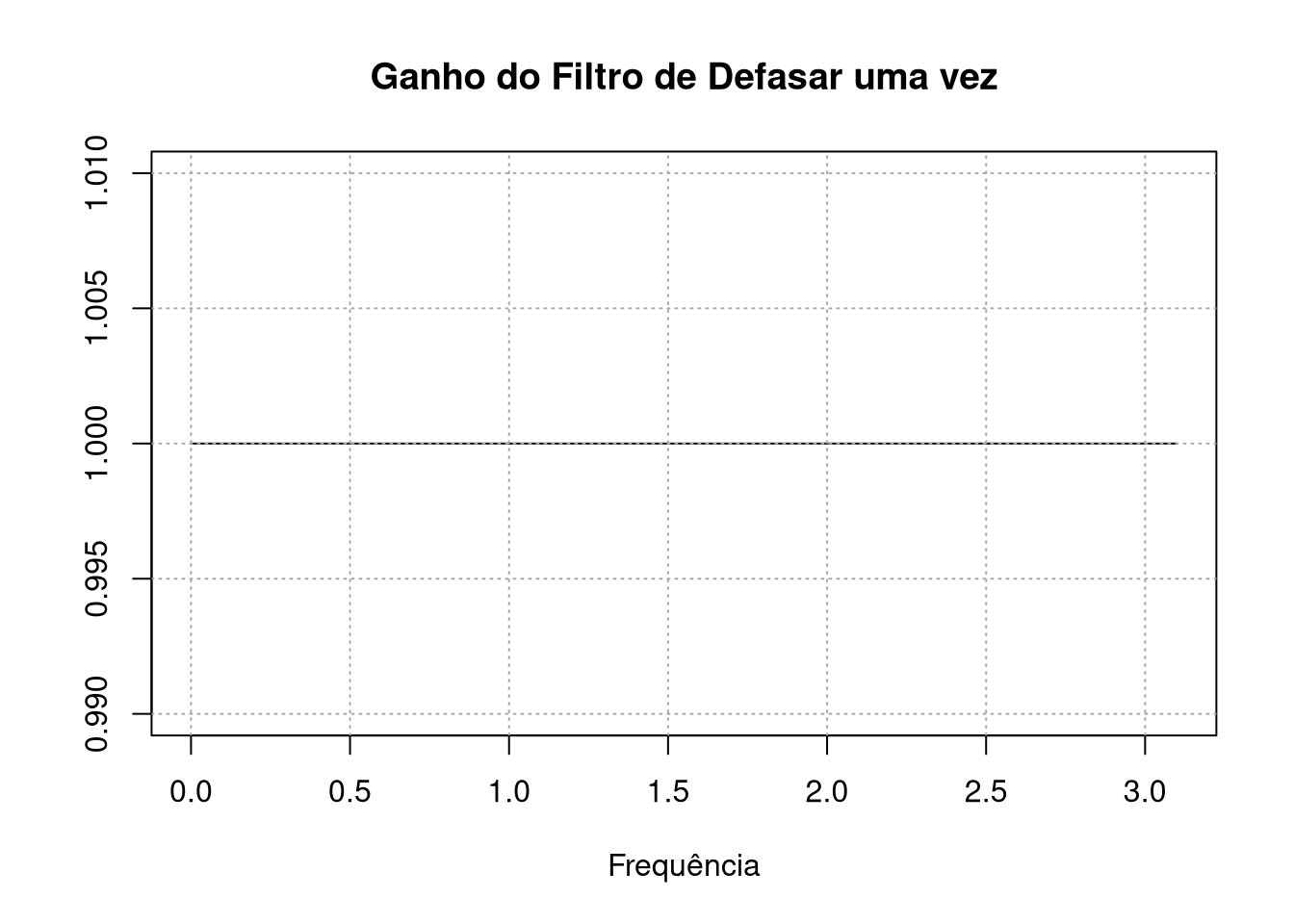

plot(x,Arg(backshift(x))/x,type="l",ylab = " ", xlab = "Frequência", main = "Fase do Filtro Defasar uma vez")
grid(col = "darkgrey")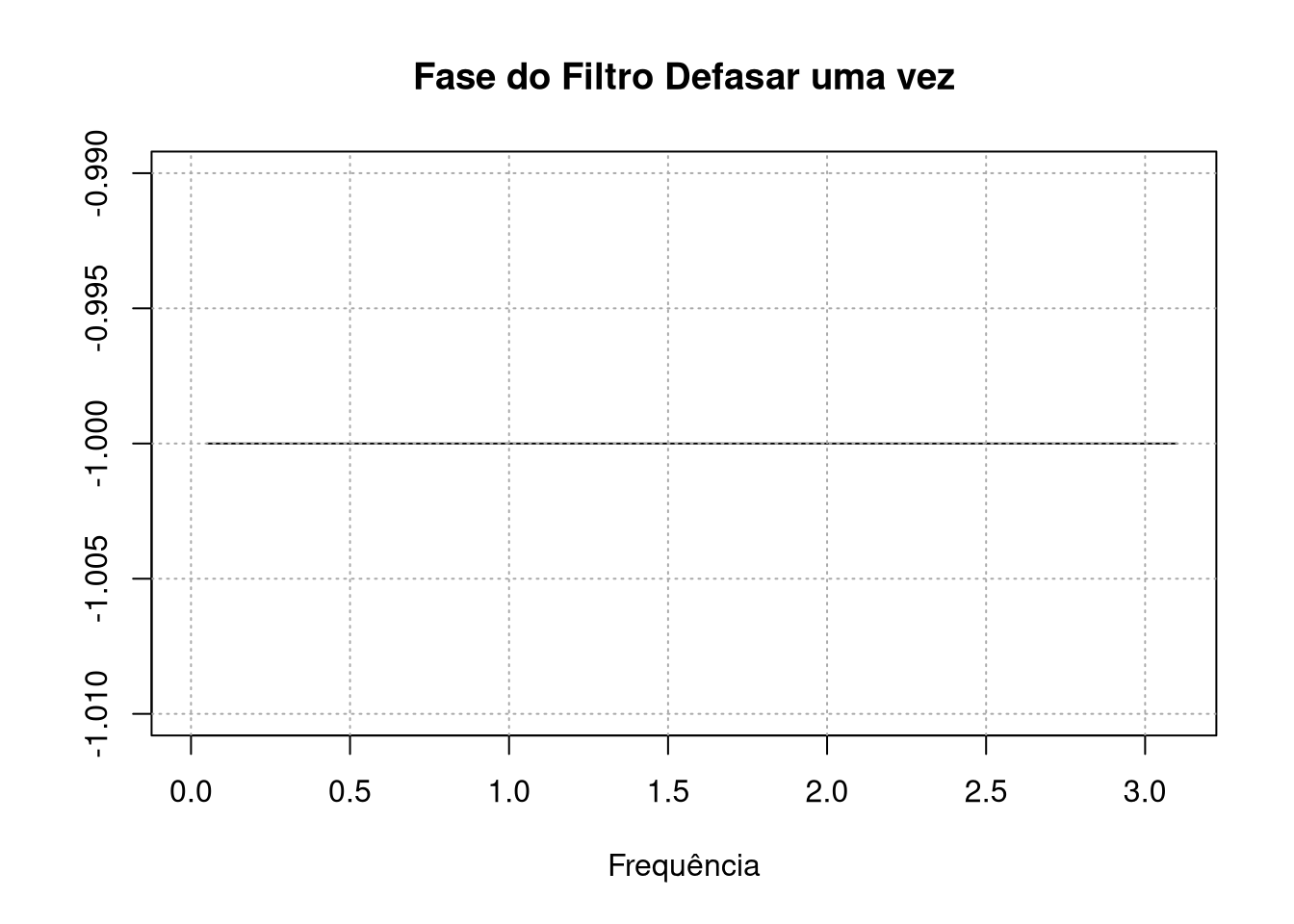

Para nosso grande alívio (e nenhuma surpresa) defasar uma vez a série não gera ganho em nenhuma frequência e altera todas as frequências uma unidade de tempo para trás. Vamos ver o ganho do filtro de primeira diferença:

fd <- function(w){
  1-exp(-1i*w)
}

x <- seq(0,pi,by = 0.05)

plot(x,Mod(fd(x)),type="l",ylab = " ", xlab = "Frequência", main = "Ganho do Filtro de Primeira Diferenças")
grid(col = "darkgrey")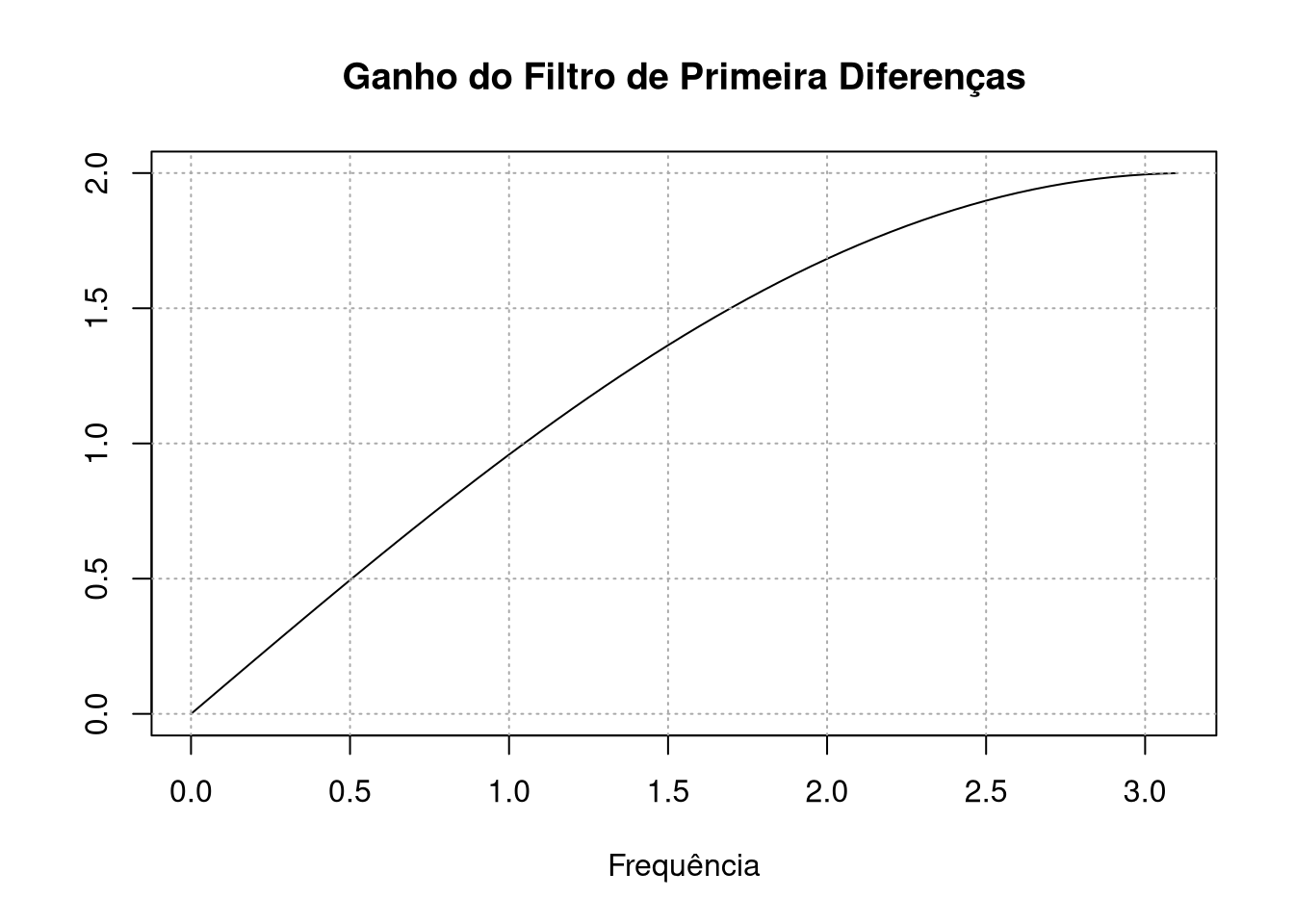

plot(x,Arg(fd(x))/x,type="l",ylab = " ", xlab = "Frequência", main = "Fase do Filtro de Primeira Diferenças")
grid(col = "darkgrey")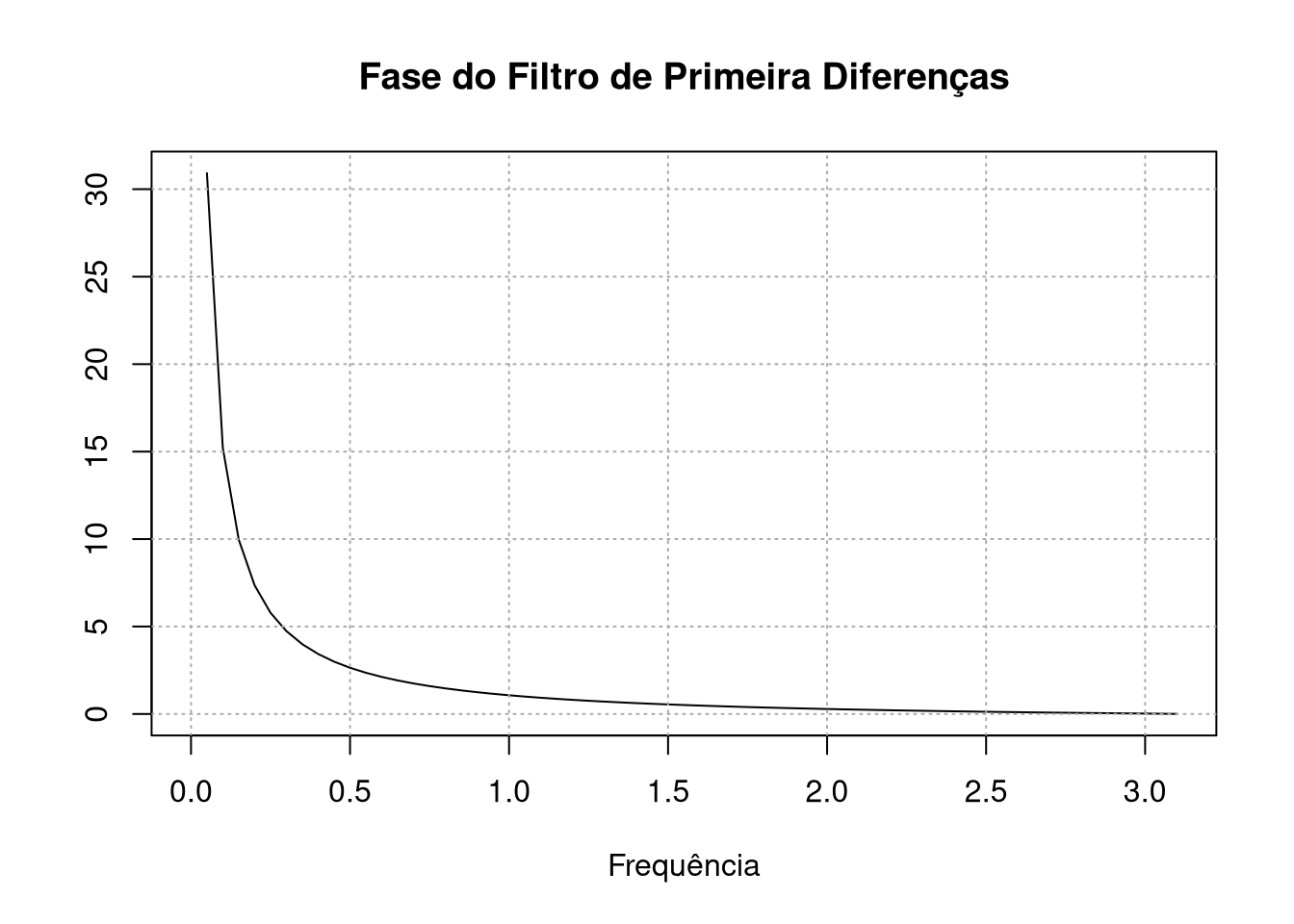

Como prometido, as frequências mais baixas tem ganho próximo a zero, o que tem como efeito sumir com a tendência da série. A fase dele tem um comportamento esquisito nas frequências mais baixas - justamente as que são atenuadas - mas para frequências mais altas ele decai para 0 - logo, não altera em nada a fase. Vamos aos exemplos mais interessantes: que tal uma média móvel que troca o valor de hoje pela média entre o valor dele e dos seus dois valores anteriores e dois valores posteriores? Isso pode ser escrito, no domínio temporal, como:

\[MA(L) = \frac{1}{5}\left(L + L^2 + 1 + L^{-1} + L^{-2} \right)\]

Esse é um bom momento para apresentar o conceito de filtro simétrico : um filtro é dito _simétrico se \(a_j = a_{-j}\) (Lembrando que o filtro é definido como \(\displaystyle \sum_{j=-\infty}^{\infty} a_j B^{j}\)). Veja que esse é o caso. Como \(e^{-ix} + e^{ix} = 2cos(x)\), então o filtro pode ser reescrito na representação espectral como \(a_0 + 2\sum_{j=1}^\infty a_j \cos(jw)\). Veja que não temos nenhum número imaginário, então um filtro simétrico não induz nenhuma mudnça de fase, e podemos só olhar o ganho dele. Vamos implementar o filtro MA no R usando a nossa regra de bolso e olhar para os ganhos que o filtro gera:

ma_freq_domain <- function(w){
  1/5*(exp(-1i*w) + exp(-2i*w)+ 1 + exp(1i*w) + exp(2i*w)) 
}

x <- seq(0,pi,by = 0.05)

plot(x,Mod(ma_freq_domain(x)),type="l",ylab = " ", xlab = "Frequência", main = "Ganho do Filtro MA")
grid(col = "darkgrey")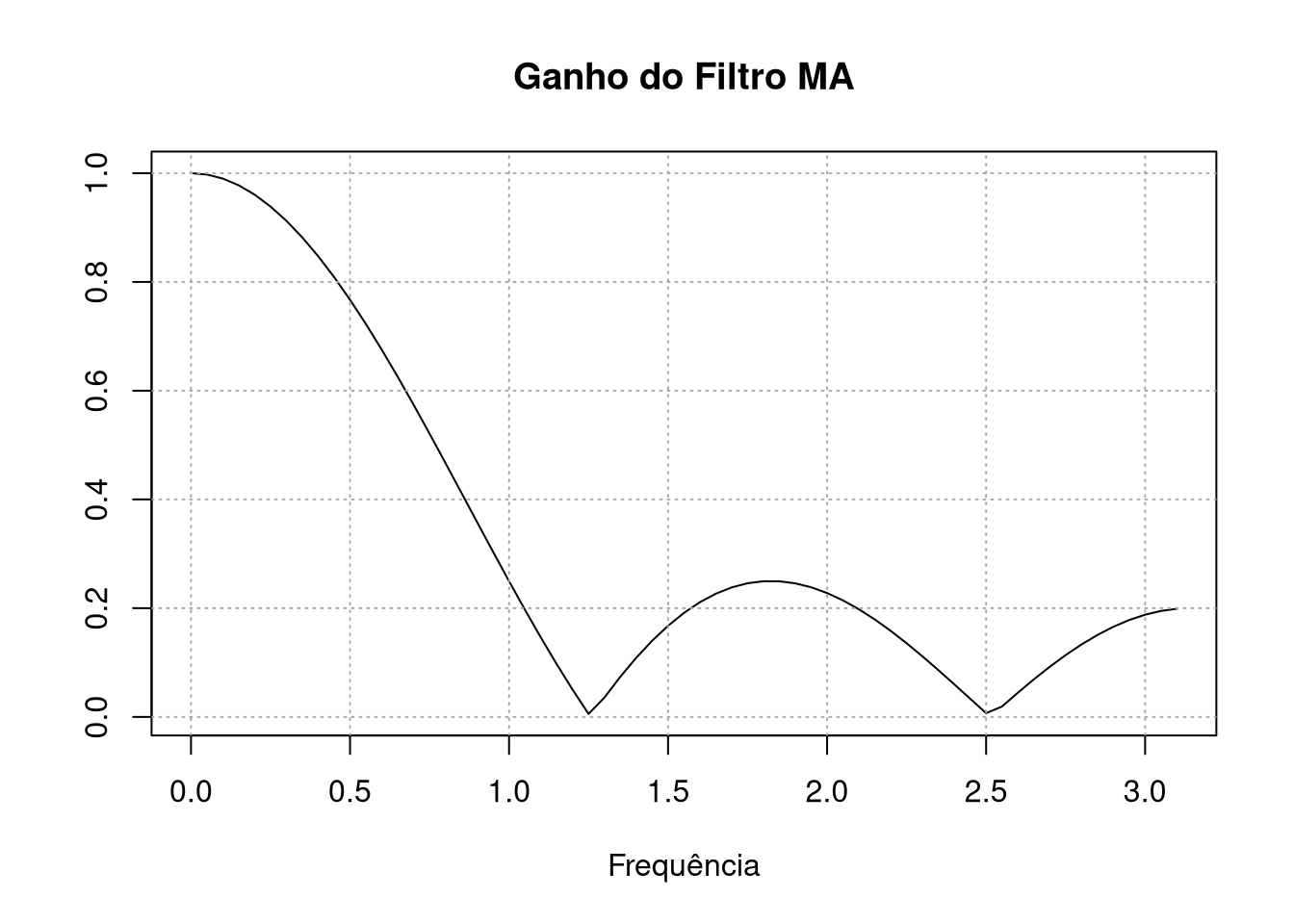

O que acontece se usarmos o filtro MA acima para tirar a tendência de uma série? Basta analisar o ganho de 1 - MA:

ma_detrender <- function(w){1-ma_freq_domain(w)}

plot(x,Mod(ma_detrender(x)),type="l",ylab = " ", xlab = "Frequência", main = "Ganho do Filtro MA")
grid(col = "darkgrey")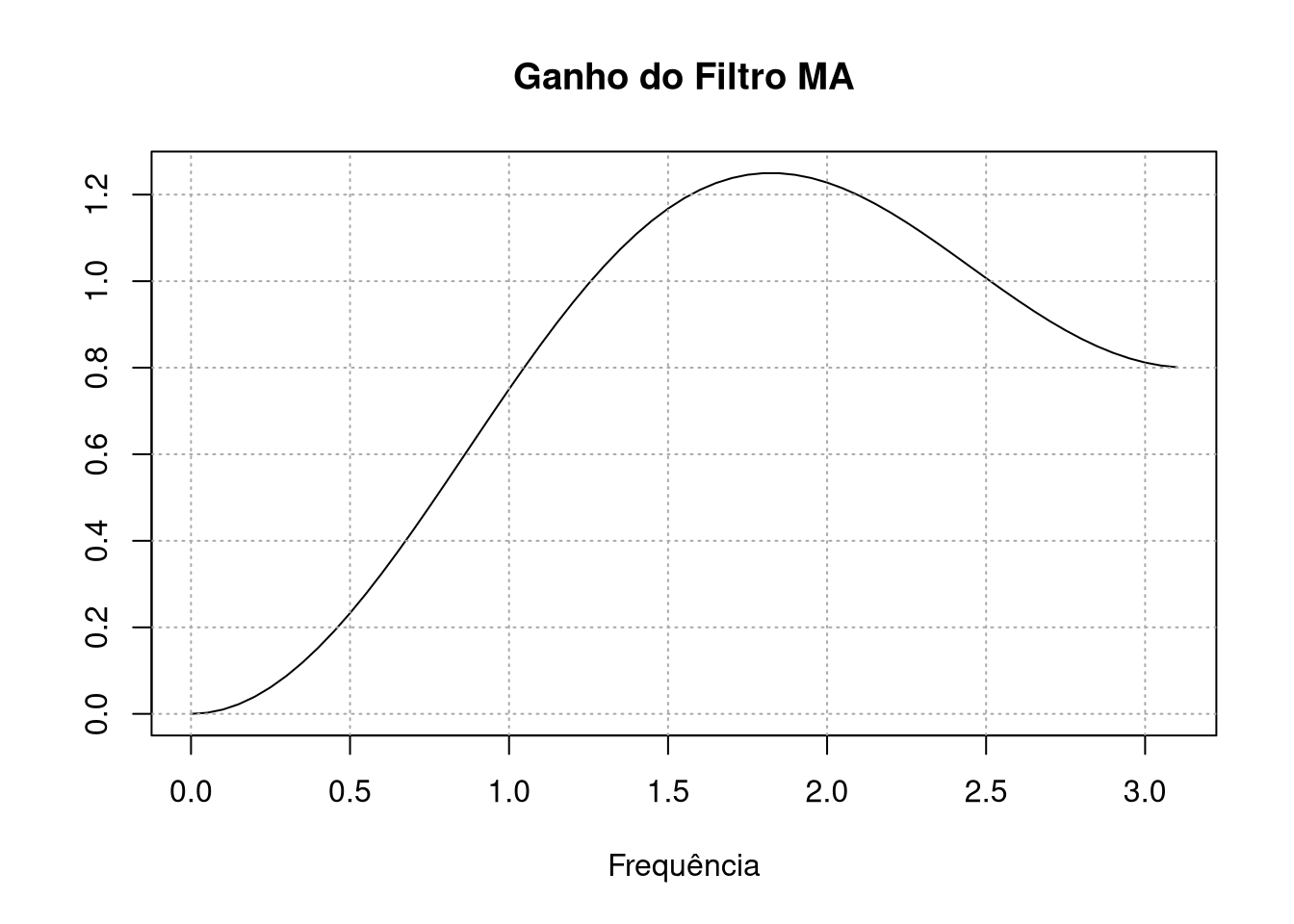  

Veja que para frequências entre 1,5 e 2 (que correspondem a períodos de 3 a 4 trimestres para dados trimestrais), o ganho do filtro é maior que 1. Logo, os dados que passarem por este filtro vão ter essa frequência realçada. Isso gera um problema perigoso: dizer que os dados exibem um determinado padrão porque você passou ele num filtro que gera este padrão. É importante entender o que cada filtro que você passa nos dados faz para evitar apontar padrões nos dados que foram gerados pelos filtros.

Em um exemplo mais interessante, vamos analisar o filtro HP. King e Rebbelo (1993) obtém o ganho do filtro a partir das condições de primeira ordem do filtro. O ganho é:

\[\frac{4\lambda(1-\cos(\omega))^2}{1+4\lambda(1-\cos(\omega))^2}\]

Gain_HP <- function(w,lam){
  4*lam*(1-cos(w))^2/(1+4*lam*(1-cos(w))^2)
}

plot(x,Gain_HP(x,1600), main = "Ganho filtro HP, \u03bb = 1600", type = "l", ylab = "Ganho",xlab="Frequência")
grid(col = "darkgrey")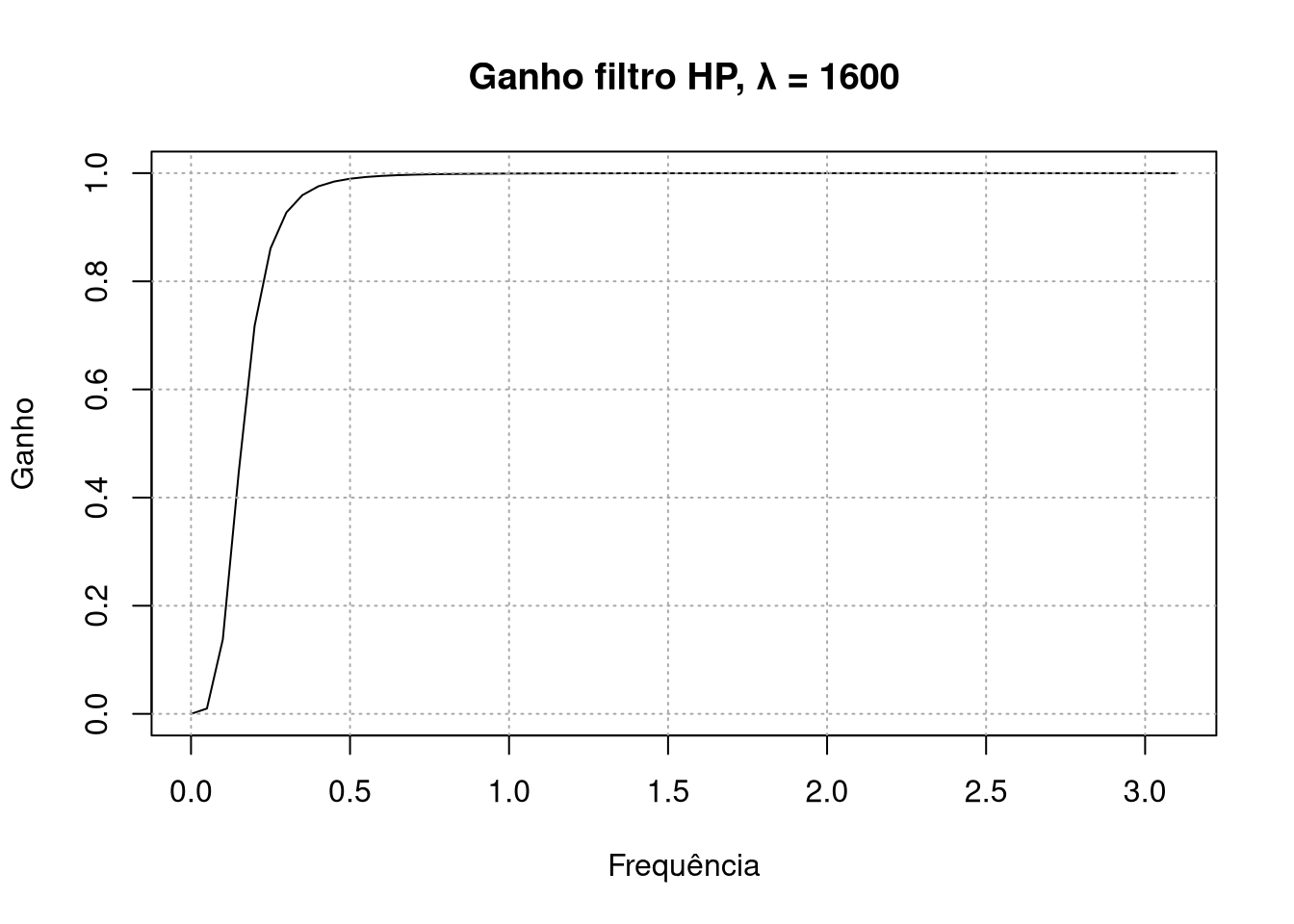

Como esperado, o filtro HP remove a frequência mais baixa e mantém as frequências mais altas, ou seja, remove a tendência. Veja que isso permite com que a frequência associada a sazonalidade passe pelo filtro, então apesar de retirar a tendência o filtro HP não retira sazonalidade.

Espero que este post ajude a entender como analisar filtros, que são frequentemente utilizados para analisar séries temporais. Futuramente, irei apresentar outros filtros com propriedades interessantes.

Referências

King, Robert G., and Sergio T. Rebelo. 1993. “Low frequency filtering and real business cycles.” Journal of Economic Dynamics and Control. doi:10.1016/S0165-1889(06)80010-2.