Comportamento de Random Walks
Um processo estocástico autoregressivo com \(1\) lag, doravante chamado de AR1, é, no caso simplificado em uma dimensão que eu abordarei aqui, descrito como:
\[y_t = \beta y_{t-1} + \mu_t\] Para algum \(y_o = c\) e, no caso com que lidaremos hoje, \(\beta \in \mathbb{R}\) e \(\mu_t \sim N(0, \sigma^2)\), logo vale que $[_t] = 0 $.
Variância e Esperança do Processo AR1
Esperança
Vamos agora caracterizar o Valor Esperado e a Variância desse processo, assim como caracterizaríamos os dois primeiros momentos centrais de uma distribuição. Note que o operador de Esperança é linear, isso é importante.
\[\mathbb{E} [y_t] = \mathbb{E} [\beta y_{t-1} + \mu_t]\] \[\mathbb{E} [y_t] = \beta\mathbb{E} [ y_{t-1}] + \mathbb{E}[\mu_t]\] \[\mathbb{E} [y_t] = \beta\mathbb{E} [ \beta y_{t-2} + \mu_{t-1}] + 0\] \[\mathbb{E} [y_t] = \beta^2\mathbb{E} [y_{t-2}] + \mathbb{E}[\mu_{t-1}] + 0\]
Acho que o leitor já captou o padrão aqui. Se não, recomendo continuar o processo mais algumas vezes no papel. No final chegaremos em:
\[\mathbb{E} [y_t] = \beta^t y_0\]
Espero que seja claro ao leitor também - ou que a verificação não tome muito tempo - que se \(| \beta | < 1\) então \(\lim_{t \to \infty}\beta^t y_0 = 0\). No entanto o mesmo limite explode para infinito se o parâmetro for maior ou igual a \(1\) em módulo.
Variância
Note que variância de constantes dadas é \(0\) e que variância de combinações lineares de variáveis aleatórias independentes é soma das variâncias de cada variável. Podemos reduzir a variância de \(y_t\) à:
\[\mathbb{V}[y_t] = \mathbb{V} [\sum_{i=1}^t \mu_i] \] \[ \mathbb{V} [\sum_{i=1}^t \mu_i] = \sum_{i=1}^t\mathbb{V}[\mu_i]\] Como \(\mathbb{V}[\mu_i] = \sigma^2\), vale que \(\mathbb{V}[y_t] = t \sigma^2\). Esperamos variância crescente com o tempo, porém que sorteios diferentes do mesmo processo se cancelem perto de zero - ou melhor, que não exista alguma forte de viés para números positivos ou negativos. Será que podemos verificar isso acontecendo?
Simulando
Vamos simular alguns processos random walk:
library(tidyverse)
library(gganimate)
processos = list()
tmax = 10000
inicial = 0
nprocessos = 50
beta = 1
set.seed(1234)
for(i in 1:nprocessos) {
t = seq(1, tmax)
processo = vector(length = tmax)
processo[1] = inicial
for(j in 2:tmax) {
choque = rnorm(n = 1)
processo[j] = beta*processo[j-1] + choque
}
dados = tibble(t = t,
processo = processo)
processos[[i]] = dados
}
processos = do.call(rbind, processos) # agregamos as listasVamos entender o que acabamos de produzir. Criamos 50 processos estocásticos com características muito similares. Condição inicial no zero, sujeitos a choques com a mesma distribuição probabilística e com a mesma “inércia”. Valores anteriores são repassados integralmente. Vamos primeiro visualizar um processo sozinho:
processos[1:tmax,] %>%
ggplot(aes(x = t, y = processo)) +
geom_point() +
transition_reveal(t)
processos[1:tmax,] %>%
ggplot(aes(x = t, y = processo)) +
geom_line(size = 1.2)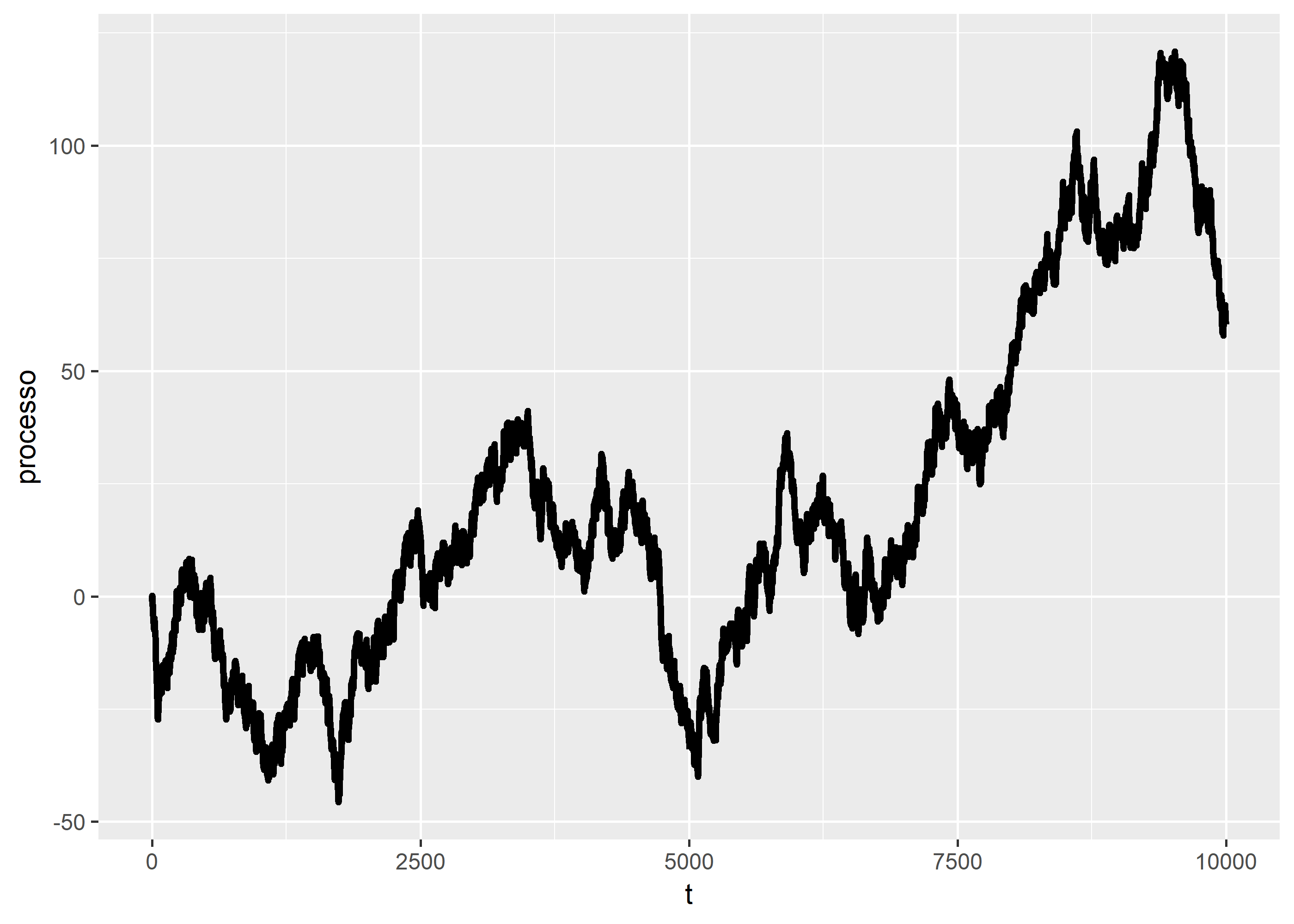
Vamos observar agora o comportamento conjunto dos processos pontualmente em cada instante \(t\).
processos %>%
ggplot(aes(x = t, y = processo)) +
geom_point() +
transition_reveal(t)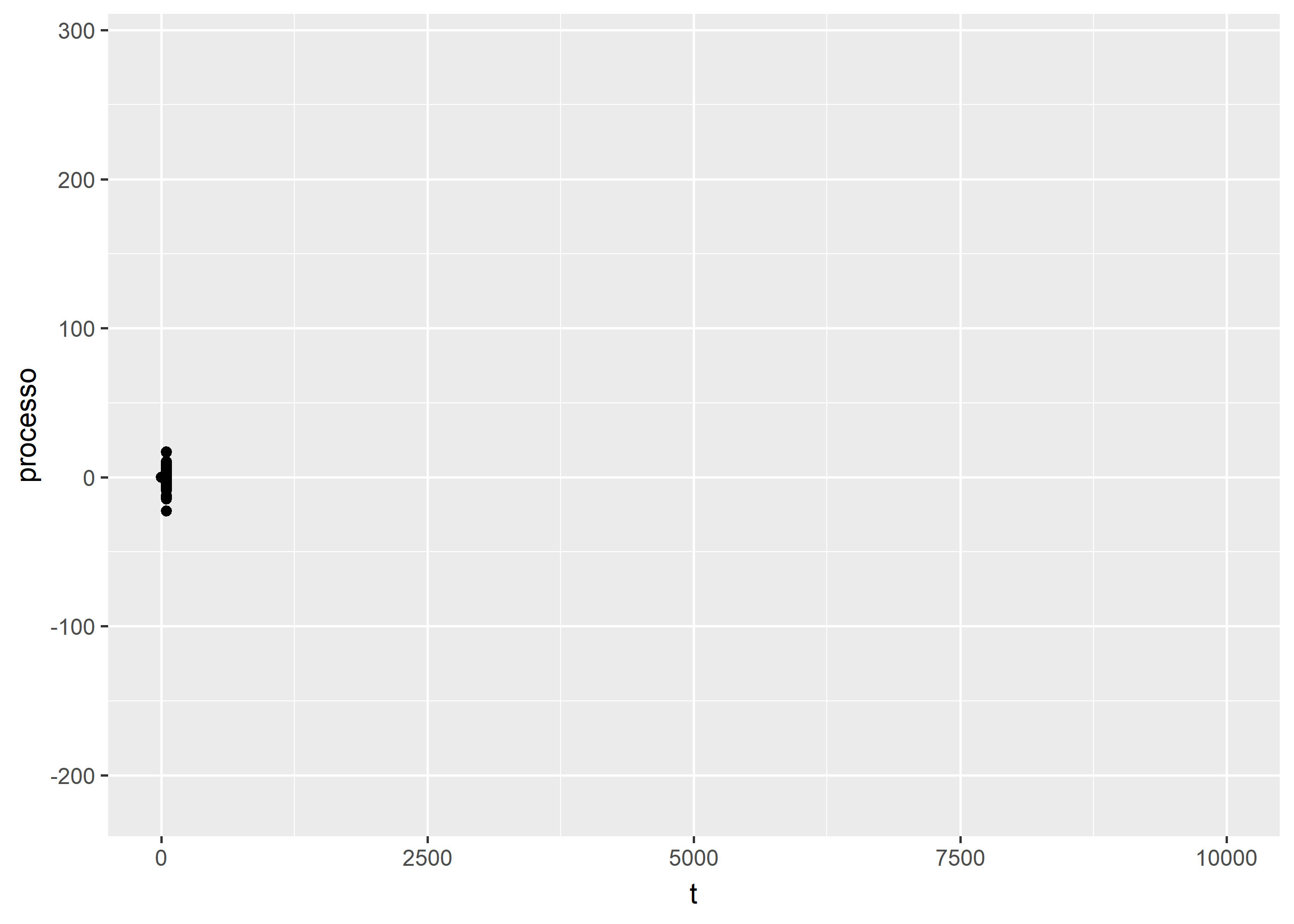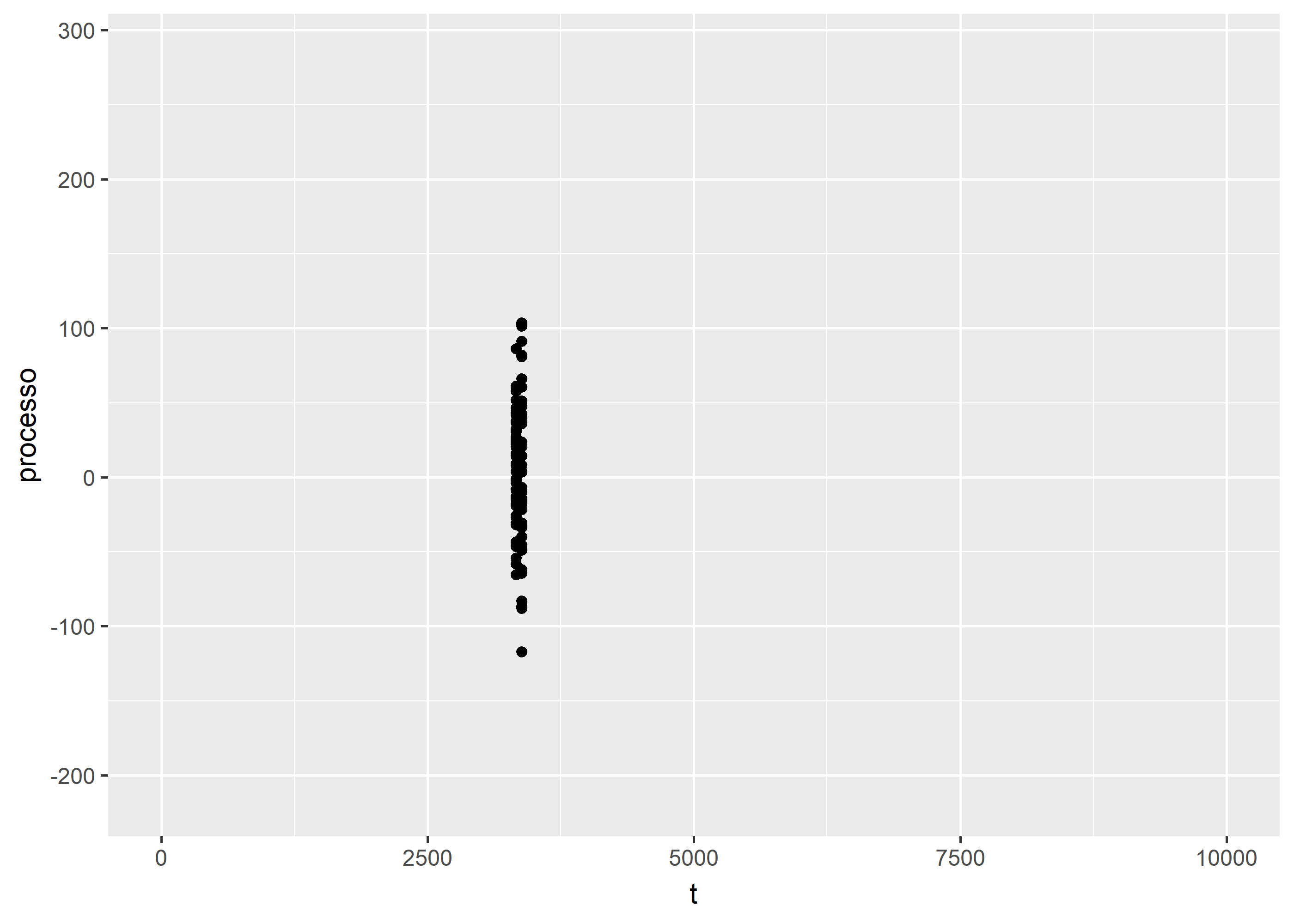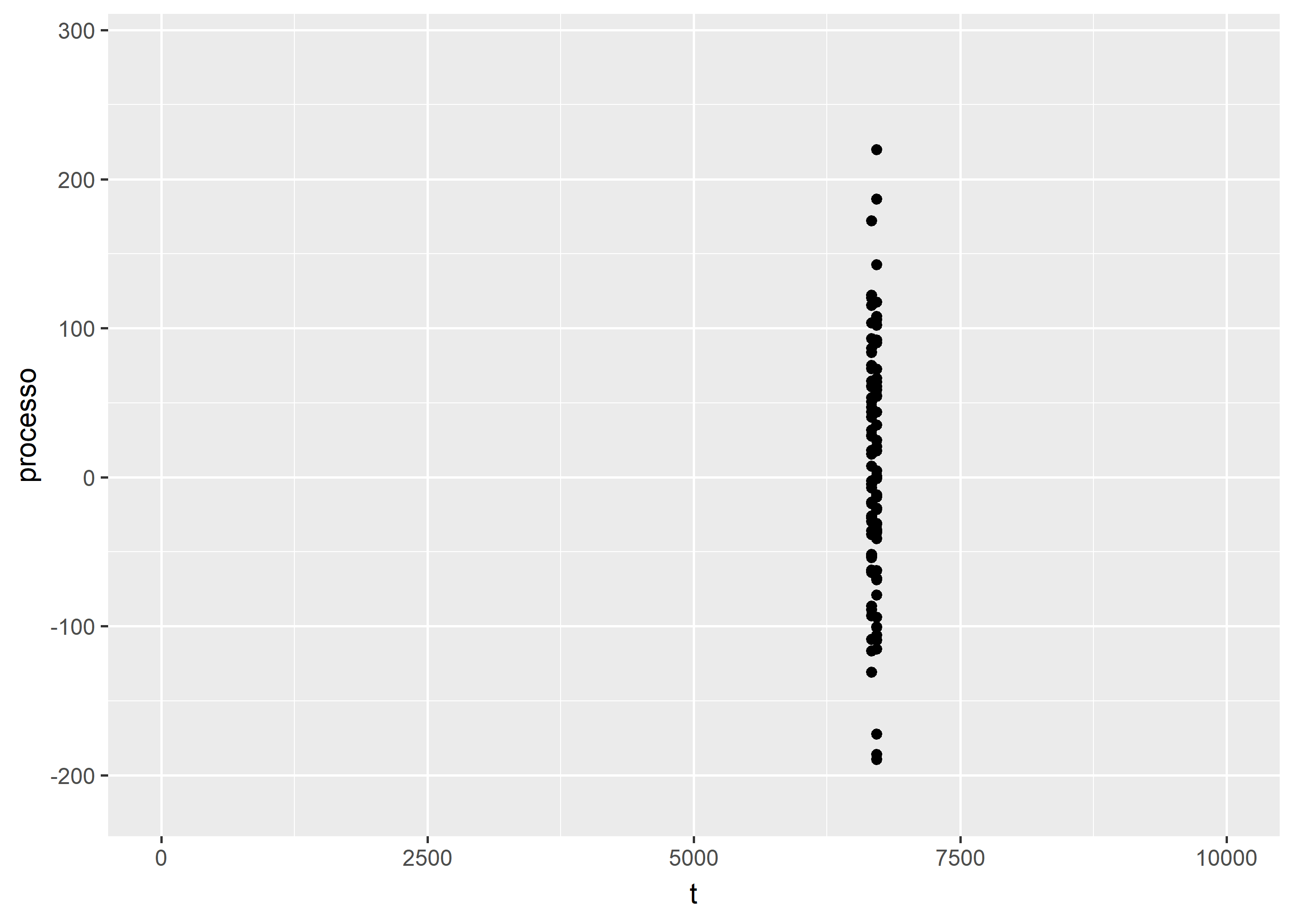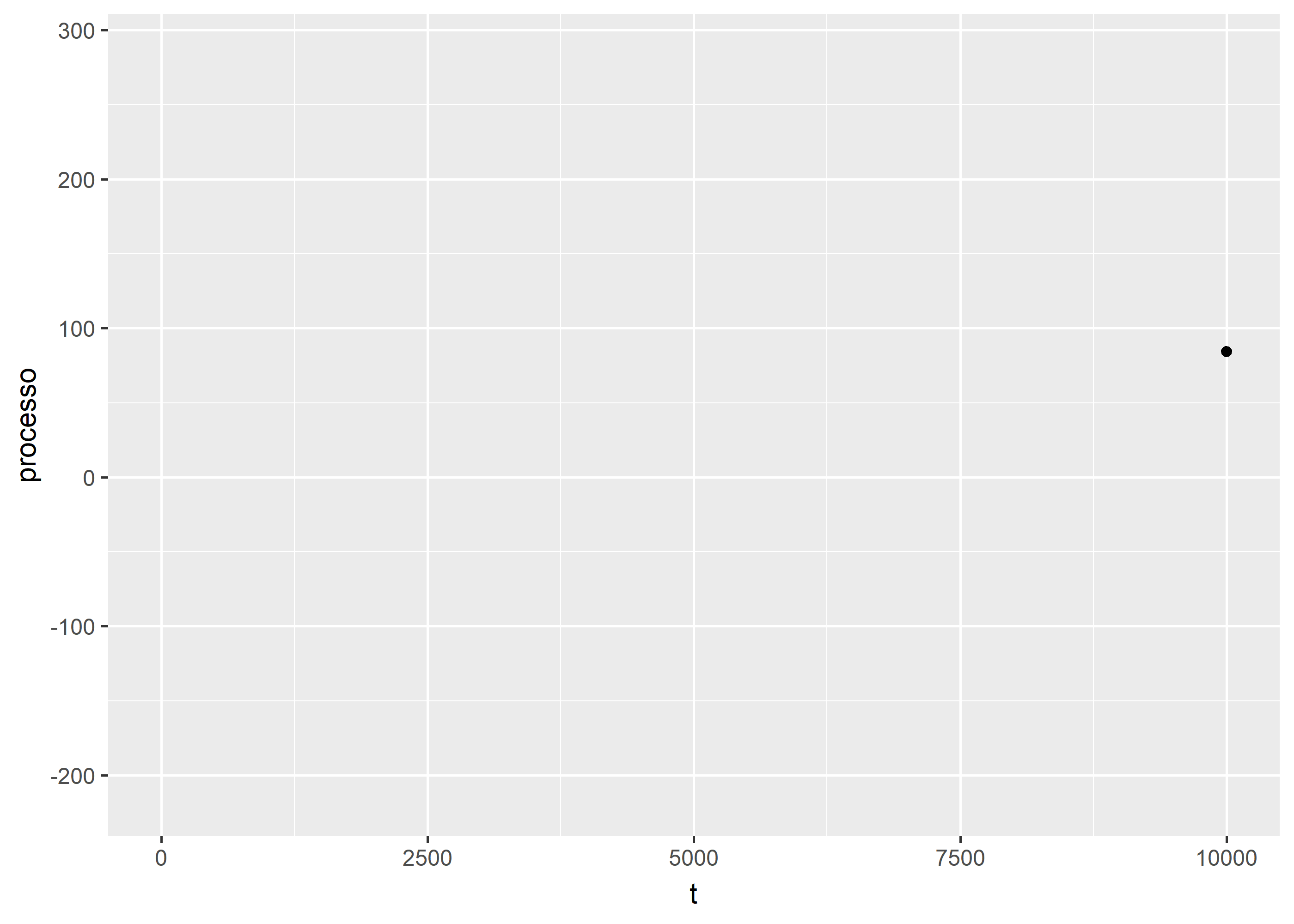
processos %>%
ggplot(aes(x = t, y = processo)) +
geom_point() 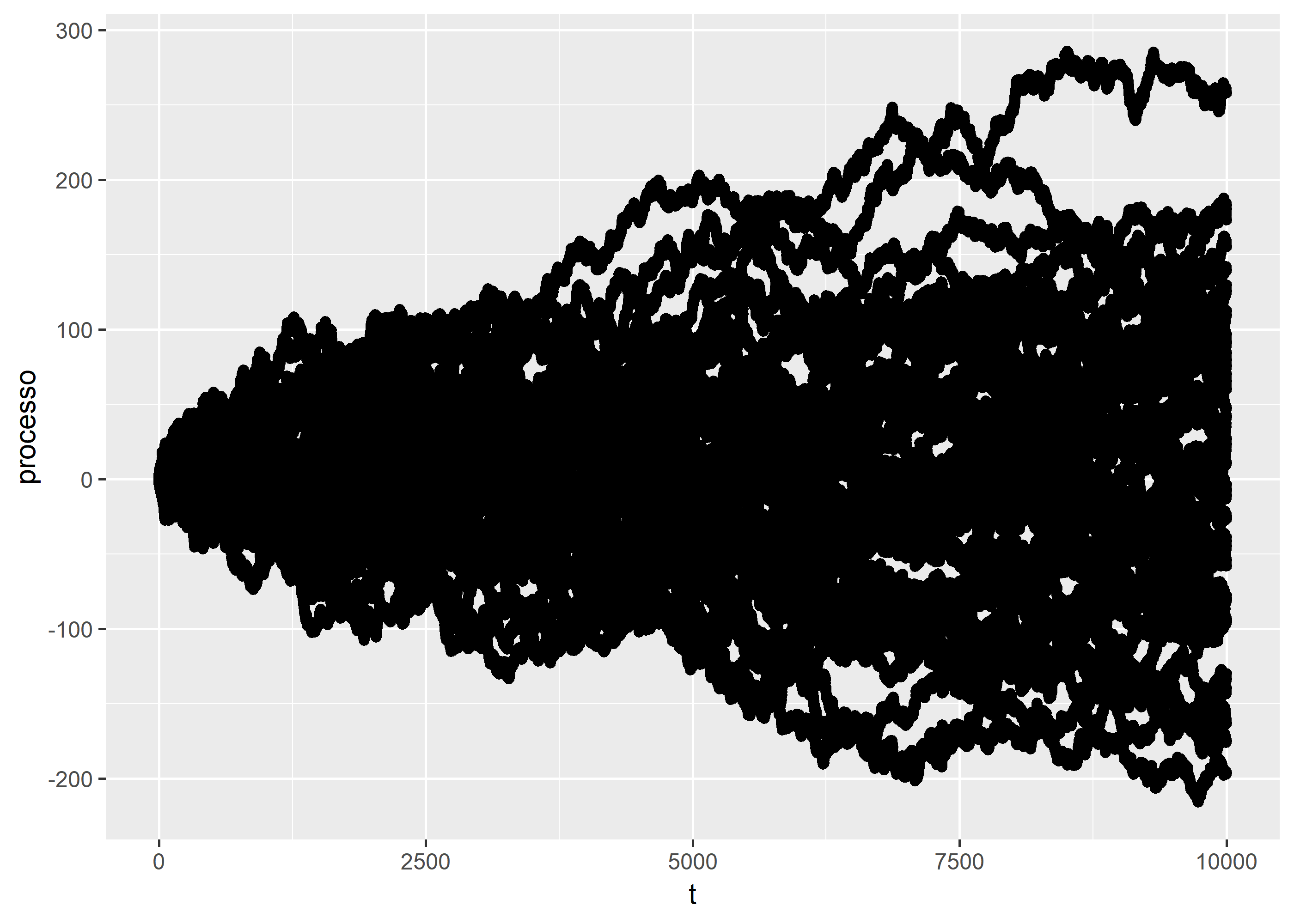
De fato, parece que conseguimos o
bservar o comportamento previsto na teoria. Em breve revisitarei esse post falando de processos AR1 que regridem assintoticamente a um patamar e mostrar como isso está conectado com o Teorema do Ponto Fixo de Banach - de que já falei aqui no blog.