Medindo a inércia da inflação brasileira com Rolling Window Regression
Eu confesso que tenho certa preguiça de macroeconomia, mas gosto bastante de econometria e programar exercícios de estimação. Dia desses me veio à mente Rolling Window Regression. Estimamos coeficientes de um modelo dentro de uma subamostra dos dados, movemos a subamostra em paralalo para um momento posterior no tempo e reestimamos o modelo. O que sai daí é uma série temporal de coeficientes estimados - efetivamente um processo estocástico porque é uma sequência de variáveis aleatórias. Vou mostrar isso funcionando estimando a inércia inflacionária no Brasil com um AR1.
library(ggplot2)
library(dplyr)
library(BETS)
ipca <- BETSget(433,
from = "1998-09-01",
data.frame = TRUE) # IPCA desde outubro de 98
ipca %>%
ggplot(aes(x = date, y = value)) +
geom_line(size = 1.2) +
xlab("Tempo") +
ylab("Variação Mensal do IPCA (em %)") +
geom_hline(yintercept = mean(ipca$value)) + # linha horizontal na média
labs(caption = "Elaboração: Pedro Cavalcante") 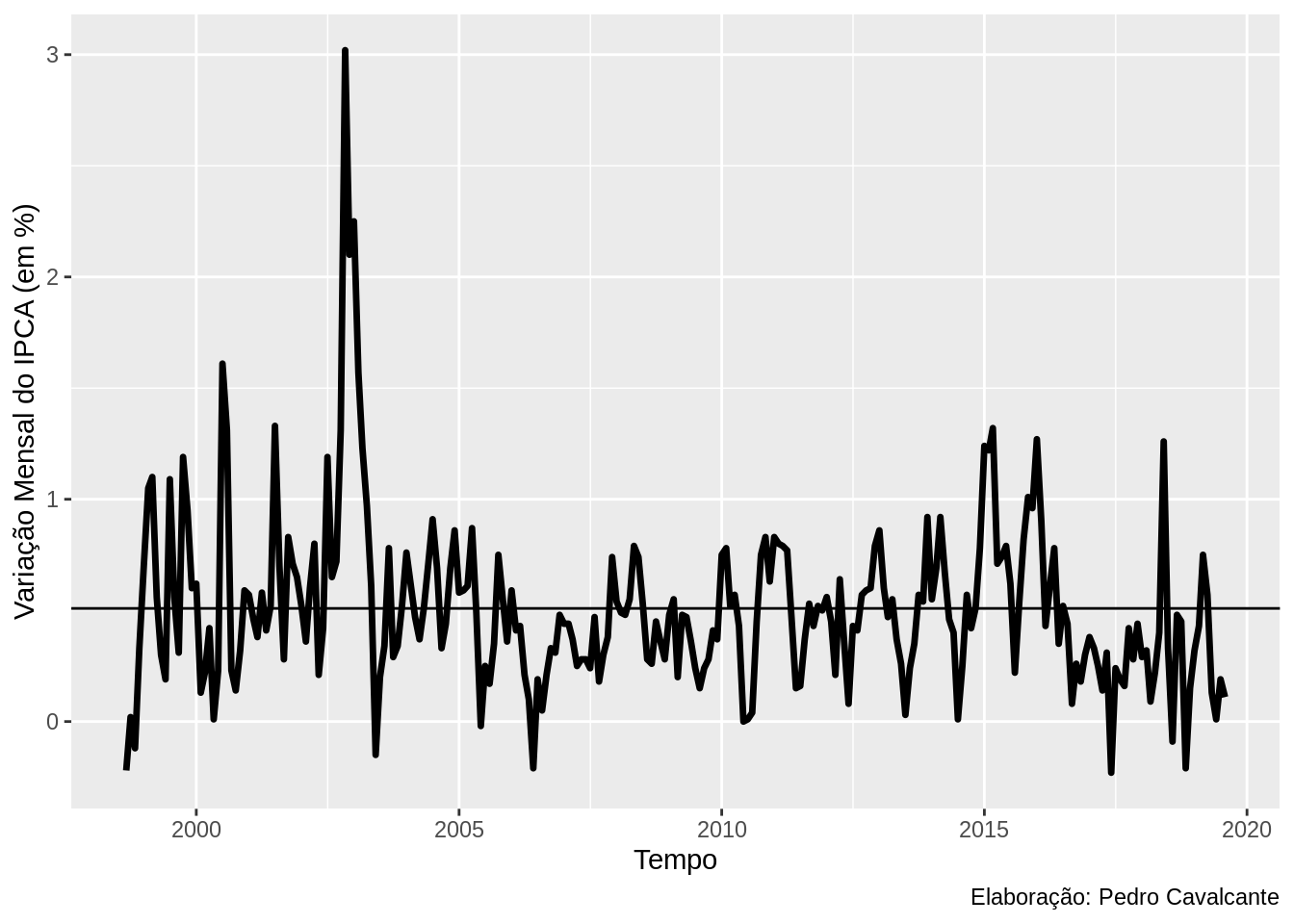
Se notarmos a inflação no período \(t\) como \(\pi_t\), modela-la como um processo autoregressivo de ordem \(k\) é estimar o seguinte modelo com \(k=1\):
\[\pi_t = \phi_0 + \sum_{i=1}^{k} \phi_i \pi_{t-i} + \epsilon_t\]
base <- ipca %>% as_tibble()
base$primeiro_lag <- base$value %>% dplyr::lag()
coeficientes <- vector()
janela <- 12*5 # número de meses em cada janela
for(i in janela:nrow(base)) {
window <- base[(i-janela):i,] # pegamos uma janela
modelo <- lm(value ~ primeiro_lag,
data = window) # estimamos o AR1
coeficientes[i] <- modelo$coefficients[2] # armazenamos o coeficiente estimado
}
coeficientes <- tibble(coef = coeficientes,
tempo = base$date[1:length(coeficientes)]) %>%
filter(!is.na(coef))
coeficientes %>%
ggplot(aes(y = coef, x = tempo)) +
geom_line(size = 1.2) +
scale_x_date(limits = c(as.Date("2003-01-01"), as.Date("2020-01-01"))) +
labs(title = "Evolução do coeficiente de um AR(1)",
subtitle = "Variável explicada é variação mensal do IPCA, regressão em janelas de 5 anos") +
ylab("") +
geom_smooth(method = "loess")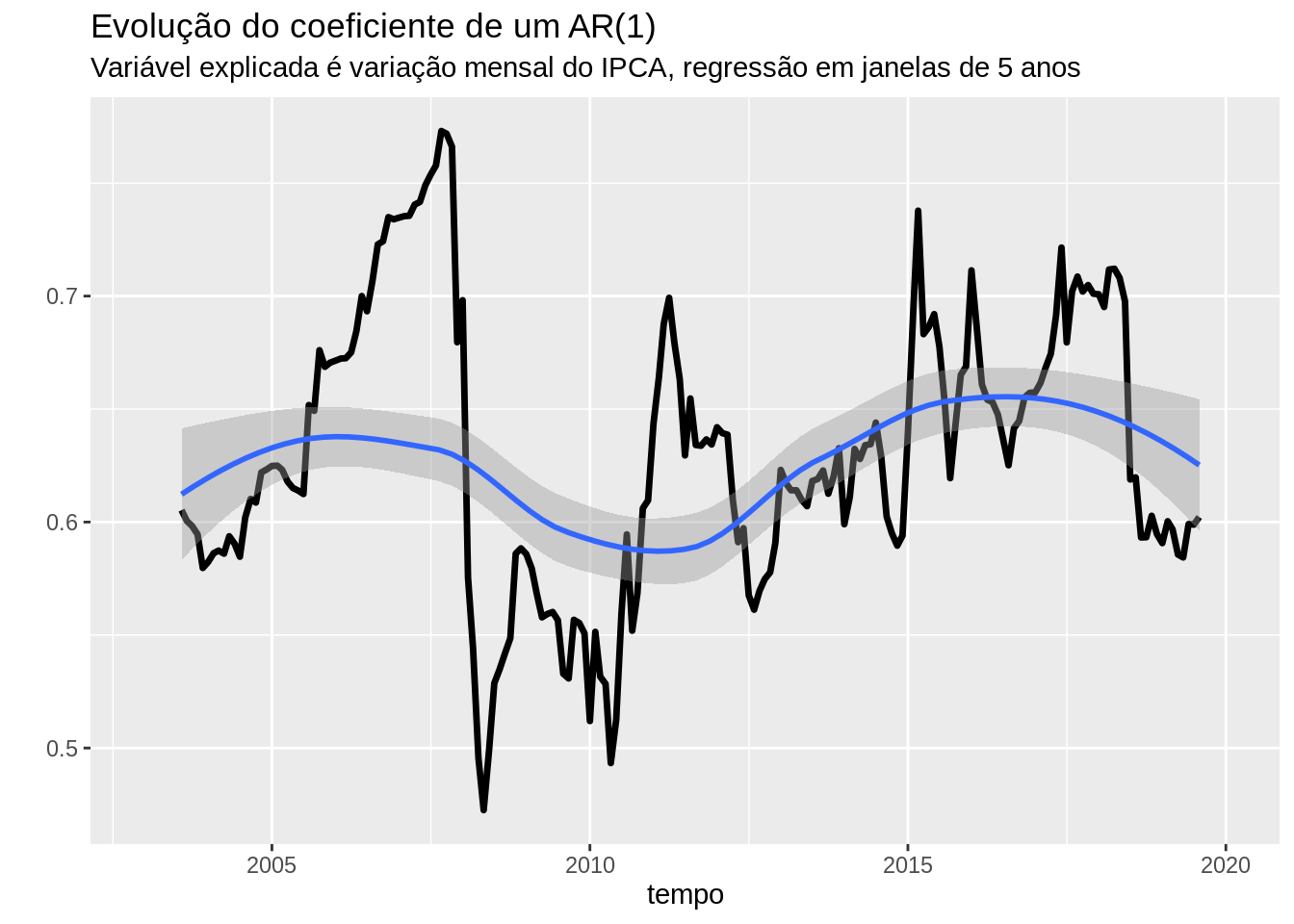
Como esperado a inércia segue uma tendência de alta nos anos da Nova Matriz.