Regredindo séries temporais aleatórias para quem gosta de regressão

Para você que gosta de regressão eu pensei em um exercício bem boboca sobre séries temporais que ilustra muito bem o motivo por trás de perguntar: “essa série é estacionária?” ao ver uma regressão com dados observados ao longo do tempo. Se você não sabe o que são séries temporais ou processos estacionários este post talvez seja um tanto quanto etéreo para você e eu seriamente recomendo que você leia esse aqui ou este outro no lugar.

Bem, vamos direto ao ponto. Vou simular dois processos, um \(x_t = 0.02t + 0.8x_{t-1} + \epsilon_t\) e \(y_t = 0.015t + 0.7y_{t-1} + \mu_t\) onde \(\epsilon_t, \mu_t \sim N(0,0.5)\). Você pode observar que não são determinísticos, seus choques tem covariância nula e que geralmente falando não ficam parados com a passagem do tempo. Não é razoável supor que regridam a um patamar estável de longo prazo - PIB é um exemplo do mundo real com este tipo de comportamento.

library(tibble)
library(ggplot2)
library(dplyr)

n <- 1000 # tamanho da amostra

dados <- tibble(x = double(length = n),
                y = double(length = n),
                t = 1:n)

nrow(dados)

## [1] 1000

Geramos um tibble vazio com \(1000\) observações vazias (porém tipadas para números reais) em dois vetores. Agora simulamos os processos:

dados$x[1] <- 20 # condições iniciais
dados$y[1] <- 30

for(i in 2:n) {
  
  dados$x[i] <- .02*dados$t[i] + 0.8*dados$x[(i-1)] + rnorm(n = 1, sd = 5)
  dados$y[i] <- .015*dados$t[i] + 0.7*dados$y[(i-1)] + rnorm(n = 1, sd = 5)
  
}

dados %>%
  ggplot(aes(x = t)) +
  geom_line(aes(y = x), size = 1.2, alpha = .7) +
  geom_line(aes(y = y), size = 1.2, alpha = .7) +
  labs(y = "",
       x = "Tempo") +
  theme_minimal()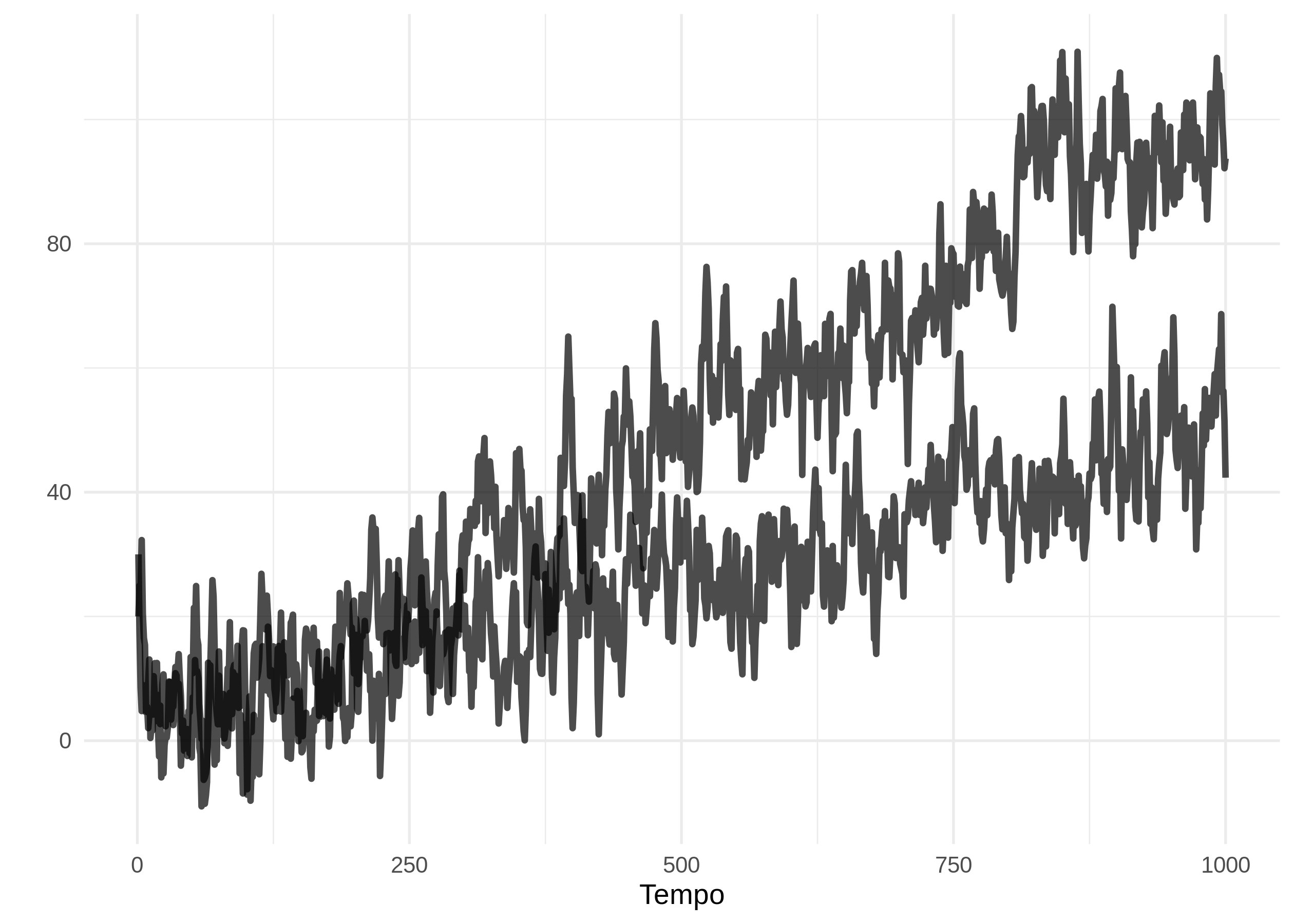

Agora vamos fazer um simples exercício, uma regressão linear.

modeloRuim <- lm(y ~ x, 
                 data = dados)

summary(modeloRuim)

## 
## Call:
## lm(formula = y ~ x, data = dados)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -21.5360  -5.6746  -0.1285   5.6155  27.2958 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 4.144688   0.478827   8.656   <2e-16 ***
## x           0.430371   0.008147  52.826   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.044 on 998 degrees of freedom
## Multiple R-squared:  0.7366, Adjusted R-squared:  0.7363 
## F-statistic:  2791 on 1 and 998 DF,  p-value: < 2.2e-16

Um impressionante R2 e um coeficiente mais do que significante! Que curioso que duas séries que aleatórias com tendências se expliquem, aparentemente. Ora, só pode ser porque escolhi alguma combinação pecualiar de parâmetros, ou talvez os choques tenham sido aleatórios de maneira bem específica. Vamos sanar essa dúvida simulando uma penca de séries, regredindo-as e guardando o R2. Vamos fazer os parametros variarem aleatoriamente.

m <- 500 # número de modelos
n <- 500 # tamanho da amostra

simulacao <- tibble(R2 = double(length = m))
  
  for(i in 1:m) {
  
  dados <- tibble(x = double(length = n),
                  y = double(length = n),
                  t = 1:n)
    
    
  dados$x[1] <- 20 # condições iniciais
  dados$y[1] <- 30
  
  param1 <- runif(n = 1, 0.01, .1) 
  param2 <- runif(n = 1, 0.01, .1)
  
  param3 <- rnorm(n = 1, mean = .8, sd = .15)
  param4 <- rnorm(n = 1, mean = .7, sd = .15)
  
      for(j in 2:n) {
      
      dados$x[j] <- param1*dados$t[j] + param3*dados$x[(j-1)] + rnorm(n = 1, sd = 5)
      dados$y[j] <- param2*dados$t[j] + param4*dados$y[(j-1)] + rnorm(n = 1, sd = 5)
      
      }


  modeloRuim <- lm(y ~ x, 
                   data = dados)
  
  simulacao$R2[i] <- summary(modeloRuim)$r.squared
  
  }

simulacao %>%
  ggplot(aes(x = R2)) +
  geom_histogram(aes(y = ..density..), binwidth = .05) +
  geom_vline(xintercept = mean(simulacao$R2), size = 1.2) + # veta vertical na média
  labs(title = "Distribuição dos R2 de regressões entre duas séries aleatórias com tendência",
       subtitle = "Simulação com 500 processos tendo 500 obs e parâmetros aleatórios",
       caption = "Elaboração: Pedro Cavalcante. Disponível em azul.netlify.com",
       x = "R2 das regressões",
       y = "")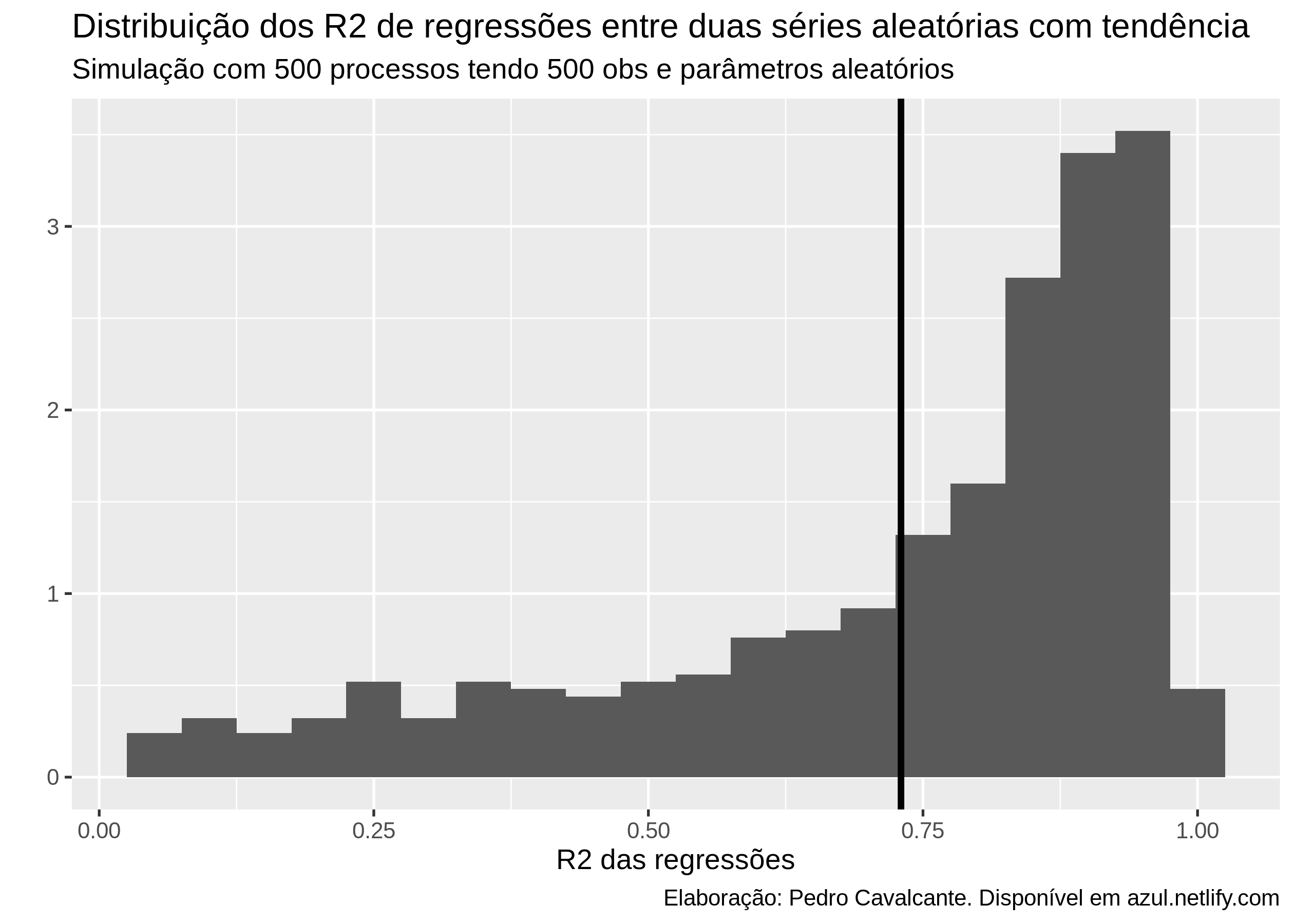

Oh nossa que surpresa, essas regressões são todas espúrias e qualquer um que tenha estudado 15 minutos de séries temporais sabe disso, fascinante não?

Deixo aí para quem gosta de uma regressão…