Enunciado

Existem várias combinações de rigor e generalidade possíveis em um enunciado válido deste teorema. Podemos falar do Teorema Central do Limite em Martingales, em processos dependentes, em várias dimensões… Mesmo em um contexto mais simples, com amostras \(i.i.d.\) e uma dimensão há formas diferentes de expor a convergência. Vou optar pelo enunciado mais simples que conheço.

• Teorema (Central do Limite): Seja \((X_1, X_2,...,X_n)\) uma amostra aleatória \(i.i.d.\) com média \(\mu\) e variância \(\sigma^2\) finitas. Então a média amostral, à medida que o tamanho \(n\) da amostra aumenta, converge em distribuição para uma normal com média \(\mu\) e variância \(\frac{\sigma^2}{n}\).

Em símbolos:

\[\bar{X} \xrightarrow[n]{d} N(\mu, \frac{\sigma^2}{n}) \] Podemos reformular e mirar em uma convergência à uma normal padrão. Definda \(Z := \frac{\sum_{i=1}^n X_i - n\mu}{\sigma \sqrt{n}}\). Subtraímos a média e dividimos pelo desvio padrão, então efetivamente normalizamos a variável¹. O Teorema afirma que \(Z\) converge em distribuição para uma normal padrão.

Observe que não falamos da distribuição de \(X\) em momento algum. Médias de amostras com a mesma distribuição convergem à normalidade para qualquer distribuição que \(X\) tenha.

Simulações

Vamos começar desenhando a estrutura dos nossos dados.

library(tibble)
library(dplyr)

n <- 5000 # número de médias a serem calculadas
m <- 5000 # tamanho de cada amostra cuja média será calculada

simulacao <- tibble(indice = 1:n,
                    exponencial = double(length = n),
                    uniforme = double(length = n),
                    tStudent = double(length = n),
                    fFisher = double(length = n))

Agora com um tibble vazio nos esperando, vamos preenche-lo.

set.seed(1234)

for(i in 1:n) {
  
  simulacao$exponencial[i] <- rexp(n = m) %>% mean()
  simulacao$uniforme[i] <- runif(n = m) %>% mean()
  simulacao$tStudent[i] <- rt(n = m, df = 2) %>% mean() # média de uma t com 2 graus de liberdade
  simulacao$fFisher[i] <- rf(n = m, df1 = 2, df2 = 4) %>% mean() # média de uma F(2, 4)
  
  
}

Afinal, nossos dados tem cara de serem normais?

library(ggplot2)

simulacao %>% 
  ggplot(aes(x = exponencial)) +
  geom_histogram(aes(y = ..density..), fill = "blue", alpha = .7) +
  geom_density(size = 1.5, alpha = .9, color = "red") +
  theme_minimal() +
  labs(title = "Histograma das médias de 5000 amostras de 5000 tiradas de uma exponencial",
       x = "",
       y = "",
       caption = "Elaboração: Pedro Cavalcante. Disponível em azul.netlify.com")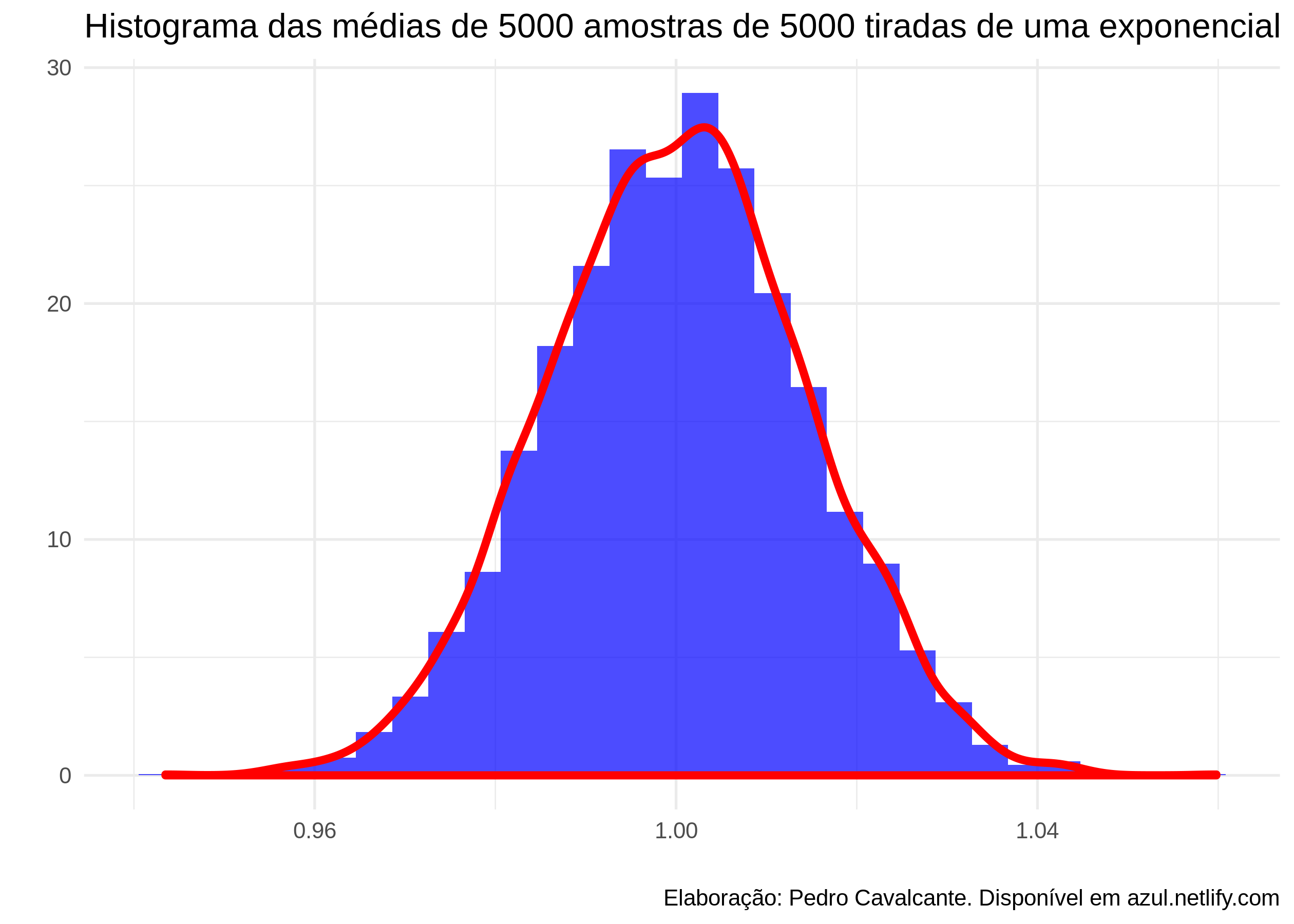

A distribuição das médias parece bem normal. E mais, centrada justamente em \(1\), a média da exponencial que geramos. E as outras distribuições?

simulacao %>% 
  ggplot(aes(x = tStudent)) +
  geom_histogram(aes(y = ..density..), fill = "blue", alpha = .7) +
  geom_density(size = 1.5, alpha = .7, color = "red") +
  theme_minimal() +
  labs(title = "Densidade das médias de 5000 amostras de 1000 tiradas de uma t-Student",
       x = "",
       y = "",
       caption = "Elaboração: Pedro Cavalcante. Disponível em azul.netlify.com")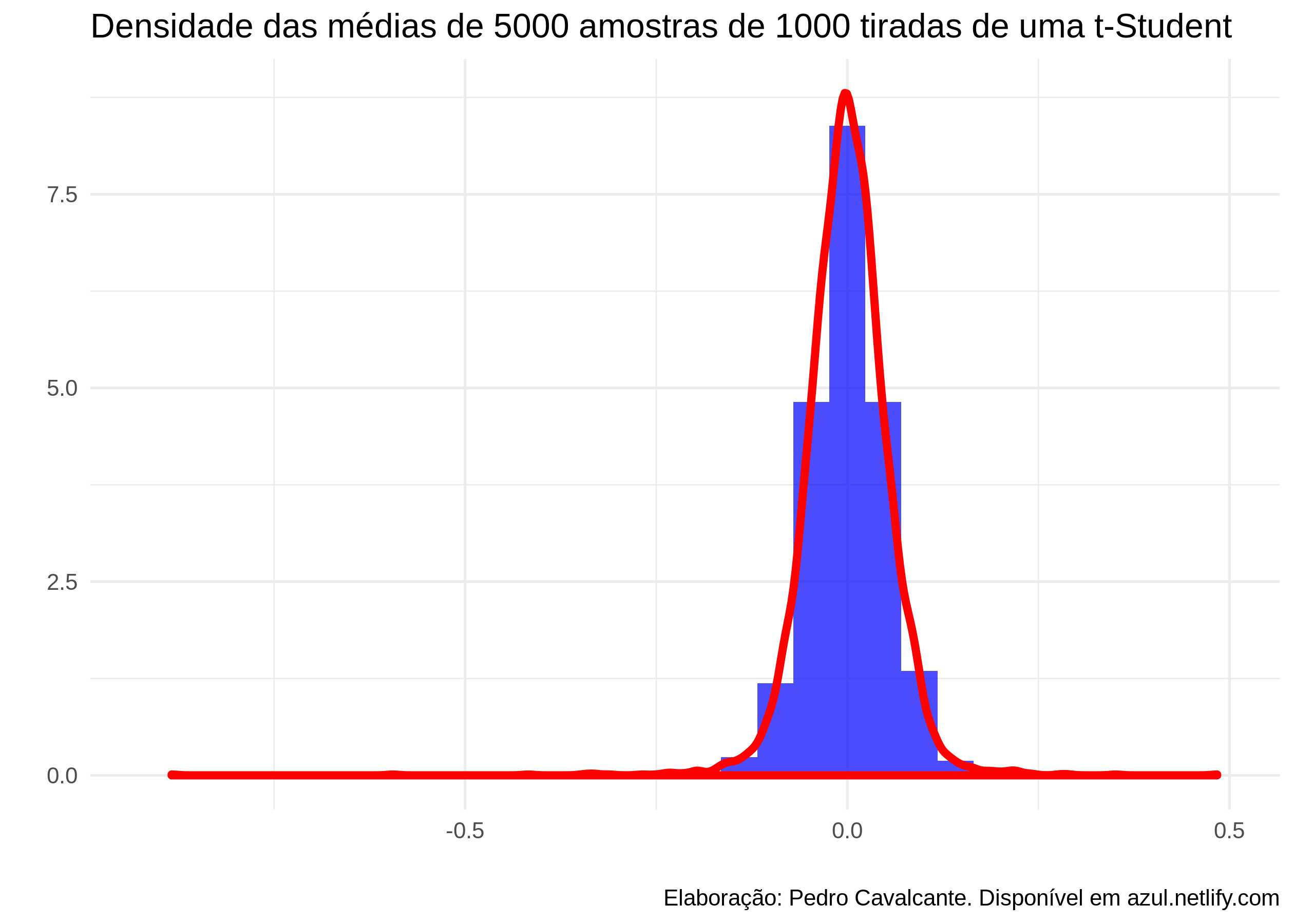

Sugiro ao leitor replicar o exercício e ver como ficam os histogramas das outras distribuições. Vamos agora ser um pouco mais assertivos. Normalizerei os dados para média \(0\) e variância unitária testeremos normalidade com o teste Kolmogorov-Smirnoff em pedaços da amostra sucessivamente maiores. Afinal, de fato a estatística do teste está aumentando à medida que aumentamos a amostra - e portanto - nossas médias setão convergindo em distribuição?

testes <- tibble(indice = 3:n,
                 pUniforme = double(length = n-2),
                 pT = double(length = n-2),
                 pF = double(length = n-2)
                 )

Com outro tibble pronto podemos preenche-lo:

for(i in 3:nrow(testes)) {
  
  janela <- simulacao %>% 
    filter(indice <= i) %>% # selecionamos apenas os índices até o atual
    transmute(uniforme = (uniforme - mean(uniforme)/sd(uniforme)),
              tStudent = (tStudent - mean(tStudent))/sd(tStudent),
              fFisher = (fFisher - mean(fFisher))/sd(fFisher))
  

  testes$pUniforme[i] <- ks.test(x = janela$uniforme, "pnorm")$p.value
  testes$pT[i] <- ks.test(x = janela$tStudent, "pnorm")$p.value
  testes$pF[i] <- ks.test(x = janela$fFisher, "pnorm")$p.value
  
  
}

library(tidyr)

testes %>%
  pivot_longer(pUniforme:pF, 
               names_to = "distro",
               values_to = "p") %>%
  ggplot(aes(x = indice, color = distro, y = p)) +
  geom_line(size = 1.5, alpha = .7) +
  labs(title = "Evolução do p-valor do teste KS para normalidade",
       x = "Amostra",
       y = "p-valor",
       caption = "Elaboração: Pedro Cavalcante. Disponível em azul.netlify.com") +
  theme_minimal() +
  scale_y_continuous(label = scales::percent)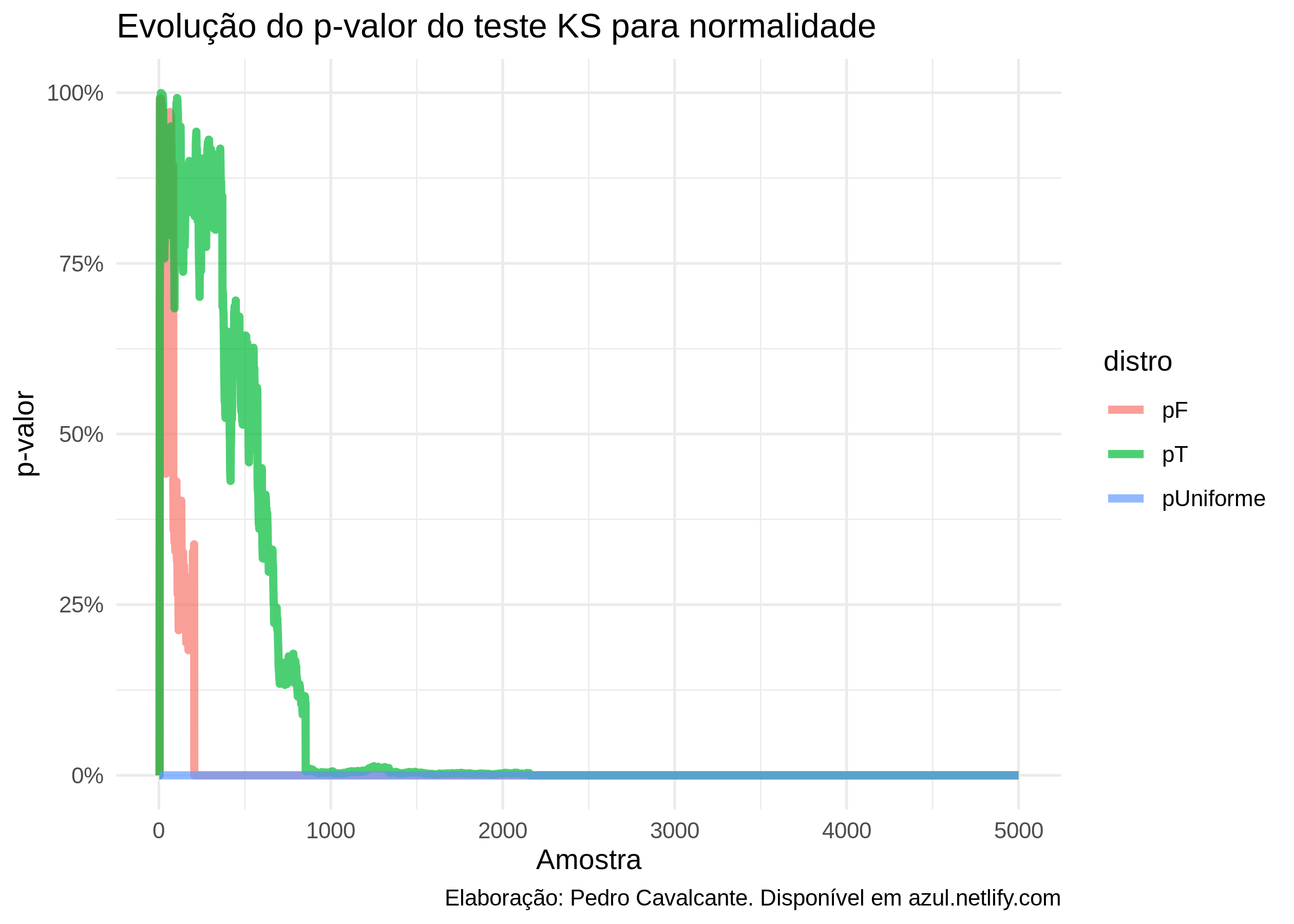

A convergência demora mais para algumas distribuições do que outras, mas a tendência de queda é mais do que clara!