Provavelmente vocês já se depararam com a situação de que você precisa usar erros que corrigem para o fato do erro ser possivelmente autocorrelacionados ou heterocedásticos. Enquanto a parte de heterocedasticidade é bastante interessante, esse post vai focar no problema de erros consistentes para processos correlacionados.

Para começar, suponha que temos um processo estocástico \(u_t\) que é autocorrelacionado. Suponha que queremos calcular a média do processo, então teremos \(1/T\sum_{t=1}^{T} u_t\). Agora, qual a variância da média? No caso iid, nós faríamos:

\[Var(1/T\sum_{t=1}^T u_t) = 1/T^2 Var(\sum_{t=1}^T u_t) = 1/T^2 \sum_{t=1}^T Var(u_t) = \sigma_u^2/T\]

Eu impunemente passei o somatório para fora da variância porque o processo é iid. Se \(u_t\) tiver autocorrelação, nós vamos ter de considerar as covariâncias:

\[Var(1/T\sum_{t=1}^T u_t) = 1/T^2 Var(\sum_{t=1}^T u_t) = 1/T^2 Var(u_t + u_{t+1} + u_{t+2}) = \]

\[=1/T^2(TVar(u_t) + (T-1) Cov(u_t,u_{t-1}) + (T-2)Cov(u_t,u_{t-2}) + ...)\]

Veja que eu estou trabalhando com processos estacionários, e isso me permite dizer que \(Cov(u_t,u_{t+1}) = Cov(u_{t+1},u_{t+2})\) etc.

Que teremos T covariâncias parece simples, mas como eu sei que teremos T-1 covariâncias entre dois períodos sequenciais? Veja que como a amostra está limitada até T, todos os períodos menos o T tem um vizinho seguinte: portanto T-1 covariâncias seguintes. Já para \(Cov(u_t,u_{t+2})\), tanto o período \(T\) quanto o período \(T-1\) não tem vizinhos para frente: logo temos \((T-2) Cov(u_t,u_{t+2})\). Etc etc. Isso exige uma certa imaginação, eu admito.

O mais incrível é que nós também temos que considerar as covariâncias para trás, ou seja \(Cov(u_t,u_{t-1})\), \(Cov(u_t,u_{t-2})\) etc. Felizmente, graças ao fato de o processo ser estacionário de segunda ordem, temos que \(Cov(u_t,u_{t-1}) = Cov(u_t,u_{t+1})\) e portanto:

\[Var(1/T\sum_{t=1}^T u_t) = 1/T^2(TVar(u_t)+2(T-1)Cov(u_t,u_{t-1}) + ...)\]

Ou seja, a variância da média de \(u_t\) depende da soma das covariâncias do processo. Antes de prosseguirmos, só um pequeno detour. Para deixar a notação menos carregada, faça \(\gamma_0 = var(u_t)\), \(\gamma_1 = cov(u_t,u_{t-1})\),…, \(\gamma_j = cov(u_t,u_{t-j})\), e a expressão acima pode ser reescrita como:

\[\frac{2}{T}\left(\sum_{t=0}^{T-1} \gamma_t - 1/T\sum_{j=0}^{T-1} j\gamma_j\right)\]

Reescale tudo por \(T\), que é o equivalente a multiplicar o somatório por \(1/\sqrt{T}\), como a gente faria para aplicar o teorema central do limite, para obter:

\[2\left(\sum_{t=0}^{T-1} \gamma_t - 1/T\sum_{j=0}^{T-1} j\gamma_j\right)\]

Logo a variância assintótica ($T ) depende do somatório das auto-covariâncias - e das covariâncias daqui até o infinito! Obviamente, nós não temos nenhuma chance de conseguir isso.

Isso gera também o seguinte problema: podemos ter auto-covariâncias negativas (um ar(1) com parâmetro negativo vai gerar autocorrelações pares que são positivas mas ímpares negativas). Usando a autocovariância amostral, podemos ter isso. Por exemplo, vamos trabalhar com um AR(1) com parâmetro 0.5 e a inovação tem variância 1. Eu vou usar 50 observações. Veja que se truncassemos entre os lags 10 e 20, teríamos uma variância negativa:

set.seed(9872)

T <- 50 #numero de periodos
k <- 40#numero de lags
rho <- 0.5 #parametro do processo AR(1)

u <- rep(0,T)

for(i in 1:(T-1)){
  u[i+1] <- rho*u[i] + rnorm(1)  
}

acf <- Acf(u,plot=F, type = "covariance",lag.max = k)

var_partial <- rep(0,k+1)
var_partial[1] <- T*acf$acf[1]

for(i in 2:(k+1)){
  var_partial[i] <- var_partial[i-1] + 2*(T-i+1)*acf$acf[i]
}

var_partial <- var_partial/T^2

df <- data.frame(lag = 0:k,var = var_partial)

pp <- ggplot(df,aes(lag,var))

pp + geom_point() + geom_hline(aes(yintercept=0))

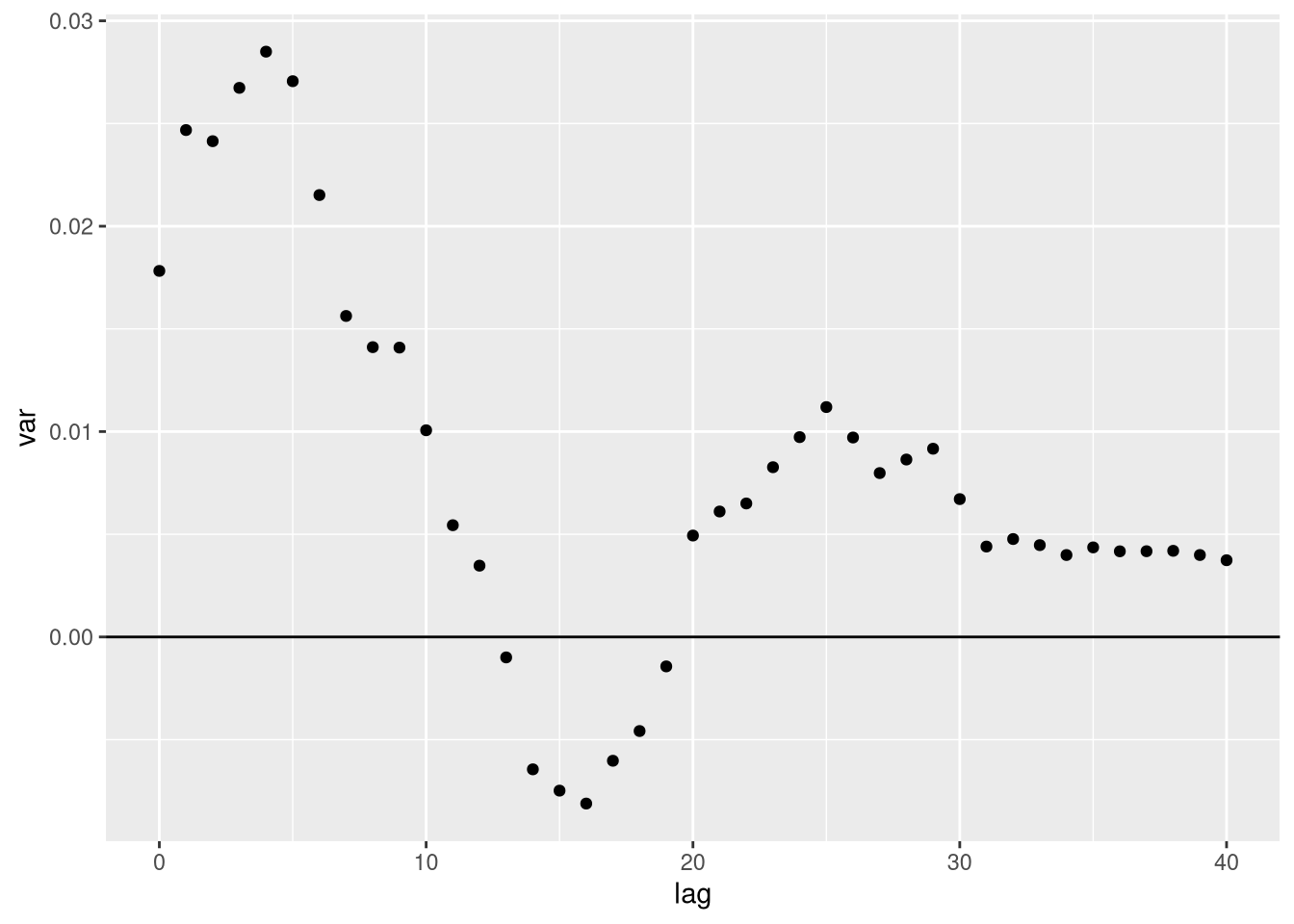
Obviamente, variâncias não são negativas. Nossa amostra só permite calcular até a autocovariância \(T\), e com precisão cada vez pior (a autocovariância em T só tem uma observação, enquanto a autocovariância de um lag tem T-1 observações). Nós precisamos garantir que a variância vai ser positiva.

A variância calculada usando HAC faz isso dando pesos de maneira esperta para cada autocovariância: eles envolvem argumentos de estatística não paramétrica e por isso eu não vou entrar em detalhes. Existem várias possibilidades de Kernel, e Kernel exige a seleção de um parâmetro de bandwidth.

Veja que no caso de erros robustos apenas a heterocedasticidade, esse tipo de argumento não precisa ser aplicado: o problema é que em processos de série temporal os erros vão estar correlacionados. Usar matrizes robustas a heterocedasticidade apenas não envolvem argumentos de métodos estatísticos não paramétrico.

Em geral nós usamos erro padrão HAC para testar uma hipótese em regressão em que podemos ter erros autocorrelacionados. Quando fazemos testes a 5%, nós estamos controlando a probabilidade de cometer um erro do tipo I (i.e. rejeitar a hipótese nula quando ela é verdadeira) de no máximo 5%. Mais que isso é sinal que nosso teste tem algum problema. Para ilustrar isso, eu vou fazer algumas simulações monte carlo (como de praxe).

Para ficar fácil, eu vou trabalhar com uma regressão com um único coeficiente, que vai ser zero, sempre. Vão mudar o tamanho da amostra e o processo gerador de dados. Eu vou sempre testar 3 maneiras: ignorando o problema, usando o padrão do pacote sandwhich (que é o sugerido pelo Andrews), e a primeira HAC sugerida, o Newey-West.

Para começar, vamos testar o caso em que nós somos meramente preguiçosos e colocamos erros robustos a autocorrelação sem pensar muito no tema:

s <- matrix(0,nrow = 3000,ncol=3)

for(j in 1:3000){

  uu <- rnorm(100)

  x <- rnorm(100)
  y <- uu

  reg <- lm(y~x)

  s[j,1] <- summary(reg)$coefficients[2,4]
  s[j,2] <- coeftest(reg,vcov. = vcovHAC(reg))[2,4]
  s[j,3] <- coeftest(reg,vcov. = NeweyWest(reg))[2,4]
}


tab0 <- colMeans(s < 0.05)
names(tab0) <- c("Sem correção", "HAC Default", "Newey West")
knitr::kable(tab0)

Ser preguiçoso é problemático: nós rejeitamos quase 1% a mais do que os 5% que queremos alcançar ao usar o padrão do pacote - e se usarmos a proposta do Newey West, a situação é ainda pior. Agora, vamos colocar erros auto regressivos:

s <- matrix(0,nrow = 3000,ncol=3)

for(j in 1:3000){

  uu <- arima.sim(n = 100,list(ar=c(0.5)))

  x <- rnorm(100)
  y <- uu

  reg <- lm(y~x)

  s[j,1] <- summary(reg)$coefficients[2,4]
  s[j,2] <- coeftest(reg,vcov. = vcovHAC(reg))[2,4]
  s[j,3] <- coeftest(reg,vcov. = NeweyWest(reg))[2,4]
}


tab1 <- colMeans(s < 0.05)
names(tab1) <- c("Sem correção", "HAC Default", "Newey West")
knitr::kable(tab1)

Newey-West é desastroso, com um tamanho de 8%. Ignorar o problema parece, estranhamente, a melhor estratégia! Vamos aumentar a persistência do erro colocando o parâmetro auto regressivo em 0.95 e aumentar o número de observações, o que vai ajudar na convergência dos estimadores HAC:

s <- matrix(0,nrow=3000,ncol=3)

for(j in 1:3000){

  uu <- arima.sim(n = 1000,list(ar=c(0.95)))

  x <- rnorm(1000)
  y <- uu

  reg <- lm(y~x)

  s[j,1] <- summary(reg)$coefficients[2,4]
  s[j,2] <- coeftest(reg,vcov. = vcovHAC(reg))[2,4]
  s[j,3] <- coeftest(reg,vcov. = NeweyWest(reg))[2,4]
}

tab2 <- colMeans(s < 0.05)
names(tab2) <- c("Sem correção", "HAC Default", "Newey West")
knitr::kable(tab2)

Mais um caso, com erro seguindo um MA:

s <- matrix(0,nrow=3000,ncol=3)

for(j in 1:3000){

  uu <- arima.sim(n = 100,list(ma=c(0.8)))

  x <- rnorm(100)
  y <- uu

  reg <- lm(y~x)

  s[j,1] <- summary(reg)$coefficients[2,4]
  s[j,2] <- coeftest(reg,vcov. = vcovHAC(reg))[2,4]
  s[j,3] <- coeftest(reg,vcov. = NeweyWest(reg))[2,4]
}


tab3 <- colMeans(s < 0.05)
names(tab3) <- c("Sem correção", "HAC Default", "Newey West")
knitr::kable(tab3)

Vamos aumentar o número de observações para mil:

s <- matrix(0,nrow=3000,ncol=3)

for(j in 1:3000){

  uu <- arima.sim(n = 1000,list(ma=c(0.8)))

  x <- rnorm(1000)
  y <- uu

  reg <- lm(y~x)

  s[j,1] <- summary(reg)$coefficients[2,4]
  s[j,2] <- coeftest(reg,vcov. = vcovHAC(reg))[2,4]
  s[j,3] <- coeftest(reg,vcov. = NeweyWest(reg))[2,4]
}


tab3 <- colMeans(s < 0.05)
names(tab3) <- c("Sem correção", "HAC Default", "Newey West")
knitr::kable(tab3)

Veja que de maneira geral, os testes no caso de erros autocorrelacionados tem problemas de tamanho. Newey West gera resultados preocupantes - no nosso primeiro e segundo exemplo, a porcentagem de erros tipo I foi 8% quando estavamos usando o teste para obter um erro de tipo I em 5% dos testes. Ignorar o problema não parece uma boa estratégia, apesar de os resultados serem razoáveis em muitos casos. Eu fiz só alguns exemplos muito simples e isso pode gerar resultados que parecem bons. O padrão do sandwich nos dá resultados razoáveis para quase todos os DGPs.

Veja que os efeitos no mundo real disso são bem simples: nós rejeitamos a hipótese nula com frequência diferente da que estamos controlando.