Mas e a indústria?
Dia desses li coisas tristes. A narrativa era de que alguns setores são por alguma propriedade vinda dos céus (alguns dirão ah mas e a complexidade… e eu direi que são eles os que invejam os físicos) mais “importantes” que outros e que, de fato, o processo de desenvolvimento econômico é sim substituir participação de setores menos complexos por outros mais complexos. A magia, o pulo do gato, o estopim de um ciclo virtuoso de crescimento estaria em produzir menos soja e mais massa proteica, menos ferro e mais carros, menos bananas e mais microchips… Qualquer semelhança com as viúvas do regime militar não é coincidência.
Este blogueiro discorda e gostaria de mostrar (i) como R (e mais geralmente, programação) facilitam nossa vida e (ii) que composição setorial não é lá grandes coisas. Decidi usar a 10-Sector Database com dados de emprego e produto a nível de setor em vários países e a Penn World Tables para calcular o câmbio real. A 10-Sector tem um formato bem esquisito. Você recebe um dataset em que cada linha é uma combinação de ano-país-variável, em que as variáveis podem ser algumas medidas de valor adicionado ou população empregada no setor. Ela entrega 11 colunas, 10 representando setores e uma o agregado.
O leitor rapidamente percebe que são dados com uma estrutura um tanto quanto curiosa, nem um pouco tidy em que cada coluna é uma variável e cada linha uma observação. Tomeremos o cuidado de colocar os dados neste formato. Vamos antes inspecionar a documentação, contida na primeira planilha do arquivo de excel em que a base é disponibilizada.
knitr::opts_chunk$set(message = FALSE, warning = FALSE, dpi = 320)
library(dplyr)
library(purrr)
library(ggplot2)
library(tidyr)
library(rlang)
library(rio)
library(magrittr)
library(knitr)
library(pwt9)
rio::import("https://www.rug.nl/ggdc/docs/10sd_jan15_2014.xlsx",
sheet = 1) %>%
as_tibble() %>%
head(n = nrow(.)) %>%
kable() # inspecionando a documenta??o| Overview of the GGDC 10 Sector Database | …2 |
|---|---|
| Economic activities distinguished | 1. Agriculture, hunting, forestry and fishing (AtB); |
| (ISIC rev. 3.1 code): | 2. Mining and quarrying (C); |
| NA | 3. Manufacturing (D); |
| NA | 4. Electricity, gas and water supply (E); |
| NA | 5. Construction (F); |
| NA | 6. Wholesale and retail trade, hotels and restaurants (GtH); |
| NA | 7. Transport, storage, and communication (I); |
| NA | 8. Finance, insurance, real estate and business services (JtK); |
| NA | 9. Government services (LtN); |
| NA | 10. Community, social and personal services (OtP) |
| NA | NA |
| Variables included: | Persons engaged (in thousands); |
| NA | Gross value added at current national prices (in millions); |
| NA | Gross value added at constant 2005 national prices (in millions); |
| NA | NA |
| Countries included: | Sub-Saharan Africa: |
| NA | Botswana, Ethiopia, Ghana, Kenya, Malawi, Mauritius, Nigeria, Senegal, South Africa, Tanzania, and Zambia |
| NA | Middle East and North Africa: |
| NA | Egypt, Morocco |
| NA | Asia: |
| NA | China, Hong Kong (China), India, Indonesia, Japan, Korea (Rep. of), Malaysia, Philippines, Singapore, Taiwan, Thailand |
| NA | Latin America: |
| NA | Argentina, Bolivia, Brazil, Chile, Colombia, Costa Rica, Mexico, Peru, Venezuela |
| NA | North America: |
| NA | United States of America |
| NA | Europe: |
| NA | West Germany, Denmark, Spain, France, United Kingdom, Italy, the Netherlands, and Sweden |
| NA | NA |
| Time period: | 1950 – 2013 |
| Notes: starting date of time series varies across variables and countries depending on data availability. | NA |
Beleza, sabemos agora que a variável de Valor Adicionado a Preços Constantes de 2005 está na moeda local e que a variável com nível de emprego está em milhares. Estamos interessados nelas.
(tenSector <- rio::import("https://www.rug.nl/ggdc/docs/10sd_jan15_2014.xlsx", sheet = 2) %>%
as_tibble() %>%
filter(Variable == "VA_Q05" | Variable == "EMP") %>% # mant?m n?vel de emprego e valor adicionado
select(-`Region code`) %>% # redundante e com nome n?o-regular, melhor tirar
gather("Sector", "Measure", -Country, -Region, -Year, -Variable) %>% # traz colunas de setores para linhas
spread("Variable", "Measure") %>% # joga as vari?veis para colunas
mutate(EMP = EMP * 1000,
VA_Q05 = VA_Q05 * 1000000,
Sector = abbreviate(Sector, minlength = 7)) %>% # aplica a escala
rename(VA = VA_Q05)) # apenas deixando o nome mais limpo## # A tibble: 27,885 x 6
## Country Region Year Sector EMP VA
## <chr> <chr> <dbl> <chr> <dbl> <dbl>
## 1 ARG Latin America 1950 Agrcltr 1799565. 16178508000.
## 2 ARG Latin America 1950 Cm,saps 410892. 7017988589.
## 3 ARG Latin America 1950 Cnstrct 314106. 9170823891.
## 4 ARG Latin America 1950 Fireabs 203838. 6359568994.
## 5 ARG Latin America 1950 Gvrnmns 824921. 23892830458.
## 6 ARG Latin America 1950 Mnfctrn 1603249. 40415974714.
## 7 ARG Latin America 1950 Mining 32719. 1993128433.
## 8 ARG Latin America 1950 SmosGDP 6543872. 137555524612.
## 9 ARG Latin America 1950 Trd,rah 889967. 24402991371.
## 10 ARG Latin America 1950 Trn,sac 425352. 7549840286.
## # … with 27,875 more rowsJá tratamos a variável com nível de emprego, agora vamos pegar a taxa de câmbio real da Penn World Table, que vem no pacote pwt9. Note também que temos dados que deveriam ser a nível de país-ano-setor, mas um dos setores aqui é o total, o PIB. Vamos tira-lo das linhas e dedicar colunas para isso, assim teremos dados consistentes.
data("pwt9.1")
# TODO adicionar explicativas
(pwt <- pwt9.1 %>%
filter(year == 2005) %>%
select(isocode, pl_gdpo, xr) %>% # queremos país, nível de preços e taxa de câmbio
as_tibble() %>%
filter(pl_gdpo > 0) %>% # removendo dados duvidosos
rename(Country = isocode) %>%
mutate(PPP = pl_gdpo * xr) %>% # obtendo o PPP
select(-pl_gdpo, -xr)) # temos um par país-câmbio real em 2005## # A tibble: 182 x 2
## Country PPP
## <fct> <dbl>
## 1 ABW 1.01
## 2 AGO 42.8
## 3 AIA 1.85
## 4 ALB 44.3
## 5 ARE 1.56
## 6 ARG 1.19
## 7 ARM 149.
## 8 ATG 2.54
## 9 AUS 1.20
## 10 AUT 0.798
## # … with 172 more rows(dados <- left_join(tenSector, pwt) %>%
filter(Sector != "SmosGDP") %>% # retirando o agregado
mutate(VA = VA/PPP) %>%
select(-PPP) %>%
group_by(Year, Country) %>%
mutate(totVA = sum(VA, na.rm = TRUE),
totEMP = sum(EMP, na.rm = TRUE),
VAperCapitaAgg = totVA / totEMP) %>% # valor adicionado per capita AGREGADO
ungroup() %>%
mutate(empShare = EMP / totEMP,
vaShare = VA / totVA,
VAperCapita = VA / EMP, # VA per capita do setor
perCapitaShare = empShare*VAperCapita / VAperCapitaAgg) # partilha no VA per capita agregado do setor
) ## # A tibble: 25,350 x 13
## Country Region Year Sector EMP VA totVA totEMP VAperCapitaAgg
## <chr> <chr> <dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 ARG Latin… 1950 Agrcl… 1.80e6 1.36e10 1.15e11 6.54e6 17640.
## 2 ARG Latin… 1950 Cm,sa… 4.11e5 5.89e 9 1.15e11 6.54e6 17640.
## 3 ARG Latin… 1950 Cnstr… 3.14e5 7.70e 9 1.15e11 6.54e6 17640.
## 4 ARG Latin… 1950 Firea… 2.04e5 5.34e 9 1.15e11 6.54e6 17640.
## 5 ARG Latin… 1950 Gvrnm… 8.25e5 2.00e10 1.15e11 6.54e6 17640.
## 6 ARG Latin… 1950 Mnfct… 1.60e6 3.39e10 1.15e11 6.54e6 17640.
## 7 ARG Latin… 1950 Mining 3.27e4 1.67e 9 1.15e11 6.54e6 17640.
## 8 ARG Latin… 1950 Trd,r… 8.90e5 2.05e10 1.15e11 6.54e6 17640.
## 9 ARG Latin… 1950 Trn,s… 4.25e5 6.34e 9 1.15e11 6.54e6 17640.
## 10 ARG Latin… 1950 Utili… 3.93e4 4.82e 8 1.15e11 6.54e6 17640.
## # … with 25,340 more rows, and 4 more variables: empShare <dbl>, vaShare <dbl>,
## # VAperCapita <dbl>, perCapitaShare <dbl>Com dados em mãos podemos plotar verdadeiras cenas de horror. Atenção, cenas fortes seguirão. Leitores viúvas do regime militar podem ficar abalados:
dados %>%
filter(Country %in% c("BRA", "KOR"), Sector == "Mnfctrn") %>%
ggplot(aes(x = Year, y = empShare, color = Country)) +
geom_line(size = 1.2) +
labs(x = "Ano",
y = "% da for?a de trabalho na Manufatura",
color = "Pa?s") +
scale_y_continuous(labels = scales::percent) +
theme_minimal()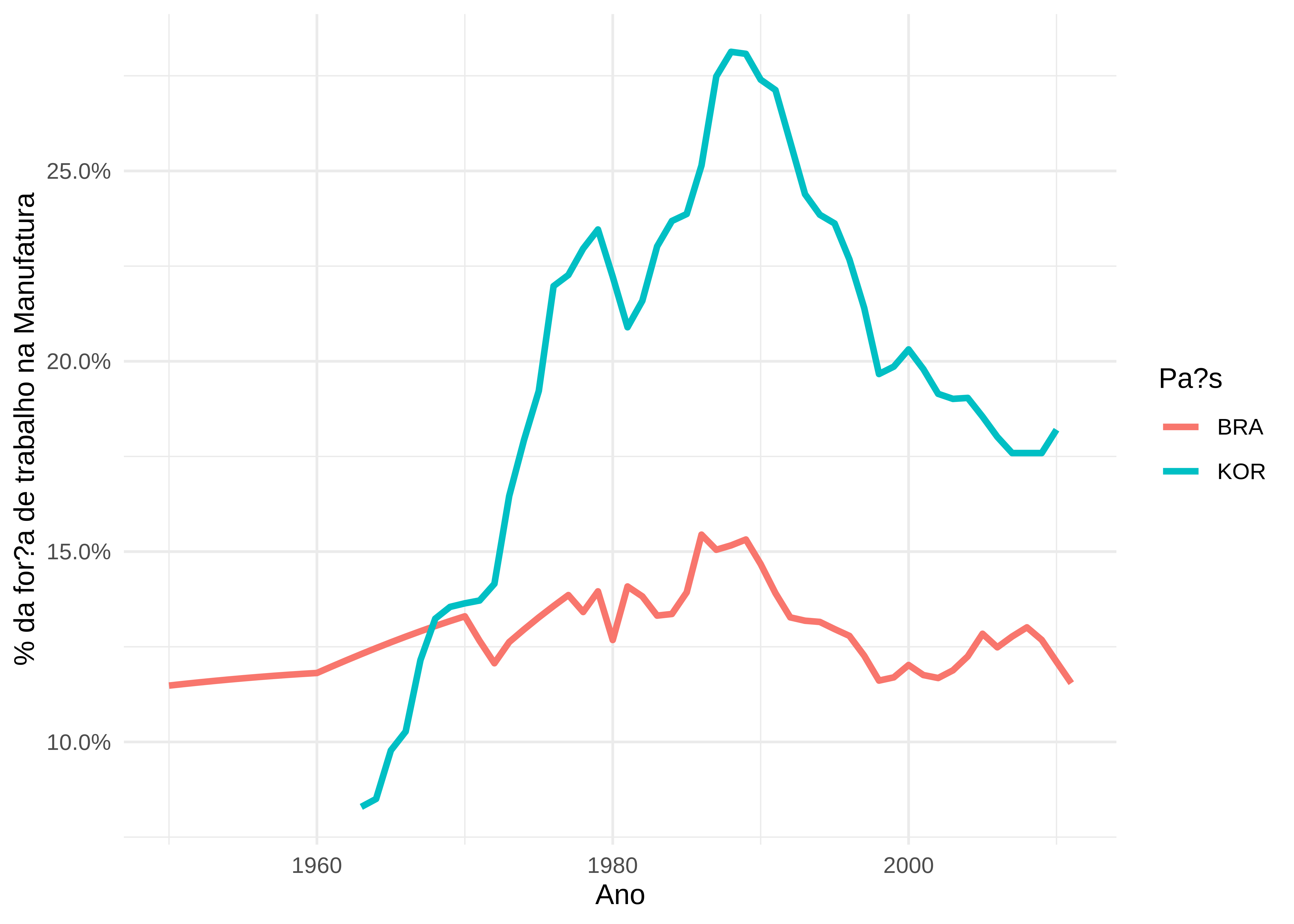
Piadinhas à parte, vamos fazer um experimento? Tomar a Coréia do Sul de 2005 (limitações de dados da base, eu queria ter algo detalhado assim mais recente), manter a produtividade de cada setor igual, mas deixar a distribuição do trabalho igual à do Brasil, um país menos industrializado. O que acontece com a renda per capita?
Primeiro eu vou abstrair a operação em uma função:
contrafactual <- function(.data, country1, country2, year = 2005, type) {
country1 <- .data %>%
filter(Country == country1, Year == year) %>%
select(Year, empShare, Sector, VAperCapita) %>%
rename(empShare1 = empShare,
VAperCapita1 = VAperCapita)
country2 <- .data %>%
filter(Country == country2, Year == year) %>%
select(Year, Sector, VAperCapitaAgg, VAperCapita, empShare) %>%
left_join(country1)
if(type == "structure") {
country2 %>%
group_by(VAperCapitaAgg) %>%
summarise(contrafactual = sum(VAperCapita*empShare1, na.rm = TRUE)) %>%
mutate(type = "Structure",
var = contrafactual - VAperCapitaAgg,
varPerc = var/VAperCapitaAgg) %>%
return()
} else {
country2 %>%
group_by(VAperCapitaAgg) %>%
summarise(contrafactual = sum(VAperCapita1*empShare, na.rm = TRUE)) %>%
mutate(type = "Productivity",
var = contrafactual - VAperCapitaAgg,
varPerc = var/VAperCapitaAgg) %>%
return()
}
}Agora vemos os dois cenários. O primeiro, em que a Coréia do Sul mantém sua produtividade em cada setor, mas vira uma economia menos industrializada. O segundo, em que mantém sua estrutura produtiva atual, mas ganha em cada setor a produtividade brasileira naquele setor.
bind_rows(contrafactual(dados, "BRA", "KOR", type = "structure"),
contrafactual(dados, "BRA", "KOR", type = "productivity"))## # A tibble: 2 x 5
## VAperCapitaAgg contrafactual type var varPerc
## <dbl> <dbl> <chr> <dbl> <dbl>
## 1 44329. 35861. Structure -8468. -0.191
## 2 44329. 13553. Productivity -30776. -0.694Note que desindustrializar tomou um custo em termos de valor adicionado de um trabalhador médio, mas nada perto da destruição que foi adquirir a produtividade brasileira em todos os setores. E se invertermos o exercício?
bind_rows(contrafactual(dados, "KOR", "BRA", type = "structure"),
contrafactual(dados, "KOR", "BRA", type = "productivity"))## # A tibble: 2 x 5
## VAperCapitaAgg contrafactual type var varPerc
## <dbl> <dbl> <chr> <dbl> <dbl>
## 1 13864. 13553. Structure -311. -0.0224
## 2 13864. 35861. Productivity 21997. 1.59Manter a produtividade em cada setor como está, porém industrializar rapidamente leva a uma queda pequena no valor adicionado per capita. Agora, manter a estrutura produtiva exatamente como está, porém adquirindo a produtividade coreana em cada setor, nosso valor adicionado médio sobe ~.