Hamiltonian Monte Carlo

Nota: por um typo esse post saiu no blog antes de ficar completo, infelizmente. Essa versão conta com correções e bibliografia

No milênio passado (ou seja, antes de maio), eu falei sobre MCMC, que é um método muito usado pela galera de bayesiana para amostrar a posterior de uma distribuição. O Random Walk Metropolis Hasting (RWMH), o algoritmo que eu apresentei naquele post, sempre me causou sentimentos contraditórios: a correção para amostrar a distribuição é simples e muito esperta. O Random Walk sempre me soou particularmente problemático. Sim, ele é necessário para garantir que a convergência da distribuição ocorre para a distribuição certa. Sim, ele é super simples, é só um random walk. Mas a ideia de sair por ai passeando no espaço de parâmetros e finalmente esbarrar no lugar certo parece um tanto o quanto ruim. A taxa de rejeição do RWMH também sempre me causou arrepios: a taxa ótima de aceitação se a dimensão do espaço de parâmetros é maior do que 5 é de 23%. Ou seja, a cada 3 passos que você dá, menos de um é aceito.

Bayesianos: Não me levem a mal. Tudo isso é muito bem construído de maneira que você obtém a distribuição correta no final, e funciona muito bem! Eu só não gosto do Random Walk.

Felizmente eu não sou o único com problemas com o Random Walk na proposta, e em 1996 apareceu um uso (em estatística) de um algoritmo que evita o random walk justamente por ele ser ineficiente, especialmente em alta dimensão. O nome é Hamiltonian Monte Carlo (originalmente, Hybrid Monte Carlo). A ideia é bem esperta e felizmente já tem uma dúzia de implementações: a mais robusta e bem trabalhada é o stan.

A ideia: no lugar de um random walk, nós usamos o gradiente da distribuição para nos informar aonde ir. Veja que a maioria das distribuições bem comportadas tem muita massa perto do máximo, então se a gente mapear perto do máximo nós vamos mapear um bom pedaço da distribuição. Obviamente, se nós seguirmos o gradiente nós vamos achar o máximo. Nosso objetivo não é encontrar o máximo e sim mapear a distribuição. O truque é converter o gradiente em algo que informe a gente como passear na distribuição.

Veja que a ideia de passear ao redor da distribuição de maneira estável quando tem um ponto que atrai a partícula é análogo a um foguete entrar em órbita: o planeta vai tentar te puxar para baixo, e o seu objetivo é não cair. Assim como um foguete, nosso algoritmo pode passear se tiver impulso o suficiente. O Hamiltoniano é uma maneira de formalizar isso. Nós não temos nada naturalmente similar a um impulso na hora de amostrar uma distribuição, então vamos ter que inventar um. Em tempo, o Hamilton do Hamiltoniano não é o mesmo do musical.

O passo a passo:

1. Amostre um valor para o momento
2. Simule a dinâmica do sistema
3. Faça um aceita-rejeita Metropolis Hasting

O diabo está nos detalhes: A gente tem que se preocupar em simular a dinâmica. Felizmente a dinâmica é bem simples: estamos no espaço (sideral), então não há atrito. Nós temos um momento (no sentido físico) e ele vai ser atualizado conforme o campo gravitacional - o gradiente. Mas, a simulação tem que ser estável suficiente para o erro numérico não dominar rapidamente. A boa notícia é que tem um algoritmo super simples para fazer isso, o leapfrog integrator. Basicamente, dentro de um loop (Pedro provavelmente vai ficar insatisfeito com isso), faça:

1. Atualize o valor do momento \(\phi\), para \(\phi = \phi + 1/2\epsilon\bigtriangledown\mathcal{P}\), onde \(\mathcal{P}\) é a posterior, \(\bigtriangledown \mathcal{P}\) é o gradiente de \(\mathcal{P}\) e \(\epsilon\) é um hiperparâmetro
2. Atualize o valor dos parâmetros \(\theta = \theta + \epsilon M\phi\), onde \(M\) é uma matriz de hiperparâmetros
3. Atualize o valor do momento \(\phi\), para \(\phi = \phi + 1/2\epsilon\bigtriangledown\mathcal{P}\)

Noutras palavras, dê meio passo no momento, veja a sua posição e dê mais meio passo. Talvez seja excesso de zelo, mas: para cada parâmetro nós temos um momento, então se temos \(p\) parâmetros, \(\phi\) é um vetor de dimensão \(p\).

Um leapfrog integrator tem a seguinte cara - eu vou implementar tudo em Julia por motivos que já já vão ficar claros:

mom_dist = MvNormal(M)

psi = rand(mom_dist)
for i = 1:L
        psi = psi + 1/2*leap_step*grad(new_par)
        new_par = new_par + inv(M)*leap_step*psi
        psi = psi + 1/2*leap_step*grad(new_par)
    end

Onde grad é o gradiente da nossa função alvo, i.e. a posterior. Veja que nós temos 3 hiperparâmetros que precisam ser definidos: \(L\), o número de etapas do leapfrog; \(\epsilon\) o tamanho de cada passo do leapfrog, também conhecido como stepsize; e \(M\), que é uma matriz de variância dos momentos. Para facilitar a vida, eu vou fazer \(\min(1/\epsilon,20)\), que é inspirado em uma sugestão do Bayesian Data Analysis. A matriz de variância dos momentos, no ótimo, deve ser a inversa da variância dos parâmetros. Em geral, as pessoas usam uma matriz diagonal e eu vou usar a diagonal da inversa da variância covariância dos parâmetros no ótimo (que eu calculei usando o Optim). Os momentos vão seguir uma Normal de média zero e matriz de covariância \(M\). Para escolher o tamanho de cada passo, \(\epsilon\), eu procedi usando a velha tentativa e erro para atingir o ótimo de aceitação do HMC, que é 65%: uma aceitação acima disso eu aumento o tamanho do stepsize; abaixo diso eu reduzo. O stepsize controla o quão longe nós vamos buscar a nova proposta de parâmetro.

Na etapa do metropolis hastings, nós aceitamos ou rejeitamos o conjunto de parâmetro e momento contra o momento e o parâmetro do começo da simulação. Se \(\phi\) e \(\theta\) são o momento e o parâmetro no início do algoritmo e \(\phi^*\) e \(\theta^*\) são o momento e o parâmetro depois dos passos do hamiltoniano, então nossa razão que vai para o Metropolis-Hasting:

\[\min\left\{1,\frac{\mathcal{P}(\theta^*|y)p(\phi^*)}{\mathcal{P}(\theta|y)p(\phi)}\right\}\]

O gradiente é essencial aqui, já que ele é computado a cada passo do leapfrog. Eu preciso dele computado rápido e precisamente. A melhor maneira de fazer isso é usando um procedimento chamado automatic differentiation, que tem várias implementações em Julia - enquanto isso, no R, a opção é justamente chamar o Julia para lidar com isso.

Um truque maravilhoso que eu vou usar é que, apesar de calibrar o \(\epsilon\), eu vou deixar o stepsize em cada passagem do algoritmo ser aleatório, centrado no valor que eu calibrei e com uma variância baixa. O problema de deixar \(\epsilon\) fixo é que em regiões com muita curvatura o stepsize que colocamos pode ser muito alto e a gente nunca aceitar nenhum ponto daquela região. Veja que alterar dinamicamente o tamanho do passo é complicado porque isso pode destruir a distribuição estacionária - o mesmo motivo para gente escolher os hiperparâmetros e jogar fora os parâmetros amostrados enquanto nós mudamos o algoritmo.

Para esse exemplo eu vou jogar um problema que tem 100 observações e 50 parâmetros. Eu vou colocar todas as priors com distribuição de Laplace, que tem a seguinte cara:

xx <- seq(-3,3,0.05)
yy <- dlaplace(xx)
df <- data.frame(x = xx,y=yy)

ggplot(df,aes(xx,yy)) + geom_line()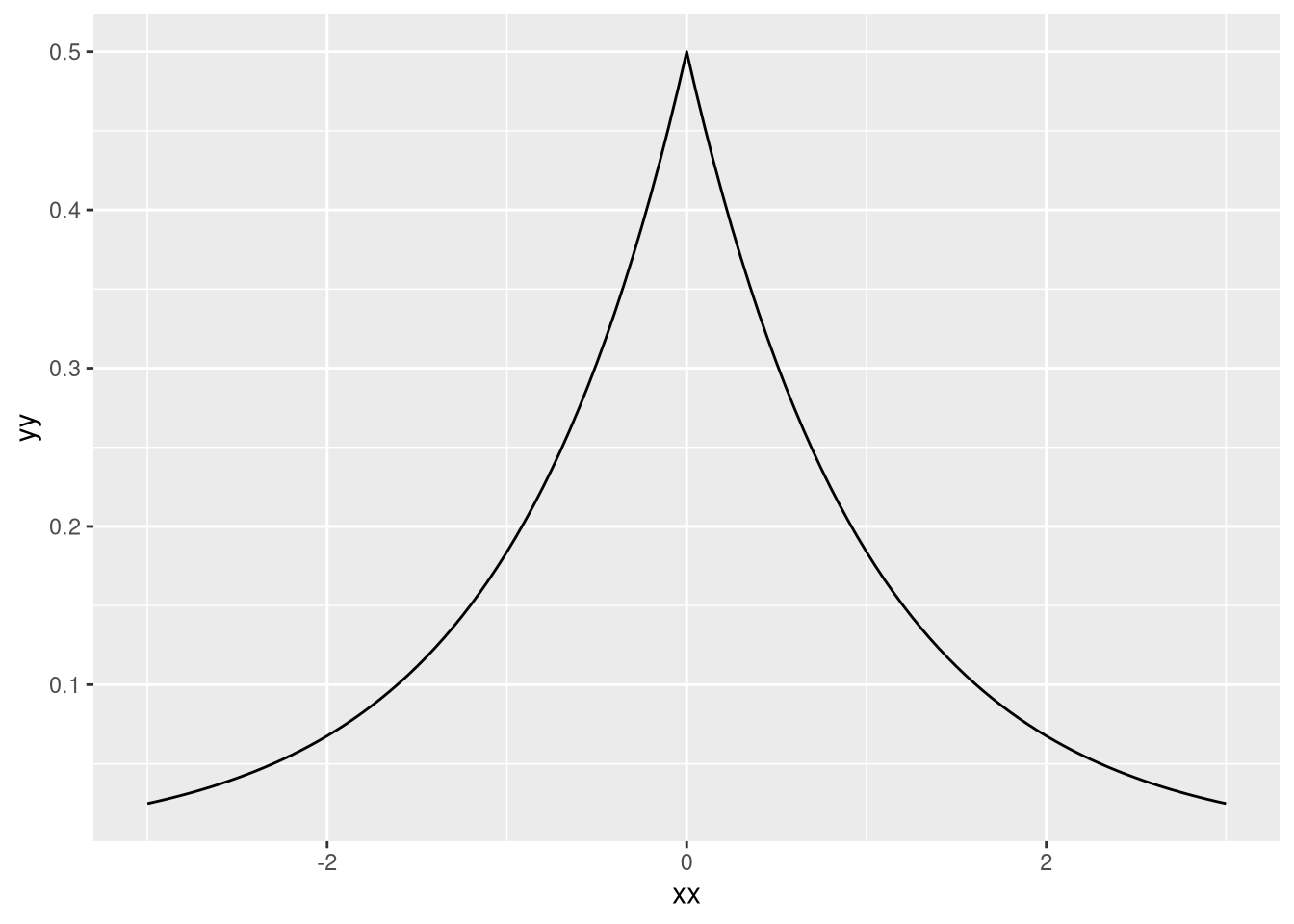 

(O dlaplace é do pacote extraDistr) A densidade dela é \(1/(2b)*exp(-|x-\mu|/b)\). Com uma verossimelhança normal, a posterior é exatamente o estimador do LASSO - fica como exercício para o leitor (dica: log). Vamos começar carregando os pacotes e criando as funções que precisamos:

using Distributions,StatsPlots, ForwardDiff, LinearAlgebra, PositiveFactorizations, Optim

n_samples = 2000

n = 100

x = randn(n,50)
theta = [repeat([1],10); repeat([0],40)]
y = x*theta + randn(n)

prior = Laplace(0,2)

ll(theta) = logpdf(MvNormal(I(n)),y-x*theta)

post(theta) = ll(theta) + sum(logpdf.(prior,theta))

init = rand(prior,50)

grad(theta) = ForwardDiff.gradient(post,theta)

O vetor de parâmetros verdadeiro é esparso e os dez primeiros valores são 1, todo o resto é 0. Eu vou procurar o máximo para obter a matriz de variância covariância dos parâmetros:

ot = optimize(x->-1*ll(x),zeros(50),BFGS(), autodiff=:forward)

M = grad(ot.minimizer)*grad(ot.minimizer)'#mass matrix
M = inv(diagm(diag(M)))

Veja que eu já garanti que a matriz é diagonal com diagm(diag()). Vamos definir a distribuição do momento:

mom_dist = MvNormal(M)

Agora, o momento depende do gradiente da função. Nós podemos gerar, propostas que jogam a gente em regiões que o gradiente é muito alto e isso vai envolver um valor da energia altíssimo. Usando nossa analogia física, seria equivalente a dar tanto impulso ao nosso foguete que ele vai dar um passeio no sistema solar. Uma coisa que gera isso são erros numéricos na simulação da trajetória. Para evitar isso, eu vou colocar um limite superior do momento. Mais alto que isso é sinal que tem alguma coisa profundamente errada na simulação.

tol_psi = 1e15

O setup básico: um array para receber os parâmetros, a distribuição uniforme entre 0 e 1 para decidir se aceita ou não na etapa do metropolis, o valor de \(\epsilon\), de L, um parâmetro para monitorar a aceitação e um chute inicial:

pars = zeros(n_samples,50)

uni = Uniform(0,1)

leap_step = 0.1

L = max(Int(ceil(1/leap_step)),20)

accept = 0

old_par = init#repeat([0],50)

leap_dist = Normal(leap_step,0.05)

Veja que a última linha cria uma distribuição centrada no valor de leap_step que sorteia aleatoriamente o tamanho do stepsize. Eu faço uns 500 passos para fazer fine tunning do stepsize e obter um ponto um pouquinho melhor que o chute inicial. Eu poderia usar o valor do ótimo que eu obtive otimização a máxima verossimelhança, mas eu não vou fazer:

for j = 1:n_samples
    psi = rand(mom_dist)
    old_psi = psi
    new_par = old_par
    for i = 1:L
        psi = psi + 1/2*leap_step*grad(new_par)
        new_par = new_par + inv(M)*leap_step*psi
        psi = psi + 1/2*leap_step*grad(new_par)
    end
    if any(psi .> tol_psi)
        @info "Energy diverging. Quitting"
        break
    end
    r = post(new_par) + logpdf(mom_dist,psi) - (post(old_par)+ logpdf(mom_dist,old_psi))
    a = rand(uni)
    r = min(1,exp(r))
    if r > a
        pars[j,:] = new_par
        global old_par = new_par
        global accept = accept + 1
    else
        pars[j,:] = old_par
    end
    println("Iteration ", j, " Accept ratio ", accept/j*100, "%")
end

Em portugês: o primeiro for implementa o leapfrog. Na linha seguinte nós checamos se a energia não divergiu - se sim, saímos imediatamente do loop e informamos ao usuário. Depois temos uma etapa de aceitação de Metropolis Hasting, parecido com o RWMH.

Como o exemplo tem 50 parâmetros, eu não vou fazer a maldade de colocar aqui os 50 gráficos das distribuições - mas eles estão no github. Só vou escolher alguns:

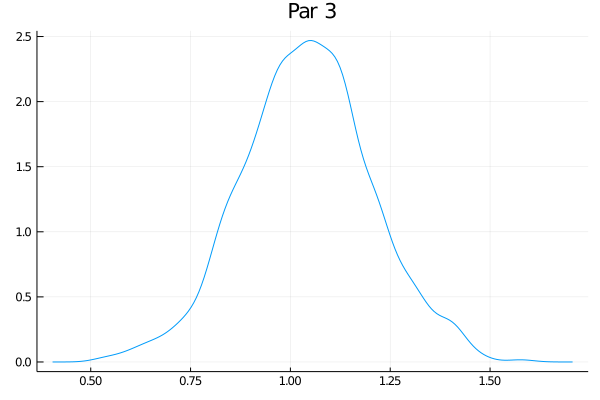
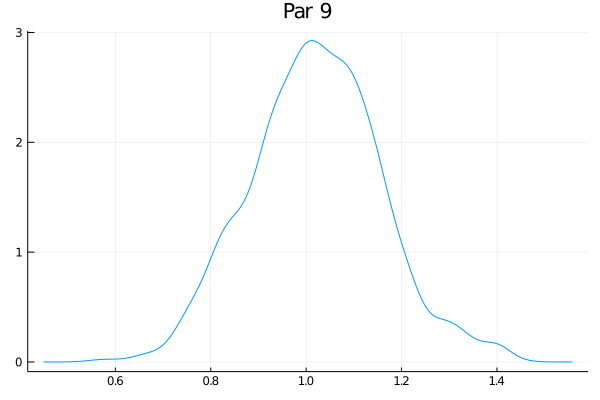
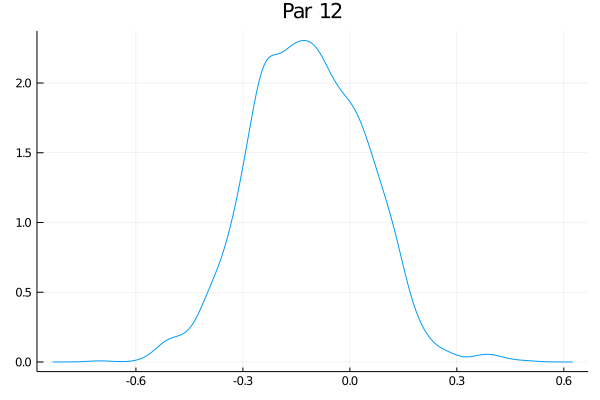
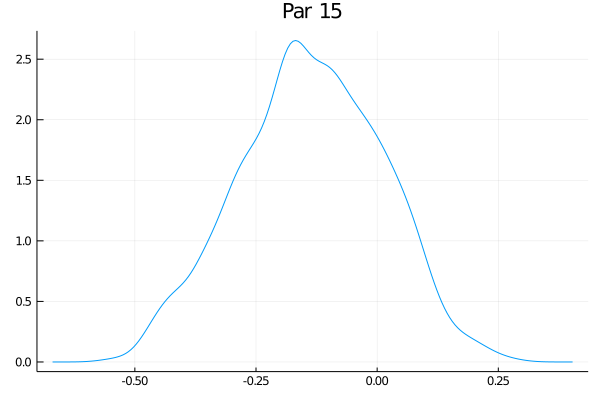
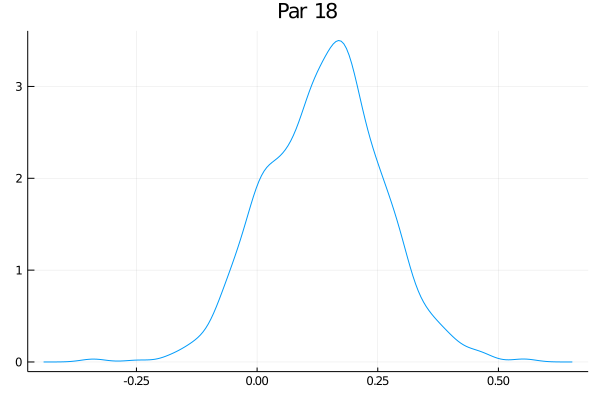
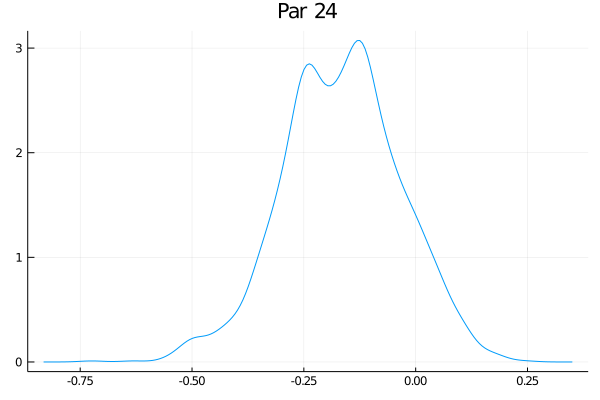
Eles não estão perfeitamente centrados nem super bonitos, mas funciona bastante bem. O último gráfico claramente tem um pequeno problema. Veja que nesse exemplo de brincadeira o RWMH usual deve funcionar bem, mas eu tenho as minhas dúvidas se um espaço com 500 parâmetros ia transmitir melhor as ideias (e meu computador ia sofrer um bocado).

O stan não usa esse algoritmo exatamente: ele usa uma variação do HMC chamado NUTS - No U Turns. A ideia em uma frase: toda vez que a gente começa a virar para voltar para o início da trajetória - um U turn - o algoritmo para. Fazer isso exatamente como eu escrevi destroi as propriedades da distribuição estacionária ser a distribuição alvo, então tem vários passos intermediários que implementam isso.