Remastered: Interpolação

Este é mais um post que já foi feito faz tempo, mas eu quero repetir mais pra mostrar um truque que eu aprendi, além de deixar a programação mais clara (com um pouco de sorte).

Imagina que você conhece a função em alguns pontos. A gente teve um exemplo disso no post passado de programação dinâmica: a gente calcula o valor da função valor ou da função política em alguns pontos. A interpolação garante que na hora de otimizar a gente vai poder visitar valores da função valor entre esses pontos.

O problema é como conectar esses pontos. Os que entre vocês já fizeram análise sabem que sempre podemos arranjar um polinômio “próximo” de uma função qualquer se o espaço é compacto. Se você tem n pontos, você poderia se sentir tentado a buscar um polinômio de ordem \(n-1\) que passe por todos os pontos.

Isso nem sempre é razoável e a função super inocente \(\frac{1}{1+10x^2}\) mostra porque não. Primeiro, vamos dar uma olhada nela:

using Plots; #isso carrega o pacote plots

grid2 =  range(-1,1,length=50) #um grid de pontos para avaliar a função

f(x)=(1+10*x^2)^(-1) #a função

plot(grid2,f.(grid2))

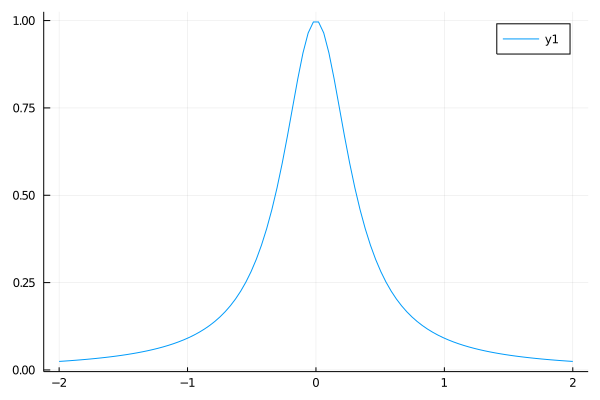
É uma função não muito maluca. Eu vou usar o pacote polynomials pra gerar um polinômio de grau 50, a partir de 50 pontos equiespaçados:

using Polynomials #o pacote polynomials tem uma função fit que busca o polinômio que passa por todos os pontos

grid =  range(-2,2,length=10) #um grid de pontos para avaliar a função

f_hat = fit(grid,f.(grid)) #isso vai gerar um polinômio que passa por todos os pontos - ele retorna uma função, então você pode passar pontos e obter os valores da função de volta em qualquer ponto

plot(grid2,f.(grid2))
plot!(grid2,f_hat.(grid2))

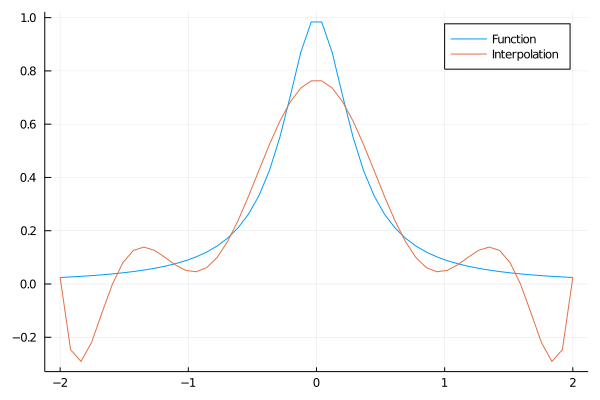
A interpolação gera uma função que oscila malucamente entre os pontos. O mais curioso é que aumentar o número de pontos piora a situação. Com 50 pontos:

f_hat = Polynomials.fit(grid2,f.(grid2))

plot(grid2,f.(grid2))
plot!(grid2,f_hat.(grid2))

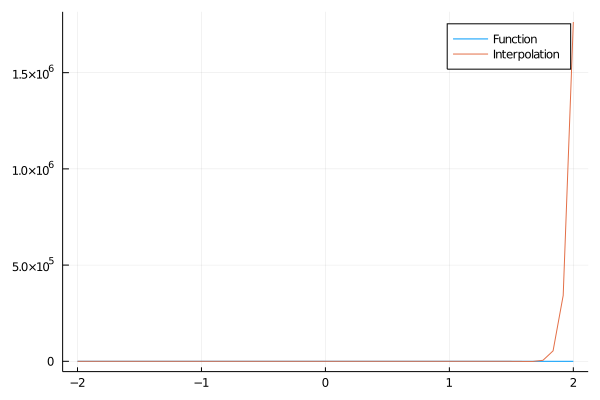
Isso serve como exemplo de como interpolações podem dar profundamente erradas. Nós estamos acostumados a pensar em overfitting quando a gente extrapola os dados, mas mesmo interpolações podem ser “do mal”. A interpolação claramente está fazendo um overfitting: nos pontos observados a aproximação é exata, mas fora deles é completamente maluco.

No post original eu sugeria fazer interpolação por pedaços, ligando cada pedaço por uma reta: eu vou usar o pacote Interpolations e o comando LinearInterpolation pra isso:

using Interpolations

lin_interp = LinearInterpolation(grid,f.(grid)) #gera uma interpolação linear, e retorna uma função

plot(grid2,f.(grid2))
plot!(grid2,lin_interp.(grid2))

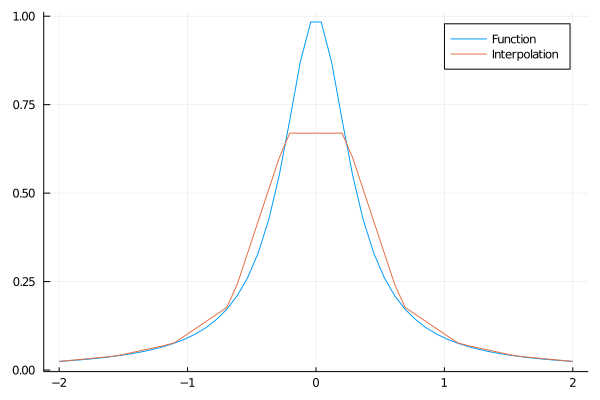
Veja que ficou bem feio porque tem só 10 pedaços. Com mais pedaços a interpolação fica indistinguível da função verdadeira:

grid3 = range(-2,2,length = 100)

lin_interp = LinearInterpolation(grid2,f.(grid2))

plot(grid3,f.(grid3))
plot!(grid3,lin_interp.(grid3))

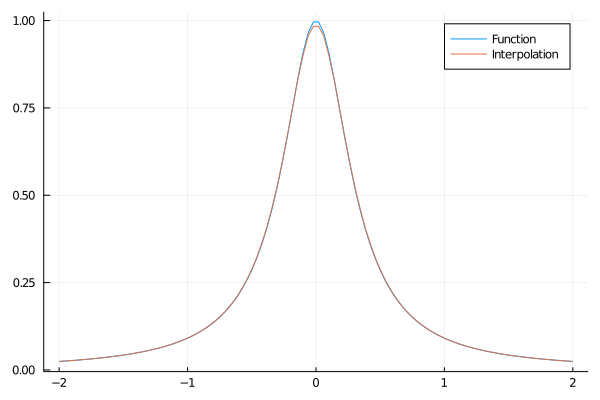
Você pode conectar os pontos por coisas que não são lineares - por exemplo, polinômios. Usar polinômios tem a vantagem que as derivadas de ordem mais alta existem - splines fazem isso e evitam o problema de oscilarem malucamente.

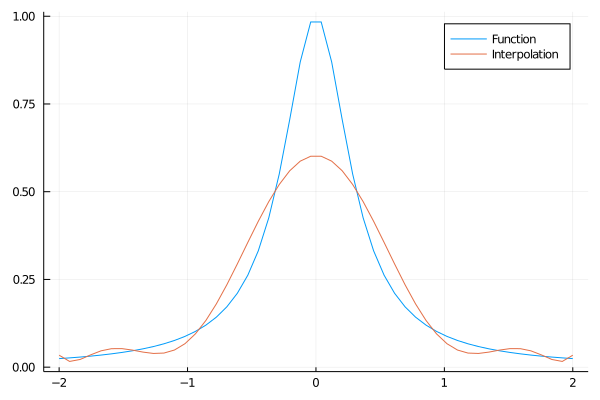
Mas mais interessante é que o grande problema aqui não é simplesmente o método de interpolação: é como o grid é gerado. Via de regra o grid é gerado com pontos equiespaçados - que é a maneira mais normal de pensar no problema. A gente não precisa necessariamente gerar pontos assim. Uma maneira totalmente maluca de gerar \(m\) pontos é:

\[x_k = -\cos\left(\frac{2k-1}{2m}\pi\right) \quad k =1, \ldots,m \]

Que gera pontos entre \([-1,1]\). Esse grid se deve ao Chebyschev. Veja que podemos pensar em maneiras de mover e encolher/crescer o intervalo para ficar entre \([a,b]\). Vamos criar uma função que pega uma sequência de pontos e gera o grid:

function cheby_nod(seq)
    m = length(seq)
     return map(k->-cos((2k-1)/(2m)*pi),seq)
 end

Escrevendo o post eu me dei conta que era mais simples passar \(m\) e criar a sequência depois. Eu podia muito bem ter usado um for, mas o map é brutalmente mais conciso. Vamos ver a qualidade da interpolação:

new_grid = 2*cheby_nod(1:10)

fit_cheb = Polynomials.fit(new_grid,f.(new_grid))

plot(grid2,f.(grid2))
plot!(grid2,fit_cheb.(grid2))

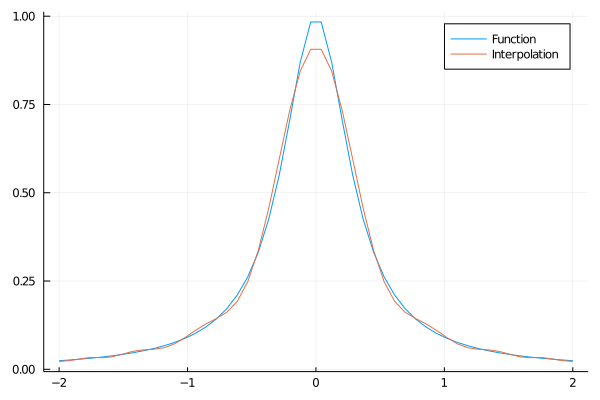
A coisa realmente legal aqui é que aumentar a quantidade de pontos melhora a qualidade da interpolação:

new_grid = 2*cheby_nod(1:20)

fit_cheb = Polynomials.fit(new_grid,f.(new_grid))

plot(grid2,f.(grid2))
plot!(grid2,fit_cheb.(grid2))

Eu nunca pensaria que gerar um grid usando cosseno seria uma boa ideia!

Alguns de vocês podem ter notado que eu gerei dois grids, um para gerar a interpolação e outro para avaliar a interpolação. Se vocês ainda não sacaram, o plot é gerado conectando os pontos por segmentos de reta, então se eu fizesse o gráfico da função original com o grid da interpolação os dois iam ser indistinguíveis.

Este post basicamente deve a sua existência ao Numerical Methods in Economics do Kenneth Judd - aparentemente uma segunda edição sairá em breve.