Mais raízes unitárias

O Pedro já fez um post sobre regressão espúria, que vai direto ao ponto. Mas faz muito tempo (2019) e recentemente isso voltou a moda eu decidi escrever sobre isso.

O post do Pedro comete um pequeno deslize, que é fazer as coisas com uma tendência determinística. Algumas pessoas podem argumentar que “isso não é exatamente uma regressão espúria”: uma regressão espúria é o caso em que nós temos dois processos com raízes unitárias¹! Mais importante, eu acho mais incrível o caso em que não existe nenhuma tendência determinística.

Eu vou fazer uma simulação absolutamente simples, de dois random walks, e vou regredir um no outro. O random walk é um processo fascinante e extremamente simples:

\[ x_t = x_{t-1} + \epsilon_t \]

Onde \(\epsilon_t\) é um choque normal com média zero e variância 1. A primeira coisa a se atentar é que \(x_t\) pode ser escrito como uma soma dos choques:

\[ x_t = \sum_{j=0}^t \epsilon_j \]

Voltando a simulação: a função que vai fazer todo o trabalho só recebe o tamanho da série a ser gerada e gera duas séries de números saídos da normal e gera dois random walks. Por último, ela regride um random walk no outro:

library(ggplot2)
library(purrr)
library(BETS)

## Registered S3 method overwritten by 'quantmod':
##   method            from
##   as.zoo.data.frame zoo

## 
## Attaching package: 'BETS'

## The following object is masked from 'package:stats':
## 
##     predict

library(urca)
library(zoo)

## 
## Attaching package: 'zoo'

## The following objects are masked from 'package:base':
## 
##     as.Date, as.Date.numeric

set.seed(202106)

testa_rw <- function(n){
  
  x <- cumsum(rnorm(n))
  y <- cumsum(rnorm(n))
  
  reg <- lm(y ~ x)
  
  return(reg)
  
}

A simulação:

lista <- replicate(2000,1000,simplify = FALSE)

resultados <- map(lista,testa_rw)

O resultados tem várias coisas legais. Por exemplo, como é a distribuição da estatística t? A nossa intuição manda que dois processos independentes, o coeficiente da estatística \(t\) seja baixo. Mas:

t_stat <- map_dbl(resultados,~(summary(.)$coefficients[2,3]))

ggplot(data.frame(t_stat = t_stat),aes(t_stat)) + geom_histogram() + theme_minimal()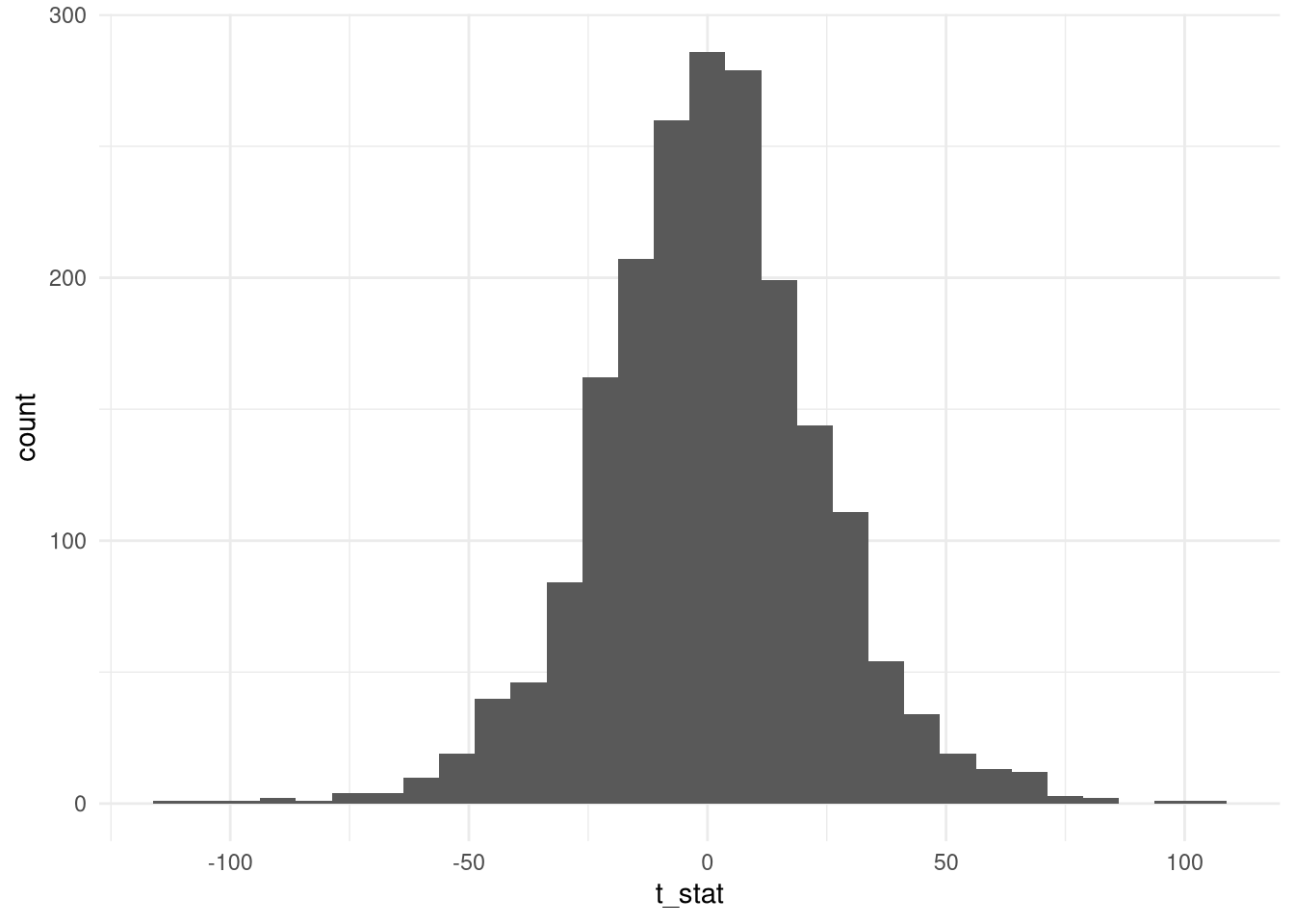

A imagem pode dar uma enganada: observe o eixo x. Os valores variam entre -100 e 100! Qual a proporção de casos que estão acima de 2 (em módulo)?

acima2 <- abs(t_stat) > 2

mean(acima2)

## [1] 0.923

Sim, mais de 90% dos casos estão acima de 2.

Veja que, ao contrário do post do Pedro, aqui não tem nenhuma tendência. Os processos são puramente random walks gerados independentemente.

Só porque eu quero martelar esse ponto, eu vou mostrar o histograma das correlações:

teste_rw <- function(n){
  
  x <- cumsum(rnorm(n))
  y <- cumsum(rnorm(n))
  
  return(cor(x,y))
}

resultados2 <- map_dbl(lista,teste_rw)

ggplot(data.frame(cor = resultados2),aes(cor)) + geom_histogram() + theme_minimal()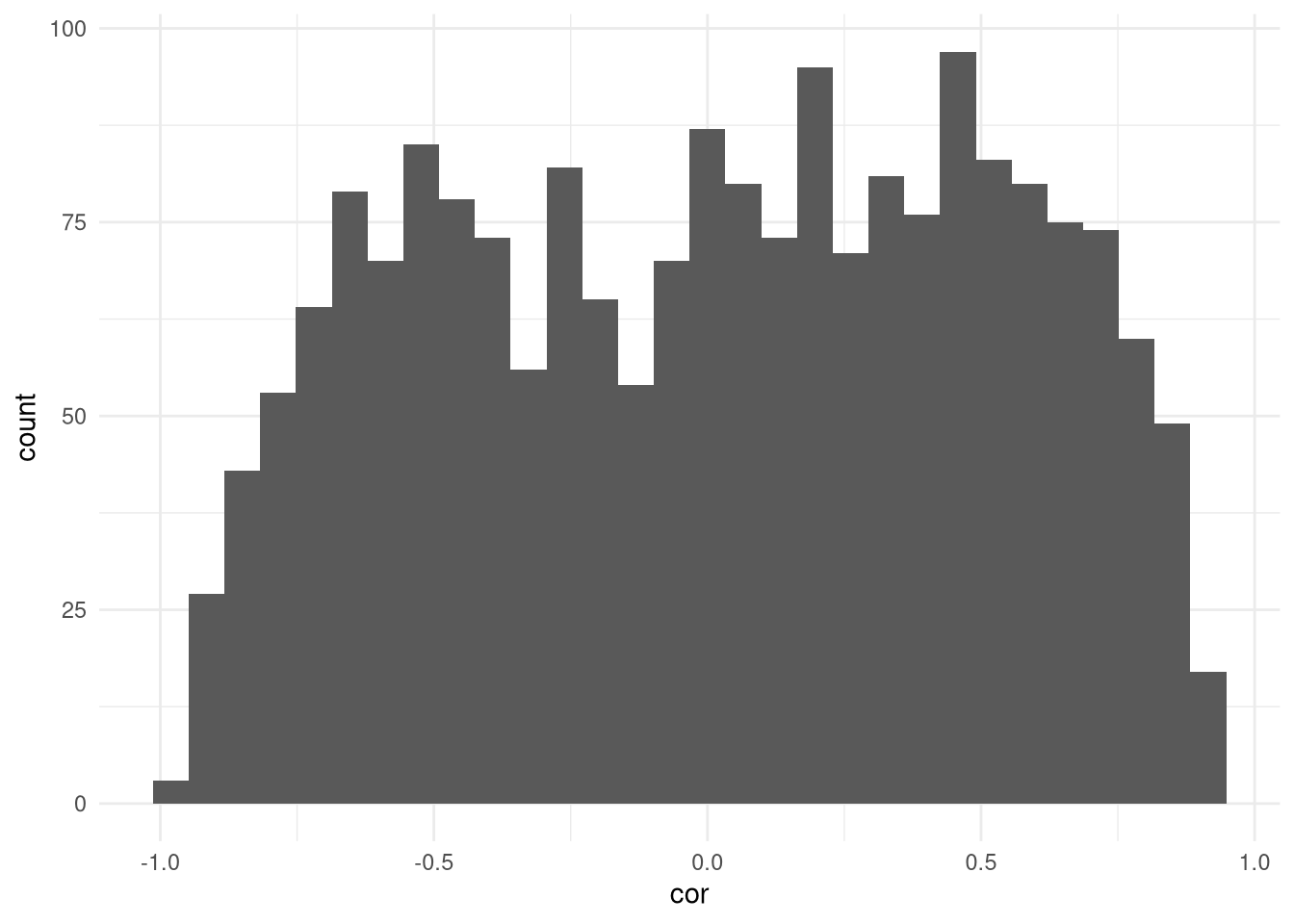

Portanto, proceder no caso de raiz unitária com regressões pode levar a resultados extremamente inesperados. Para entender parte do problema, relembre como a gente escreveu o random walk:

\[ x_t = \sum_{j=1}^t \epsilon_j \] Lembre que os \(\epsilon_j\) são independentes, e considere \(t \rightarrow \infty\). A variância do processo estoura para infinito.

Eu quero adicionar que, como humilhação pouca é bobagem, testes de raiz unitária são notoriamente problemáticos (sofrem baixo poder), o que compõe o problema. É difícil separar uma série não estacionária de uma série estacionária extremamente persistente.

Para ter um exemplo empírico, vamos olhar uma série que eu achava que era não estacionária: o câmbio.

cambio <- BETSget(1)

cambio_ts <- zoo(cambio$value,cambio$date)

Eu vou pegar a partir de 2004 porque isso evita o período do Lula. Isso não é uma escolha sem efeitos colaterais: eu preferiria uma série mais longa para testar. Mais ainda, se eu estou eliminando o ruído do Lula I, então porque não focar até antes de 2008, para evitar a crise? Ai eu teria uma série curta demais:

cambio_ts <- window(cambio_ts, start = as.Date("2004-01-01"))

ggplot(data.frame(data = time(cambio_ts),cambio = cambio_ts),aes(data,cambio)) + geom_line() + theme_minimal()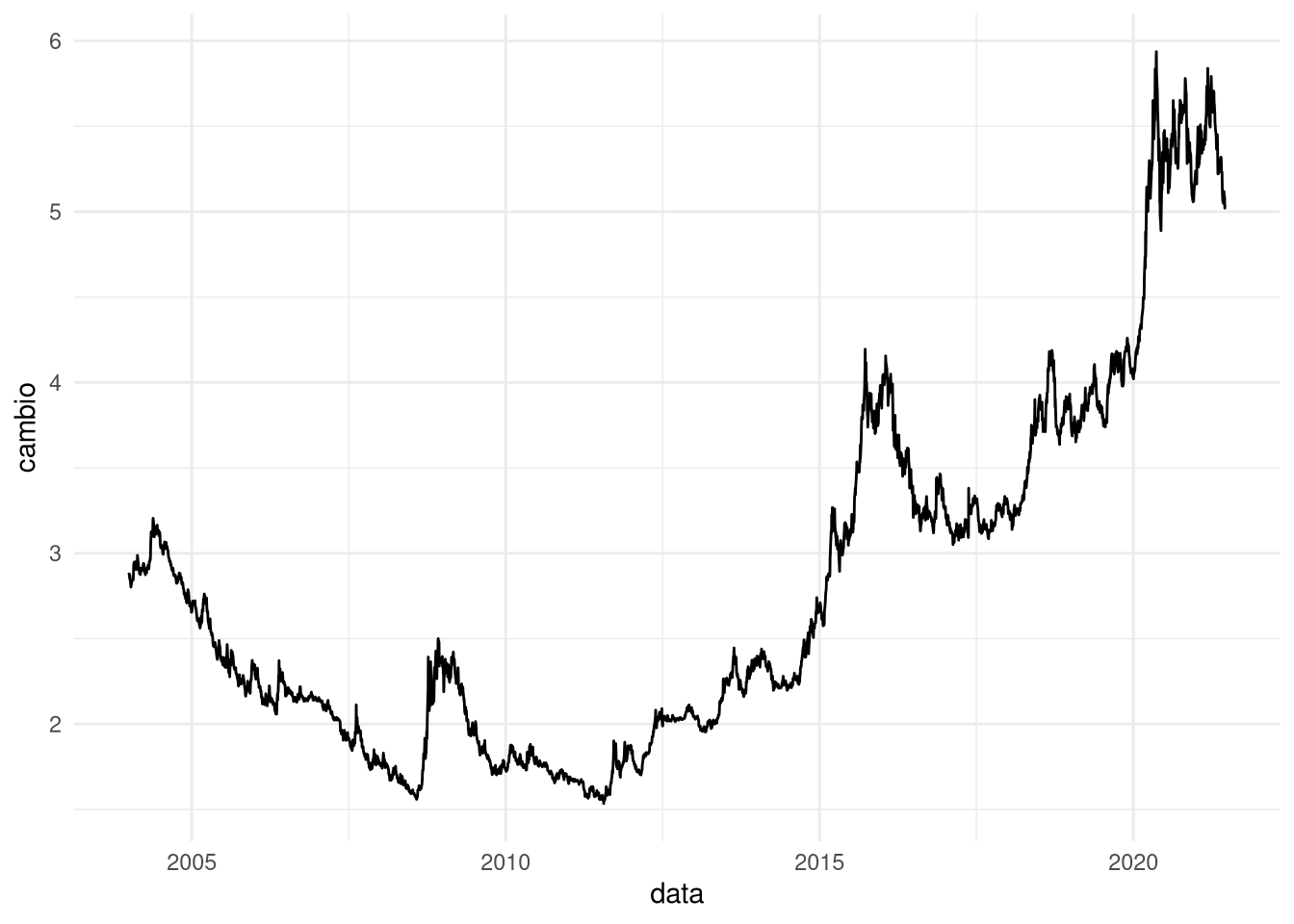

Eu acho a série gritantemente não estacionária. Vamos fazer o teste ADF:

summary(ur.df(cambio_ts))

## 
## ############################################### 
## # Augmented Dickey-Fuller Test Unit Root Test # 
## ############################################### 
## 
## Test regression none 
## 
## 
## Call:
## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.249548 -0.012298 -0.000674  0.011161  0.272278 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## z.lag.1    0.0001646  0.0001541   1.068    0.286
## z.diff.lag 0.0204572  0.0151091   1.354    0.176
## 
## Residual standard error: 0.03024 on 4380 degrees of freedom
## Multiple R-squared:  0.0006966,  Adjusted R-squared:  0.0002403 
## F-statistic: 1.527 on 2 and 4380 DF,  p-value: 0.2174
## 
## 
## Value of test-statistic is: 1.0679 
## 
## Critical values for test statistics: 
##       1pct  5pct 10pct
## tau1 -2.58 -1.95 -1.62

(Sim, um lag é suficiente) O teste rejeita a hipótese de estacionariedade.

Só porque eu quero matar uma possível crítica: o que acontece se eu excluir o período Bolsonaro?

cambio_ts2 <- window(cambio_ts, end= as.Date("2018-12-31"))

ggplot(data.frame(data = time(cambio_ts2),cambio = cambio_ts2),aes(data,cambio)) + geom_line() + theme_minimal()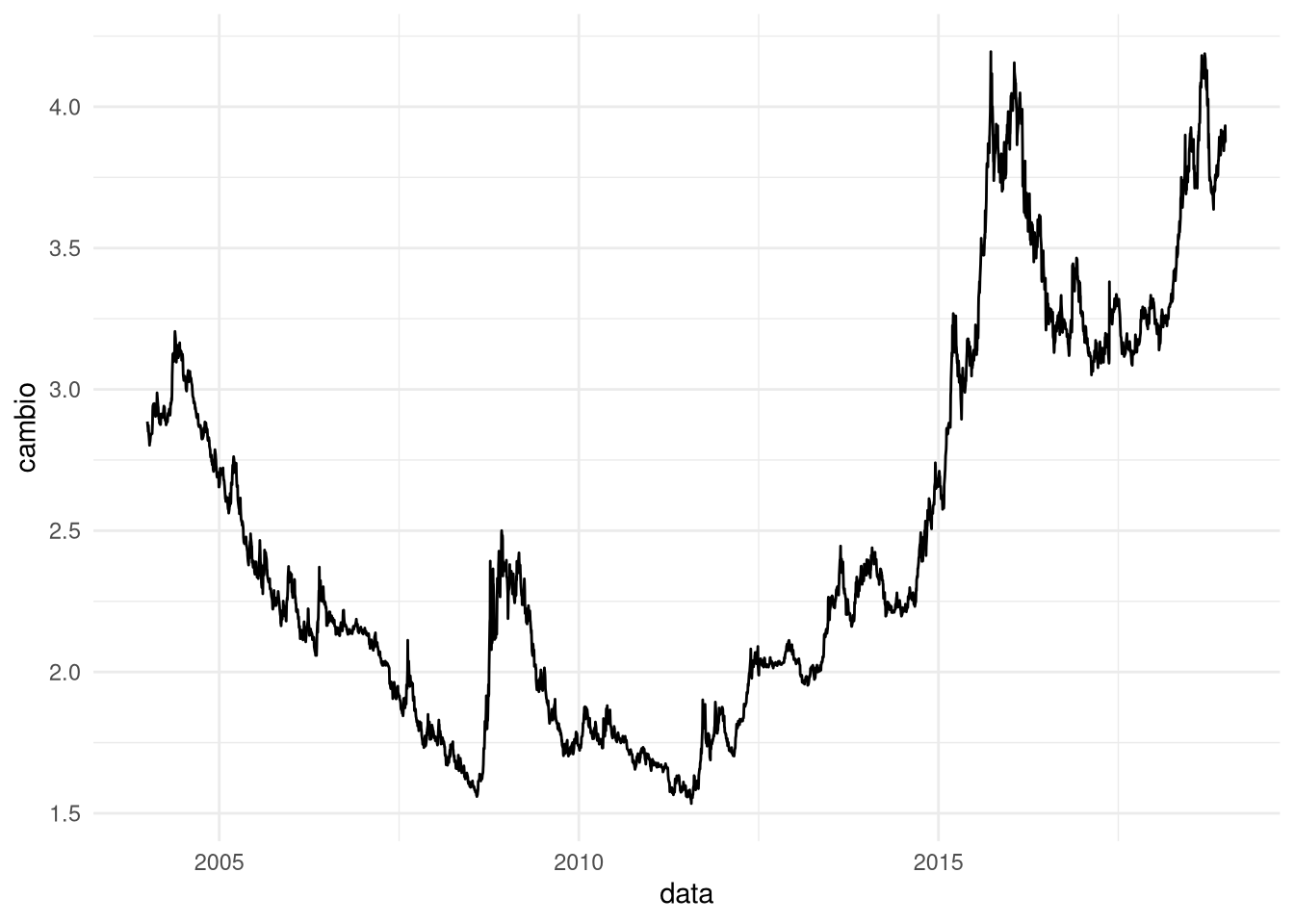

Isso retira o pedaço final da série em que a taxa de câmbio se desvaloriza. De repente é essa mudança, e não nenhuma coisa de não estacionariedade, que leva o teste a apontar uma raiz unitária:

summary(ur.df(cambio_ts2))

## 
## ############################################### 
## # Augmented Dickey-Fuller Test Unit Root Test # 
## ############################################### 
## 
## Test regression none 
## 
## 
## Call:
## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.247073 -0.011132 -0.000630  0.009905  0.272865 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)
## z.lag.1     0.0000927  0.0001584   0.585    0.558
## z.diff.lag -0.0034790  0.0163062  -0.213    0.831
## 
## Residual standard error: 0.02478 on 3761 degrees of freedom
## Multiple R-squared:  0.0001019,  Adjusted R-squared:  -0.0004298 
## F-statistic: 0.1917 on 2 and 3761 DF,  p-value: 0.8256
## 
## 
## Value of test-statistic is: 0.5852 
## 
## Critical values for test statistics: 
##       1pct  5pct 10pct
## tau1 -2.58 -1.95 -1.62

A estatística do teste cai um pouco, mas não corre nenhum risco de a gente rejeitar a hipótese nula aos níveis usuais de significância. A gente pode cortar mais ainda a série, mas em geral taxa de câmbio não é estacionária - e isso não é só pro Brasil.

Não estacionariedade é um tema fascinante e que apresenta várias armadilhas para quem trabalha com séries temporais.