Concentração do Máximo

Este post é uma continuação do post sobre concentração de medida, e vai ser necessário para um post futuro.

Naquele post eu falei sobre variáveis subgaussianas, para as quais a seguinte desigualdade vale:

$$P(|X| > t) \leq e^{-\frac{t^2}{2\sigma^2}}$$

Agora suponha que você tem uma coleção de variáveis aleatórias, todas subgaussianas e não necessariamente independentes. Neste post, nós vamos cotar a probabilidade do máximo delas ser maior que um valor t.

Se você precisa de uma motivação pra isso, eu ofereço duas:

1. Nós frequentemente trabalhamos com estimadores que minimizam ou maximizam alguma função: mínimos quadrados, máxima verossimelhança. É natural que estes estimadores dependam do máximo de uma variável aleatória
2. Se você está trabalhando com algum processo aleatório, muitas vezes o máximo pode ser mortal: qual é o máximo que um ativo pode perder se a distribuição dos retornos é subgaussiana, por exemplo?

O próximo post vai ilustrar uma aplicação dessas desigualdades no caso 1. Para o problema em mãos, nós queremos:

$$P\left(\max_{i=1,\ldots,n} |X| > t\right) \leq \text{?}$$

A primeira observação é que se o máximo de uma coleção é maior que $t$, então pelo menos um dos elementos da coleção é maior que $t$ (duhhh). Logo, o problema $\max_{i=1,\ldots,n} |X| > t$ é equivalente ao problema “pelo menos um dos $|X_i|$ é maior que t”. A gente vai escrever isso como $\bigcup_{i=1,\ldots,n} |X_i| > t$.

Qual a vantagem disso? Bom, a seguinte desigualdade vale:

$$P\left(\bigcup_{i=1,\ldots,n} |X_i| > t\right) \leq \sum_{i=1}^n P(|X_i| > t)$$

Eu não vou dar uma prova extremamente formal: se $A$ e $B$ são dijuntos - se $A$ acontece, então $B$ nunca acontece - então $P(A \cup B) = P(A) + P(B)$. Isso pode ser estendido pra qualquer união finita de conjuntos. Suponha o caso mais geral, em que $A$ e $B$ não são dijuntos. Eu posso escrever:

$$A \cup B = (A\cap B^c) \cup (A^c \cap B) \cup (A \cap B)$$

O superescrito $c$ significa o evento complementar. Pelo resto do post, $AB$ vai representar $A \cap B$. Veja que $A \cap B^c$ é dijunto de $A^c \cap B$ e os dois são dijuntos de $A \cap B$. Logo, eu escrevi a união de dois conjuntos como a união de dijuntos. Então:

$$P(A \cup B) = P(AB^c) + P(A^cB) + P(AB)$$

Agora, nós podemos escrever $A = AB^c \cup AB$ (A é a união de A interseção B e A interseção não B). Usando o único resultado que nós temos sobre probabilidade:

$$P(A) = P(AB) + P(AB^c) \therefore P(AB^c) = P(A) - P(AB)$$

Eu posso fazer a mesma coisa com $P(B)$, e nós temos:

$$P(A \cup B) = P(AB^c) + P(A^cB) + P(AB) = P(A) - P(AB) + P(B) - P(AB) + P(AB) = P(A) + P(B) - P(AB)$$

Agora, probabilidades são sempre não negativas, então:

$$P(A \cup B) = P(A) + P(B) - P(AB) \leq P(A) + P(B)$$

A nossa desigualdade é só é uma generalização para mais dois eventos.

De volta ao fio da meada, suponha que nós temos uma coleção $x_1,\ldots,x_n$ de variáveis subgaussianas, todas com parâmetro $\sigma$. Usando o meu argumento:

$$P\left(\max_{j=1,\ldots,n} |X_j| > t\right) = P\left(\bigcup_{j=1}^n |X_j| > t\right) \leq \sum_{j=1}^n P(|X_j| > t)$$

Agora, use a cota para uma variável subgaussiana:

$$P\left(\max_{j=1,\ldots,n} |X_j| > t\right) = P\left(\bigcup_{j=1}^n |X_j| > t\right) \leq \sum_{j=1}^n P(|X_j| > t) \leq \sum_{j=1}^ne^{-\frac{t^2}{2\sigma^2}} = ne^{-\frac{t^2}{2\sigma^2}}$$

Vamos deixar isso mais bonitinho: Faça $t = \sigma(\sqrt{2\log(n)} + \delta)$. Então:

$$t^2 = \sigma^2(\sqrt{2\log(n)} + \delta)^2$$

Se $a,b > 0$, então $(a+b)^2 \geq a^2 + b^2$. Considere os termos de t: $\sqrt{2\log(n)}$ é positivo e $\delta$ é sempre positivo, então:

$$t^2 = \sigma^2(\sqrt{2\log(n)} + \delta)^2 \geq \sigma^2(2\log(n) + \delta^2)$$

Multiplicando por $-1$ a gente inverte a desigualdade, logo:

$$P \left(\max_{j=1,\ldots,n} |X_j| > \sigma(\sqrt{2\log(n)} + \delta) \right) \leq n\exp \left(-\frac{\delta^2}{2} - \frac{2\log(n)}{2}\right) = e^{-\frac{\delta^2}{2}}$$

Na última igualdade, eu usei que $e^{-\log(n)} = \frac{1}{n}$

O que essas contas todas dizem? Primeiro, mesmo se todas as variáveis tem média zero, o máximo delas não vai estar centrado em zero: a gente ganhou um termo $\sigma\sqrt{2\log(n)}$. Esse termo é extremamente benevolente: ele cresce a raiz quadrada do log de n. Isso é bastante lento, como a figura abaixo mostra:

library(ggplot2)
library(latex2exp)
library(tidyr)

n <- 1:50
y <- sqrt(log(n))

df <- data.frame(n = n,y = y, id = n)
df <- pivot_longer(df,cols = c(y,id))

ggplot(df,aes(n,value,color = name)) + geom_abline() + geom_line()  + theme_light() + labs(x = "n", y = "", color = "") + scale_color_discrete(labels = c(id = expression(f(x)==x),y = expression(sqrt(log(n))))) 

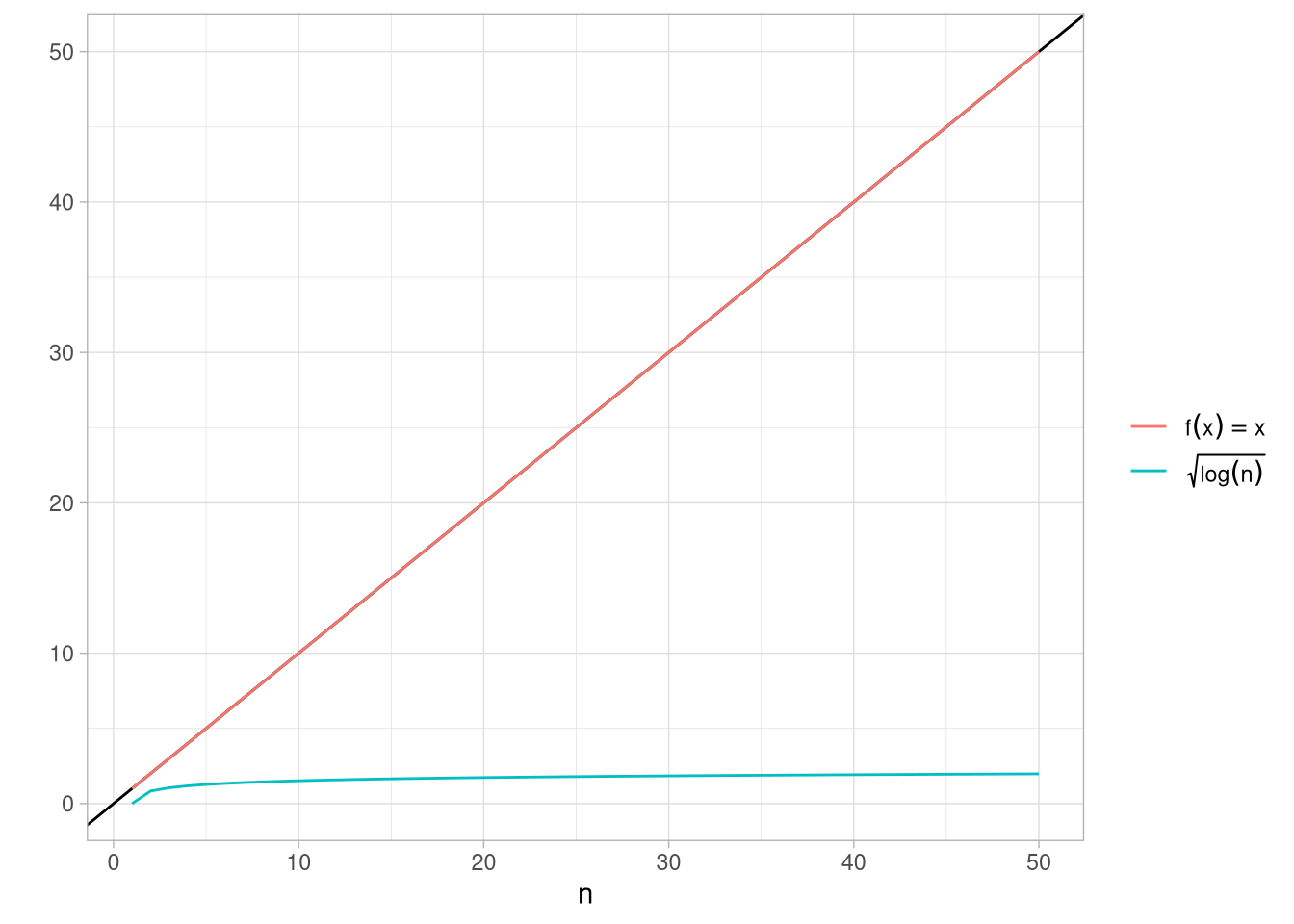
A segunda observação é que as chances do valor do máximo ser muito maior que $\sigma\sqrt{2\log(n)}$ é muito baixo: a cauda cai com a exponencial do quadrado, ou seja, a mesma velocidade da gaussiana.

Este post é estupidamente abstrato, mas ele vai ser necessário para um post no futuro que é um pouco menos abstrato.