Viés de variáveis instrumentais

Como prometido no post anterior, vamos usar simulação para testar algumas coisas. A primeira delas é um problema curioso e (relativamente) pouco explorado: o viés ao usarmos muitos instrumentos em variáveis instrumentais. O excelente Mostly Harmless Econometrics, de Angrist e Pischke, conta com uma discussão sobre o tema na seção 4.6.4 - não surpreendentemente chamada de Bias of 2SLS.

Antes, uma recapitulação sobre variáveis instrumentais (se você não aprendeu sobre variáveis instrumentais, qualquer livro básico de econometria vai falar sobre o tópico): suponha que você tem o modelo \(y =x\beta+e\) e você sabe que \(E(ex) \neq 0\) - ou seja, temos um problema de endogenidade. Suponha ainda que temos uma variável, \(z\), que é tal que \(E(xz) \neq 0\) e \(E(ez) = 0\) - a variável é dita relevante e exógena, respectivamente. Então, podemos usar Mínimos Quadrados em 2 Estágios (MQ2E) para obter uma estimativa do efeito de x sobre y.

Podemos ter mais instrumentos do que variáveis endógenas - um problema sobreidentificado - e parece razoável que queiramos usar todos os instrumentos para estimar o efeito de x sobre y. Afinal, estaríamos jogando fora informação se não usassemos todos os instrumentos, e definitivamente não queremos isso. O mínimos Quadrados em Dois Estágios permite isso.

Entretanto, variáveis instrumentais sofrem de um sério problema de viés quando se tem muitos instrumentos. Vamos ilustrar isso no caso que temos uma única variável endógena e ela é a única variável do problema. Nosso modelo vai ter duas equações:

\[y = u+\beta{}x+e \quad \quad (i)\] \[x = u + Z\Pi + v\]

Onde \(e\) e \(v\) são erros saídos de uma normal; \(u\) também é uma variável aleatória normal e que vai ser uma variável omitida correlacionada com o \(x\), por construção. No fim das contas, o erro da equação estrutural é \(u + e\), e como u também está na equação de do \(x\), a condição padrão de validade da estimativa de MQO é violada. Nosso interesse é no parâmetro \(\beta\).

Para fazer a simulação, iremos usar o comando ivreg do pacote AER (que eu carreguei silenciosamente no começo deste post). Ele recebe uma fórmula em duas partes: y ~ x, a fórmula estrutural \((i)\) e |z, os instrumentos. Vamos colocar todos os instrumentos com o mesmo coeficiente 1, ou seja \(\Pi\) vai ser uma coluna de 1. Vamos testar estimar o modelo com diferentes quantidades de instrumentos. Veja que, quando eu criar o modelo, todos os instrumentos vão ser relevantes, então o problema não é selecionar os instrumentos certos. Se fossemos fazer a coisa certa, teríamos que usar todos os instrumentos. Mas o MQ2E vai gerar estimativas viesadas quando colocarmos todos os instrumentos.

Uma iteração da nossa simulação é da seguinte forma:

set.seed(1653)

cf <- rep(0,20) #os coeficientes vão entrar aqui
n <- 100#tamanho da amostra

u <- rnorm(n)
z <- matrix(rnorm(n*20),ncol = 20) #teremos 20 instrumento

x <- u + z%*%rep(1,ncol(z)) + rnorm(n)
y <- u + x + rnorm(100)

for(j in 1:ncol(z)){
  cf[j] <- coef(ivreg(y ~ x|z[,1:j]))[2]
}

Vamos analisar isso: pontos são a estimativa usando uma certa quantidade de instrumentos (o eixo x vai mostrar quantos instrumentos temos). A linha vermelha mostra o valor do coeficiente estimado por MQO - que sabemos que será viesado - e a linha verde o valor verdadeiro do coeficiente

mqo <- coef(lm(y ~ x))[2]

lb <- min(min(cf),mqo,1)
up <- max(max(cf),mqo,1)

plot(1:ncol(z),cf, ylim = c(lb,up))
lines(1:length(cf),rep(mqo,length(cf)),col = 2)
lines(1:length(cf),rep(1,length(cf)),col = 3)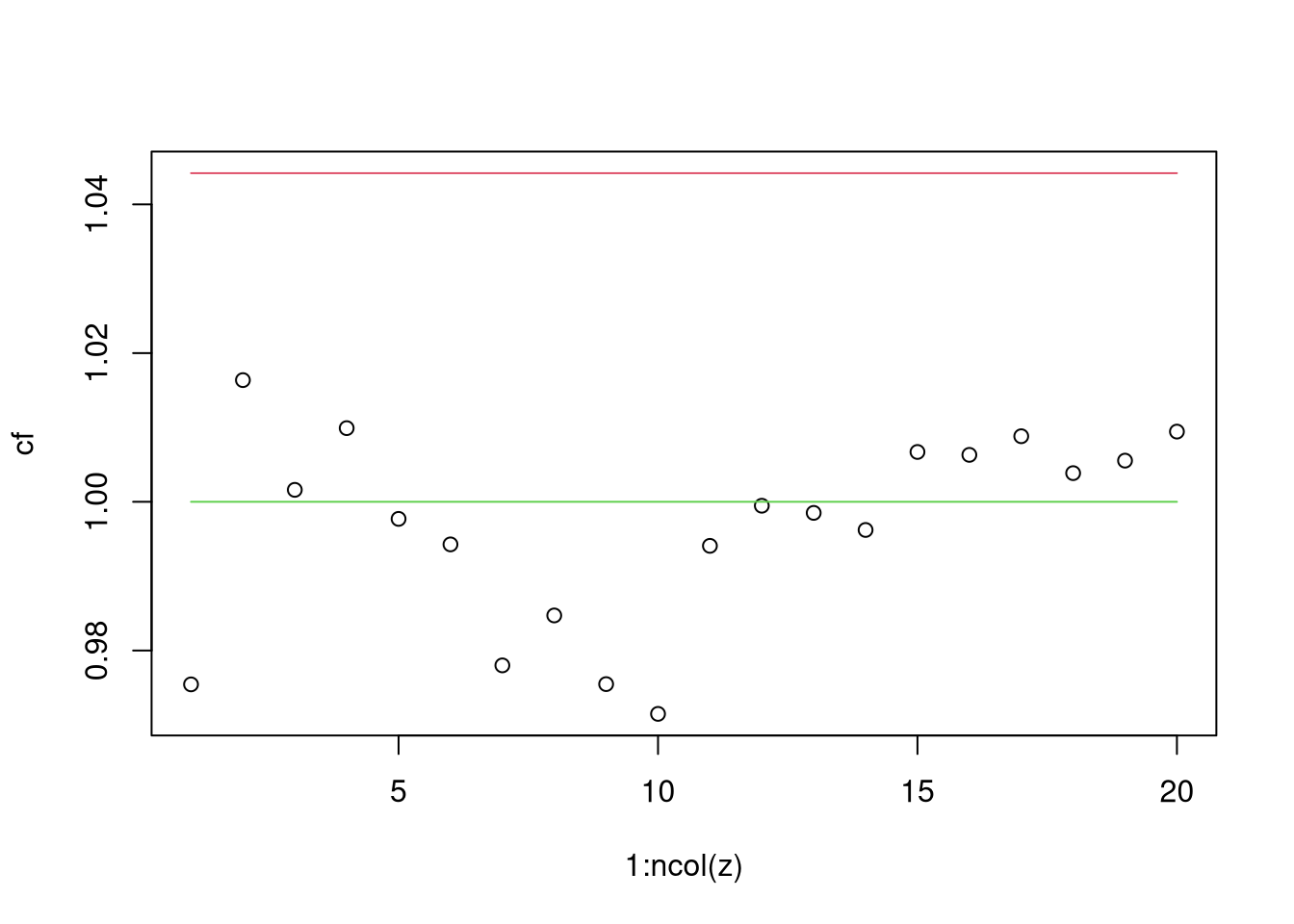

Veja que o lb e up só acertam o tamanho do plot para a linha vermelha aparecer: o viés de MQO é o pior, como fica bem claro.

Obviamente, com só uma simulação é muito difícil afirmar qualquer coisa - é literalmente fazer inferência com uma observação. O código abaixo cria uma função que repete a simulação acima mil vezes. Como se pode imaginar, essa simulação é lenta, então eu deixo o código paralelizado na hora de estimar o \(\beta\) com diferentes quantidades de instrumento. Isso exige que você registre um cluster no R e use o pacote foreach.

vies <- function(n,k,peso=1){
  
  cf <- matrix(0,ncol = k, nrow = 1000)
  mqo <- rep(0,1000)
  
  for(i in 1:1000){
    z <- matrix(rnorm(n*k),ncol = k)
    u <- rnorm(n)
    
    x <- peso*u + z%*%rep(1,k) + rnorm(n) #esse peso vai ficar claro mais embaixo
    
    y <- u + x + rnorm(n)
    
    mqo[i] <- coef(lm(y ~ x))[2]
    
    aux <- foreach(j = 1:ncol(z), .packages = "AER", .combine = c) %dopar% {
      mod <- ivreg(y ~ x|z[,1:j])
      coef(mod)[2]
    }
    cf[i,] <- aux
    print(i)
  }
  resposta <- list("mqo" = mqo,"iv" = cf)
    return(resposta)
}

O foreach funciona como o for, mas cria um objeto com o resultado do loop, o que pode dificultar as coisas em alguns casos, como o nosso, que queremos obter o coeficiente de cada caso da variável instrumental e de MQO. Podemos usar o ˜foreach˜ Vamos começar testando com 100 observações e no máximo 50 instrumentos. Obteremos o seguinte plot quando tirarmos a média:

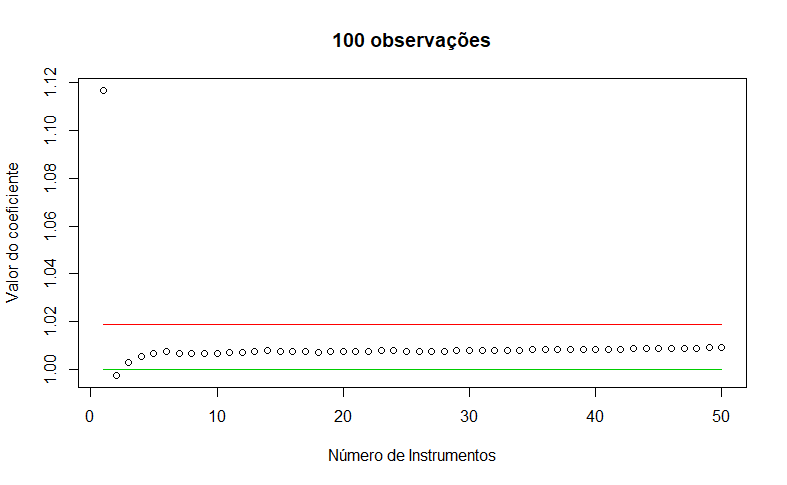
Veja que o caso com um único instrumento gera um valor do coeficiente tão grande - muito maior que o viés do estimador de MQO - que o gráfico basicamente “esconde” o que acontece depois. Vamos tirar o primeiro ponto e ver o que acontece:

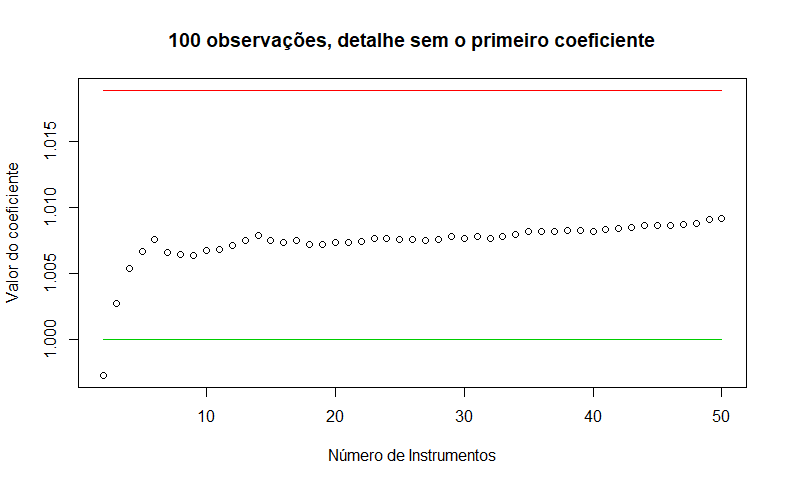
Lembre que o modelo verdadeiro tem 50 variáveis que podem ser usadas como instrumentos, mas usar qualquer coisa acima de 10 já gera um viés brutal. Por incrível que pareça, 2 ou 3 variáveis instrumentais minimizam o viés da estimação.

Antes de continuar, é necessário chamar atenção para alguns pontos:

1. O caso de um instrumento é um desastre porque temos 50 instrumentos possíveis. Se repetissimos a simulação com o caso do modelo verdadeiro ter 1 ou dois instrumentos, usar variável instrumental seria muito melhor do que usar MQO

2. Veja que o viés de MQO não é tão grande assim: é maior que o viés de IV, mas não é tão grande assim. Dado a dificuldade de se encontrar um bom instrumento, por que então não viver com o viés? Veja que isso é uma característica de como o problema foi escrito: o fator que gera viés tem peso 1, enquanto os instrumentos tem um peso muito maior - afinal, temos cinquenta instrumentos. Peco pelo excesso, mas um exemplo pode ajudar: é a mesma coisa que tentar ouvir alguém falando em uma sala com barulho. Se o barulho é de um restaurante mais ou menos vazio, é relativamente fácil. Em uma boate, a conversa é indecifrável. Ter 50 instrumentos contra só uma variável que gera a correlação entre \(x\) e \(e\), que tem coeficiente 1, gera um viés pequeno. Por isso que existe a variável peso na função: se aumentarmos o peso de \(u\), a estimativa de MQO vai ficar bem pior. O exemplo abaixo ilustra isso: colocamos peso 10 e apenas 100 observações.

Mais um caso, em que colocamos peso 50(!) e temos 5000 observações, ilustrando que o problema ocorre mesmo com amostras relativamente grandes:

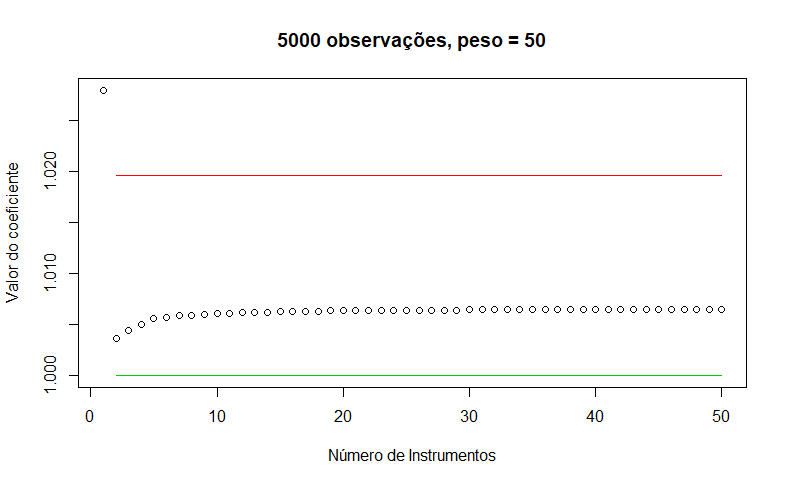
As simulações acima chamam atenção para o fato de que muitos instrumentos geram viés na estimação por MQ2E, apesar das muitas vantagens de usar muitos instrumentos (testes de sobreidentificação, por exemplo). Idealmente, dois instrumentos aproximam a estimação do valor verdadeiro. Mas é um estudo por simulação: não sabemos o quão geral são essas regras e quais características que colocamos na simulação podem ser relaxadas para gerar um resultado semelhante.