August 12, 2019

1701 palavras 8 mins

A Abordagem de Ponto Fixo para o Teorema de Perron-Frobenius Parte II: Demonstração e Verificação Computacional

@PedrooCava

Um Pequeno Aviso

Este post é - como o nome indica - uma continuação de outro. Sua leitura solitária pode fazer pouco ou nenhum sentido se o leitor não está familiarizado com os conceitos introduzidos na primeira parte.

Plano de Voo

Na primeira parte fomos apresentados a muita coisa então vale a pena refresca-las um pouco antes de entender para onde vamos. Primeiro conhecemos o conceito de ponto fixo. Depois de verificar que é relativamente simples encontrar pontos fixos em funções afins, percebemos que a tarefa fica bem complexa em pouco tempo e que por isso é interessante usar Teoremas de Ponto Fixo para garantir a existência destes objetos para certas funções que atendem a determinados critérios. Nos focamos no Teorema do Ponto Fixo de Brouwer, que garante que toda funções contínua com domínio fechado, limitado e convexo e imagem neste mesmo conjunto admite pelo menos um ponto fixo.

Provamos esse resultado em três casos particulares, cada um se beneficiando de estratégias de provas bem diferentes. Primeiro vimos que com ferramentas simples do Cálculo conseguíamos demonstrar a existência de ponto fixo em funções que mapeiam o fechado $[0,1]$ nele próprio - bem como a interpretação geométrica associada. Depois usamos o Lema da Não-Retração para mostrar que não é tão difícil provar a validade do teorema em duas dimensões. Pelo contrário, era uma decorrência bem intuitiva de compor retas entre pontos em um círculo. Por fim, depois de apresentados o conceito de Simplex e de Colorações de Sperner, usamos um argumento de Combinatória para mostrar que até em dimensões arbitrariamente grandes o resultado valia.

E por que eu dediquei algumas páginas de texto e semanas da minha vida escrevendo a primeira parte? Bem, porque eu acho que demonstra-lo é (i) interessante em si e deixa tudo menos “caído dos céus” e (ii) porque no meio do caminho ganhei motivos para introduzir suave e contextualizadamente vários conceitos que usaremos na demonstração do Teorema de Perron-Frobenius.

Depois da longa parte I, precisamos agora conhecer apenas mais um conceito e estamos prontos para chegar no Teorema de Perron-Frobenius.

Irredutibilidade

Definição: Dizemos que uma matriz $A_{n \times n} = [a_{ij}]$ é redutível se seus índices $1,2,...n$ podem ser divididos em dois conjuntos não-vazios e disjuntos $i_1, i_2,..., i_p$ e $j_1,j_2,...,j_q$ (respeitando a limitação de que $p+q =n$, não podendo “criar dimensões”) de forma que qualquer elemento $a_{ij}$ da matriz que tenha índices nesses conjuntos seja igual a $0$.

Essa definição seca pode parecer estranha, mas tem uma interpretação mais visual muito intituiva. Uma matriz é redutível se podemos rearranjar suas linhas e colunas de forma que ela tenha um “bloco” de zeros.

Imagine que temos uma matriz $2$ por $2$ em que cada entrada é uma matriz quadrada $n$ por $n$. $A$, $B$ e $C$ são matrizes com elementos quaisquer e $\mathbf{0}$ é uma matriz preenchida de zeros. Se uma matriz $D$ é redutível, então admite uma representação assim:

\[D = \begin{pmatrix}A & C \\ \mathbf{0} & B\\ \end{pmatrix}\]

Em mais detalhes:

\[D = \begin{pmatrix}\begin{bmatrix} a_{11} &a_{12} &\ldots & a_{1n} \\ a_{21} &a_{22} &\ldots & a_{2n} \\ \vdots & \ddots & \ddots &\vdots \\ a_{11} &a_{12} &\dots & a_{nn} \\ \end{bmatrix} & \begin{bmatrix} c_{11} &c_{12} &\ldots & c_{1n} \\ c_{21} &c_{22} &\ldots & a_{2n} \\ \vdots & \ddots & \ddots &\vdots \\ c_{n1} &c_{n2} &\dots & c_{nn} \\ \end{bmatrix} \\ \\ \begin{bmatrix} 0 &0 &\ldots & 0 \\ 0 &0 &\ldots & 0 \\ \vdots & \ddots & \ddots &\vdots \\ 0 &0 &\dots & 0 \\ \end{bmatrix}& \begin{bmatrix} b_{11} &b_{12} &\ldots & b_{1n} \\ b_{21} &b_{22} &\ldots & b_{2n} \\ \vdots & \ddots & \ddots &\vdots \\ b_{n1} &b_{n2} &\dots & b_{nn} \\ \end{bmatrix}\\ \end{pmatrix}\]

Embora a matriz de zeros esteja na entrada esquerda inferior neste exemplo, $D$ seria redutível se conseguíssemos rearranjar seus vetores de forma que a matriz de zeros fosse formada em qualquer canto.

O Resultado Principal

O enunciado do Teorema de Perron-Frobenius pode ser posto de várias maneiras, existem várias maneiras equivalentes de frasea-lo. Vou optar por duas:

Teorema (Perron-Frobenius, formulação de Kohlberg and Pratt (1982)): Se $A$ é um operador linear positivo, então existe algum $l \in \mathbb{R}^m$ tal que: \[\frac{A^n x}{||A^nx||} \to \frac{l}{||l||}\]
Teorema (Perron-Frobenius, formulação adaptada de Meyer (2000)): Seja $A$ uma matriz positiva e irrudutível $m \times m$. Então vale que existe um único autovetor positivo de $A$ (que chamaremos de autovetor de Perron-Frobenius) cujo autovalor associado é maior do que o de qualquer outro autovetor de $A$. Mais ainda, se notarmos este autovalor como $\lambda$, então vale que $\text{min} \sum_j A_{ij} \leq \lambda \leq \text{max} \sum_j A_{ij}$.

Primeiro vamos usar o Teorema do Ponto Fixo de Brouwer para mostrar que necessariamente existe algum autovetor de Perron-Frobenius.

Proposição (Existência do Autovetor de Perron-Frobenius): Seja $A$ uma matriz irredutível e positiva. $A$ tem pelo menos um autovetor positivo cujo autovalor também é positivo.
Prova: Tome $v \in \Delta_n$. Como $A$ é irredutível, $Av$ não pode ser o vetor nulo. Defina $f:\Delta_n \to \Delta_n$ como $f(v) = (Av)(||Av||_{1})^{-1}$. Pelo Teorema do Ponto Fixo de Brouwer necessariamente existe pelo menos um vetor $v'$ que é ponto fixo de $f$. Note que por $v' \in \Delta_n$, é positivo. Então temos $v'(||Av'||_{1}) = Av'$. $v'$ é autovetor de $A$ com autovalor dado pela norma $1$ de $A$ aplicada em $v'$. Como $A$ é positiva, a norma $1$ de sua aplicação em um vetor positivo necessariamente também é positiva e assim acabou a prova.

Acabamos de provar existência de um autovetor positivo usando o Ponto Fixo de Brouwer para isso, mas observe que isso não implica unicidade. Afinal, o argumento se apoia no fato de que $f:\Delta_n \to \Delta_n$ admite pelo menos um ponto fixo, mas isso não nos garante que teremos somente um ponto fixo. $A$ terá exatamente $\# \mathbb{F}(f)$ autovetores positivos. Como podemos mostrar que teremos apenas um? Com o nosso amigo o Teorema do Ponto Fixo de Banach.

Proposição (Unicidade do Autovetor de Perron-Frobenius): $v'$ é o único autovetor positivo de $A$.
Prova: Defina $P$ como conjunto de vetores com todas as entradas não-negativas no $\mathbb{R}^n$. Defina a transformação $T$ como sendo $Av/||Av||$. Aplincando $T$ em $P$ teremos um subconjunto próprio de $P$, então $T$ é uma contração que necessariamente tem um e somente um ponto fixo $v'$, então temos: $T(v') = v'$, o que implica $Av'/||Av'|| = v'$ que por sua vez implica $Av' = ||Av'||v'$. Então $v'$ é o único autovetor positivo de $A$.

Note que encontramos o autovalor do nosso autovetor positivo, chamaremos esse autovalor de $\lambda = ||Av'||$. Temos outra proposição, agora uma que relaciona $\lambda$ aos outros autovalores de $A$.

Proposição (Dominância do Autovalor de Perron): Qualquer outro autovalor $\mu$ de $A$ é menor em módulo do que $\lambda$.

A prova é um brain-teaser interessante, apesar de simples, então vou deixar apenas um esboço parcial aqui e deixo o resto como exercício¹.

Esboço: Escolha um autovetor $w$ de $A$ com autovalor $\lambda'$. Como mostramos, $w$ tem pelo menos alguma entrada negativa. Vamos nos referir ao vetor $|w|$ definido como $|w|_i = |w_i|$ de forma que $|w|$ sempre seja positivo. Temos $\mu w_i = \sum_j A_{ij}w_j$. Para o leitor que quiser terminar: explore o fato de que $A_{ij}$ é sempre um número positivo e de que pelo menos uma entrada de $w$ é negativa. Use nosso velho amigo módulo.

Verificando esse resultado computacionalmente

A função eigen() faz a decomposição espectral de matrizes com métodos numéricos então a usaremos para aproximar os autovalores e vetores de várias matrizes simuladas e além disso traz algumas comodidades. O vetor com os autovalores $values está na ordem de associação com os vetores colunas da matriz de autovetores $vectors.

set.seed(1234)
n = 1000
m = 4
t = 20


DF = tibble(autovalor = rep(NA, each = n),
            automin = rep(NA, each = n),
            automax = rep(NA, each = n),
            marcador = rep(NA, each = n))

for(i in 1:n) {

A = runif(n = m) %>% 
  round(digits = 2) %>%
  matrix(ncol = 2)  # uma matriz positiva

auto = eigen(A)
marcador = ifelse((auto$values[1] >= min(rowSums(A))) & (auto$values[1] <= max(rowSums(A))),
                  TRUE,
                  FALSE)

DF$autovalor[i] = auto$values[1]
DF$automin[i] = min(rowSums(A))
DF$automax[i] = max(rowSums(A))
DF$marcador[i] = marcador

}

Será que de fato $\text{min} \sum_j A_{ij} \leq \lambda \leq \text{max} \sum_j A_{ij}$?

table(DF$marcador) %>% knitr::kable()

Var1	Freq
FALSE	1
TRUE	999

Como por questões de aproximação o R pode marcar falso para alguns vetores, vamos inspeciona-los:

DF %>% filter(marcador == FALSE) # seleciona apenas os vetores que retornaram falso

## # A tibble: 1 x 4
##   autovalor automin automax marcador
##       <dbl>   <dbl>   <dbl> <lgl>   
## 1      1.49    1.49    1.49 FALSE

Como diria um professor de física que tive no ensino médio, a matemática é soberana. De fato, o autovalor de Peron-Frobenius é limitado, superior e inferiormente, pelas somas em linhas da matriz $A$.

E podemos também ver a formualação de Kohlberg-Pratt funcionando. Afinal, o Teorema de Perron-Frobenius é sim uma espécie de teorema de ponto fixo. Como na parte anterior em que animamos o Ponto Fixo de Banach ocorrendo, veremos algo muito similar.

matriz = runif(n = m) %>% 
  round(digits = 2) %>% 
  matrix(ncol = 2)

matriz = matriz/base::norm(matriz)


### dividir pela norma
 DF = tibble(R1 = rep(NA, times = (n*t)),
              R2 = rep(NA, times = (n*t)),
              t = rep(NA, times = (n*t)))
  

for(j in 1:n) {

  vetor = c(rnorm(n = sqrt(m), sd = m*2) %>% round(digits = 2)) # inicializamos um vetor

 
  for(i in 1:t) {
  
  indice =  if(j > 1) {ifelse(((j*t) + i) > (t*n), 
                              (t*n), 
                              ifelse(j > 1, (j*t) + i, i))} 
              else { indice = i}   # trambicagem para o índice correr corretamente

  vlinha = (matriz^i) %*% vetor  # aplicamos a matriz

  
  DF$R1[indice] =  vlinha[1] 
  DF$R2[indice] =  vlinha[2]
  DF$t[indice] = i
  
  }
  
  rm(vetor)

}
 
DF = tidyr::drop_na(DF)


g = DF %>% ggplot(aes(x = R1, y = R2, colour = t)) + 
  theme(legend.title = element_blank(),
        legend.position = "none") +
  geom_point() + 
  geom_density_2d() +
  transition_time(t) +   
  ease_aes('linear') +
  labs(x = "",
       y = "") 

animate(g, fps = 30)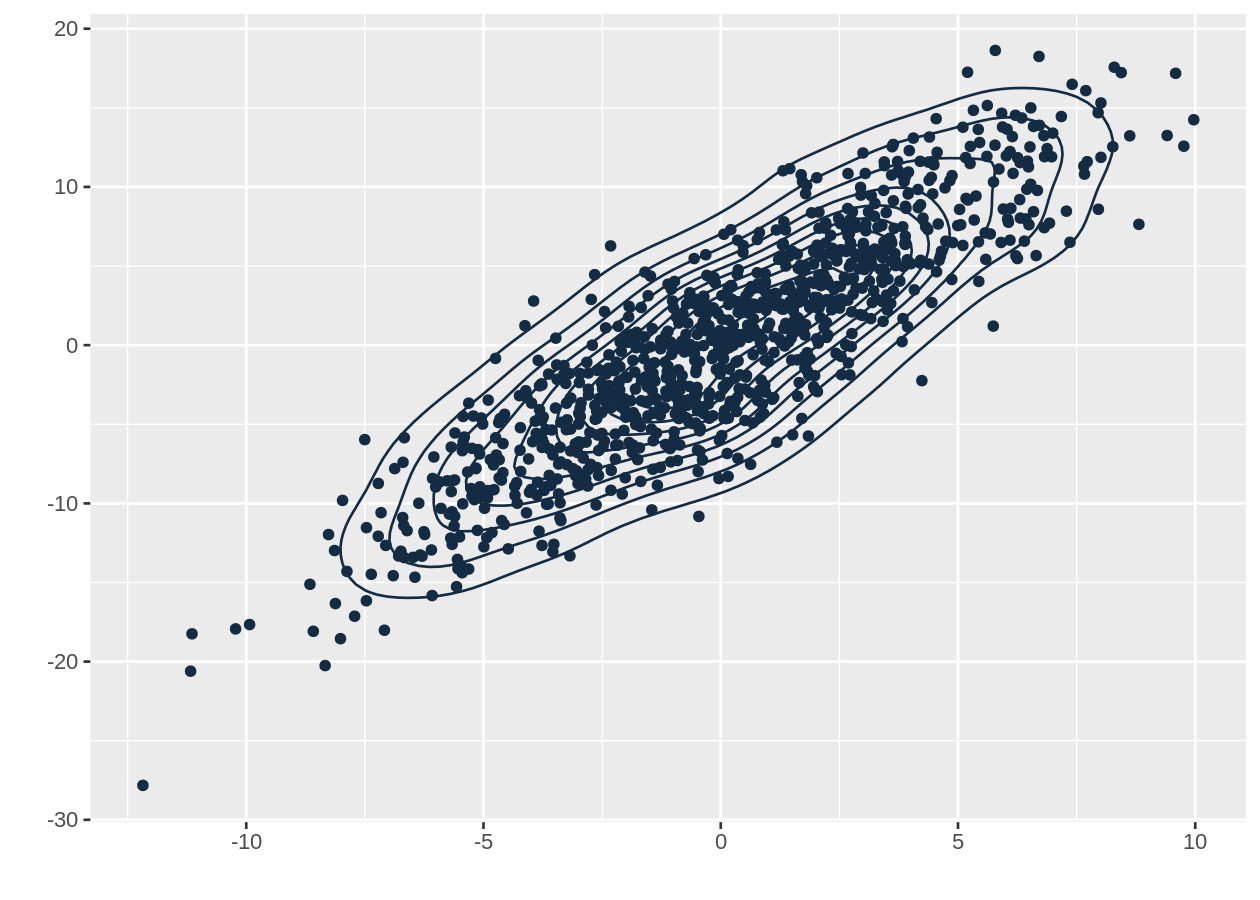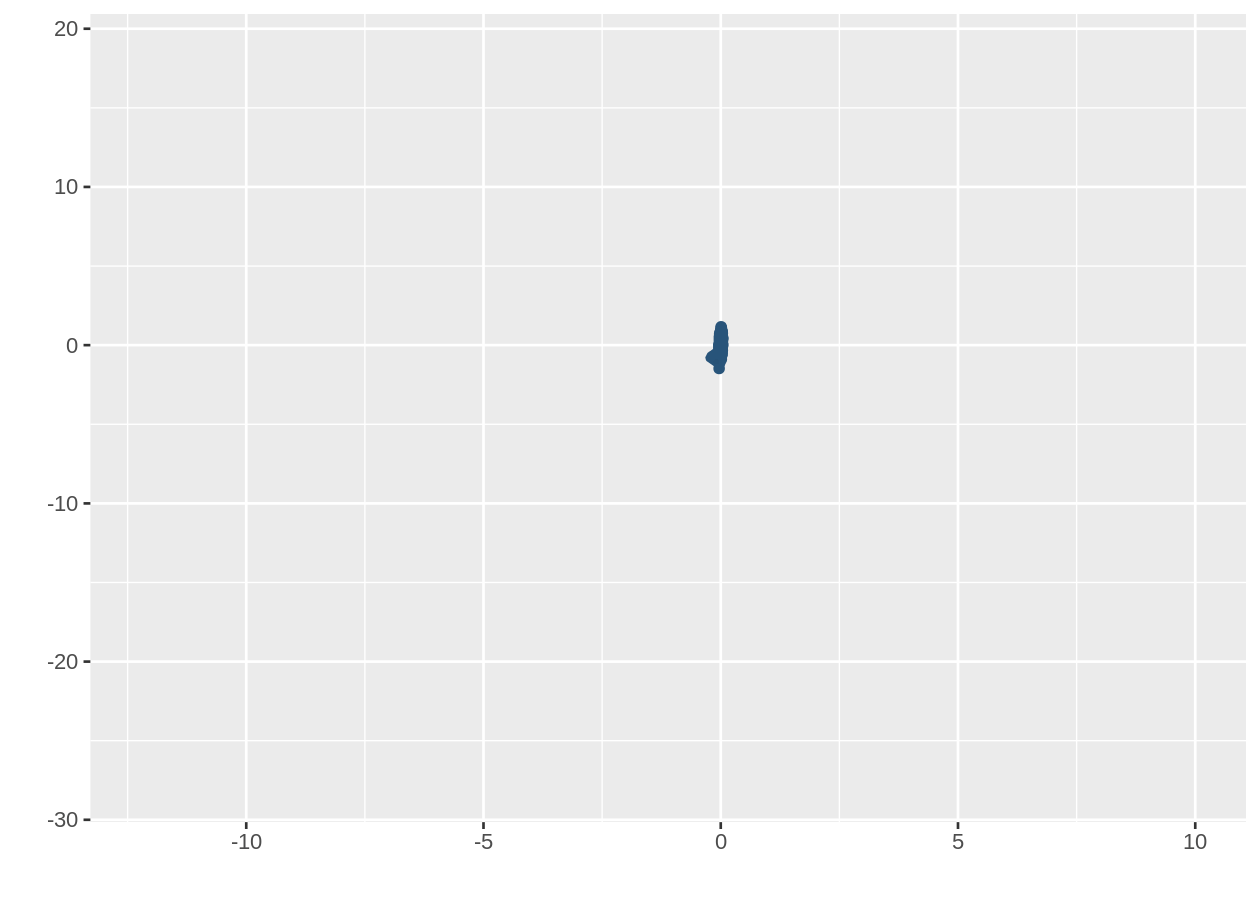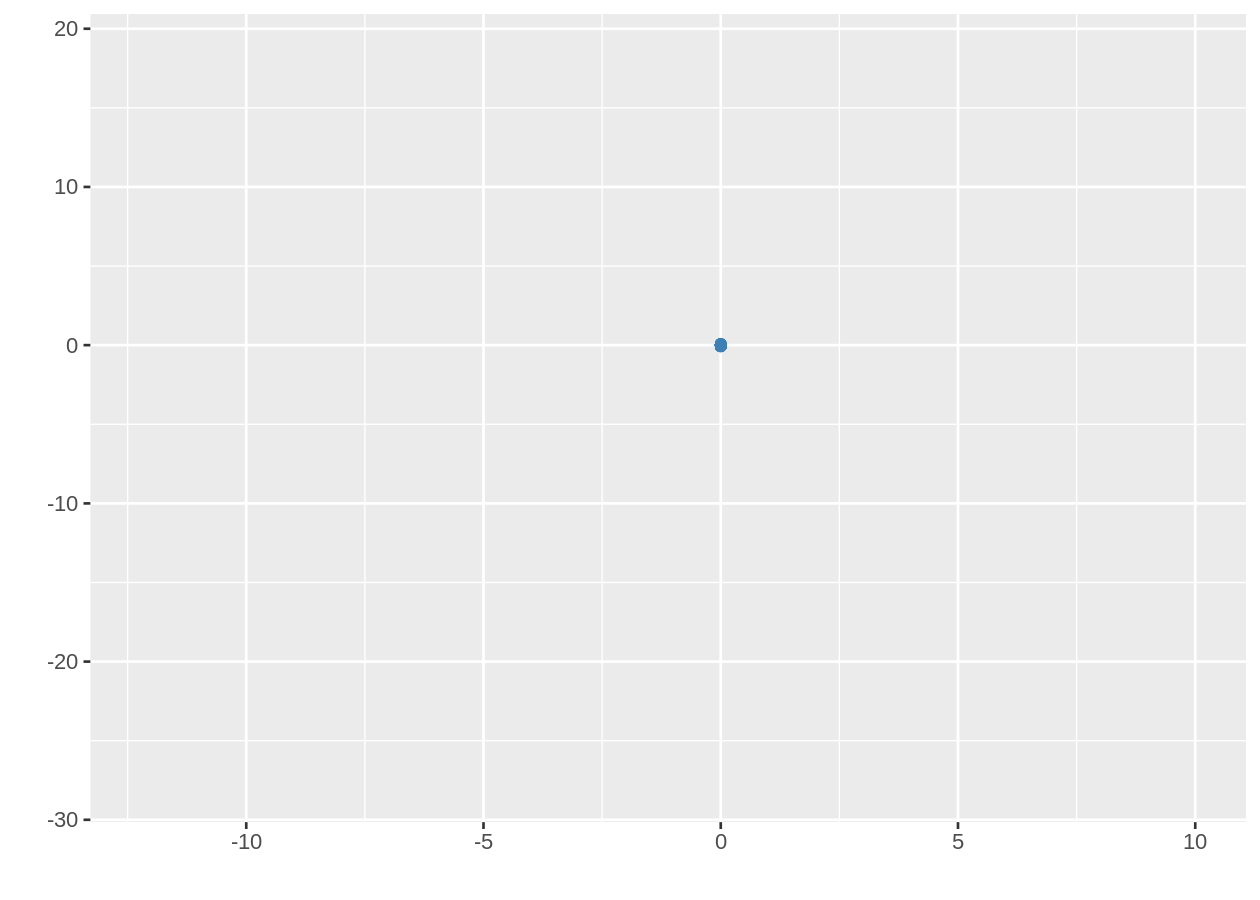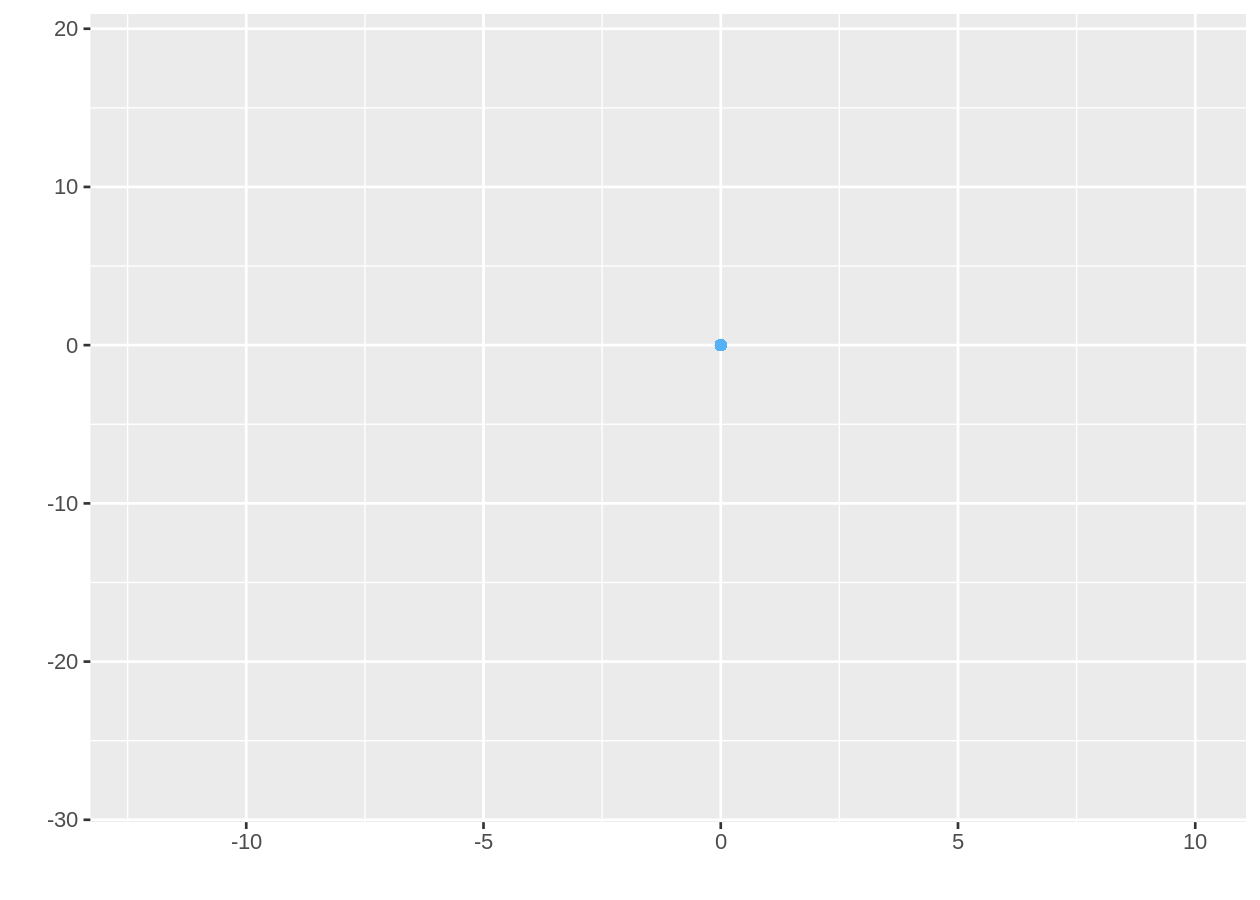

Referências

Kohlberg, Elon, and John W Pratt. 1982. “The Contraction Mapping Approach to the Perron-Frobenius Theory: Why Hilbert’s Metric?” Mathematics of Operations Research 7 (2). INFORMS: 198–210.

Meyer, Carl D. 2000. Matrix Analysis and Applied Linear Algebra. Vol. 71. Siam.

Eu sempre quis fazer isso↩