Classificando distribuições a partir dos momentos

Pedro Cavalcante
@PedrooCava

Surgiu uma curiosidade legítima na minha cabeça ontem e eu queria saber se consigo, a partir dos momentos amostrais, treinar um classificador razoável para a família do processo gerador. Responder isso vai ser divertido porque é um bom playgrond para ferramentas do tidyverse e deixa de exemplo um fluxo mínimo de modelagem com tidymodels.

A primeira coisa a fazer é uma função que recebe um nome de função que possa gerar dados aleatórios seguindo algum processo conhecido - o parâmetro dgp vem de data generating process. Vou parametrizar ela menos do que é possível porque, putz moh trabalho.

process_factory <- function(dgp, n = 100) {
  
  if(dgp == "rnorm") {
    
    to_be_called <- call("rnorm", 
                         n = n, 
                         sd = runif(1, 0, 3), 
                         mean = runif(1, -3, 3))
  
  } else if(dgp == "rt") {
    
    to_be_called <- call("rt", 
                         n = n, 
                         df = sample(1:30, 1), 
                         ncp = runif(1, 0, 10))
    
  } else if(dgp == "runif") {
    
    to_be_called <- call("runif",
                         n = n,
                         min = runif(1, -3, 0),
                         max = runif(1, 0, 3))
    
    } else if(dgp == "rexp") {
   
   to_be_called <- call("rexp", 
                        n = n, 
                        rate = runif(1, 0, 3))
  
    } else if(dgp == "rgamma") {

    to_be_called <- call("rgamma", 
                         n = n, 
                         shape = runif(1, 0, 3),
                         scale = (1/runif(1, 0, 3)) + rnorm(1, sd = .2))
      
    }
  
  eval(to_be_called)
      
}

Agora uma função que recebe um vetor com dados simulados com algum processo gerador dado e retorna os primeiros \(k\) momentos amostrais.

first_kmoments <- function(process, .min_k = 1, .k = 20, .center = TRUE) {
  
  tibble(process = list(process)) %>%
    list() %>%
    rep(times = .k) %>%
    reduce(bind_rows) %>%
    mutate(K = .min_k:.k,
           moment = map2_dbl(
             .x = process, 
             .y = K,
             ~ moment(x = .x, order = .y, center = .center))) %>%
    pivot_wider(values_from = moment, 
                names_from = K, 
                names_prefix = "moment_") %>%
    select(-process)
  
}

(Tem um bug bem fácil de consertar e de reproduzir na função acima, fica como exercício)

Beleza agora podemos de fato simular alguns dados e pedir os momentos das distribuições simuladas.

library(tidyverse)
library(e1071)
library(magrittr)

(tibble(
  dgp = # variável com o nome dos processos, o Y do nosso modelo
   sample(c("rnorm", "runif", "rexp", "rgamma", "rt"), # amostre um de 4 nomes 
          size = 10000, # 100000 vezes
          replace = TRUE), # com substituição
   moments = # variável momentos que irá conter uma lista de dataframes
       map(dgp, # itere sobre o vetor com nomes de dgps
           ~ first_kmoments(process_factory(.x)))) %>% 
  unnest(moments) %>% # desaninha a lista de dataframes
  na.omit() ->
  data)

## # A tibble: 9,981 x 21
##    dgp    moment_1 moment_2 moment_3 moment_4 moment_5 moment_6  moment_7
##    <chr>     <dbl>    <dbl>    <dbl>    <dbl>    <dbl>    <dbl>     <dbl>
##  1 runif  2.22e-18   2.47   -8.95e-3  1.02e+1  3.48e-2 4.91e+ 1  1.49e+ 0
##  2 rt     3.20e-16  12.4     6.30e+1  9.49e+2  1.11e+4 1.57e+ 5  2.23e+ 6
##  3 runif -1.11e-17   0.528  -3.29e-2  5.86e-1 -1.25e-1 8.24e- 1 -3.28e- 1
##  4 rnorm  2.22e-16   0.970   2.19e-1  2.20e+0  1.14e+0 6.63e+ 0  5.35e+ 0
##  5 rt     5.86e-16   2.59    2.10e+0  2.10e+1  4.57e+1 2.86e+ 2  9.57e+ 2
##  6 rt     6.39e-16 826.      1.20e+5  2.07e+7  3.68e+9 6.62e+11  1.20e+14
##  7 runif -2.50e-18   0.0904  8.14e-4  1.45e-2 -8.97e-5 2.81e- 3 -1.03e- 4
##  8 runif  1.61e-17   0.457  -4.20e-2  3.73e-1 -7.06e-2 3.72e- 1 -1.04e- 1
##  9 runif  1.55e-17   0.831  -1.32e-1  1.23e+0 -4.43e-1 2.18e+ 0 -1.20e+ 0
## 10 rt    -2.13e-16   2.47    3.75e+0  2.51e+1  8.53e+1 4.46e+ 2  1.97e+ 3
## # … with 9,971 more rows, and 13 more variables: moment_8 <dbl>,
## #   moment_9 <dbl>, moment_10 <dbl>, moment_11 <dbl>, moment_12 <dbl>,
## #   moment_13 <dbl>, moment_14 <dbl>, moment_15 <dbl>, moment_16 <dbl>,
## #   moment_17 <dbl>, moment_18 <dbl>, moment_19 <dbl>, moment_20 <dbl>

Como são dados 100% simulados eu não vejo a virtude de explorar graficamente, vou pular então. Agora vamos treinar uma grade de modelos Random Forest.

library(tidymodels)

doParallel::registerDoParallel() # executar em paralelo

data_split <- initial_split(data, strata = dgp) # divisão dos dados
data_treino <- training(data_split) # treino
data_teste <- testing(data_split) # teste

data_rec <- recipe(dgp ~ ., data = data_treino) 
data_prep <- prep(data_rec) 

(modelo_tune <- rand_forest( # especificação da grade a ser avaliada
  mtry = tune(),
  trees = 1000,
  min_n = tune()) %>%
  set_mode("classification") %>%
  set_engine("randomForest"))

## Random Forest Model Specification (classification)
## 
## Main Arguments:
##   mtry = tune()
##   trees = 1000
##   min_n = tune()
## 
## Computational engine: randomForest

(modelo_workflow <- workflow() %>%
  add_recipe(data_rec) %>%
  add_model(modelo_tune))

## ══ Workflow ═══════════════════════════════════════════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: rand_forest()
## 
## ── Preprocessor ───────────────────────────────────────────────────────────────────────────────────────────
## 0 Recipe Steps
## 
## ── Model ──────────────────────────────────────────────────────────────────────────────────────────────────
## Random Forest Model Specification (classification)
## 
## Main Arguments:
##   mtry = tune()
##   trees = 1000
##   min_n = tune()
## 
## Computational engine: randomForest

(data_folds <- vfold_cv(data_treino, 5))

## #  5-fold cross-validation 
## # A tibble: 5 x 2
##   splits            id   
##   <list>            <chr>
## 1 <split [6K/1.5K]> Fold1
## 2 <split [6K/1.5K]> Fold2
## 3 <split [6K/1.5K]> Fold3
## 4 <split [6K/1.5K]> Fold4
## 5 <split [6K/1.5K]> Fold5

O passo final é “afinar” a grade e estimar todos os modelos seguindo o workflow.

(tune_results <- tune_grid(
  modelo_workflow,
  resamples = data_folds,
  grid = 20
))

Vamos avaliar brevemente a área abaixo da curva ROC dos vários modelos que treinamos.

tune_results %>%
  collect_metrics(summarize = FALSE) %>%
  filter(.metric == "roc_auc") %>%
  ggplot(aes(x = .estimate)) +
  geom_histogram(fill = "light green") +
  labs(title = "Distribuição das AUROC",
       x = "AUROC",
       y = "") +
  scale_x_continuous(labels = scales::percent) +
  theme_minimal()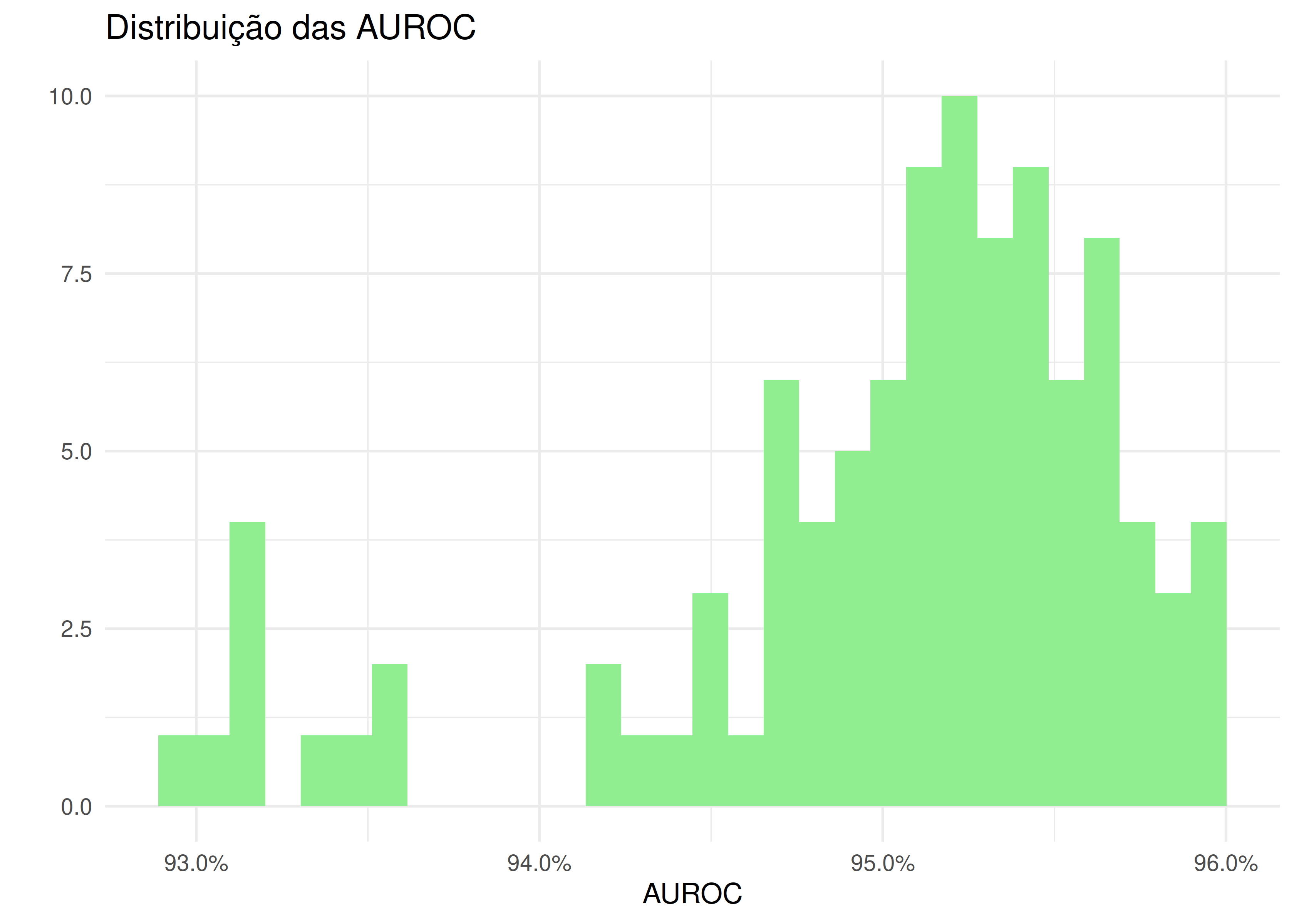

A primeira vez que rodei tudo me deu AUROCs beeem altas, além dos 95%. Em classificação binária, na maioria dos domínios de aplicação, isso é alto demais para ser verdade, mas problemas multiclasse normalmente vêm com AUROCs altas. Vamos olhar com mais cuidado para o melhor modelo - ainda dentro da amostra de treino.

library(vip)

(melhor_auc <- select_best(tune_results, "roc_auc"))

## # A tibble: 1 x 3
##    mtry min_n .config
##   <int> <int> <chr>  
## 1    14     9 Model01

(modelo_final <- finalize_model(modelo_tune, melhor_auc))

## Random Forest Model Specification (classification)
## 
## Main Arguments:
##   mtry = 14
##   trees = 1000
##   min_n = 9
## 
## Computational engine: randomForest

(avaliacao <- modelo_final %>%
  set_engine("randomForest") %>%
  fit(dgp ~ ., data = juice(data_prep)))

## parsnip model object
## 
## Fit time:  16.4s 
## 
## Call:
##  randomForest(x = as.data.frame(x), y = y, ntree = ~1000, mtry = ~14L,      nodesize = ~9L) 
##                Type of random forest: classification
##                      Number of trees: 1000
## No. of variables tried at each split: 14
## 
##         OOB estimate of  error rate: 21.09%
## Confusion matrix:
##        rexp rgamma rnorm   rt runif class.error
## rexp   1024    387     0   48     0  0.29814942
## rgamma  514    768     8  140     1  0.46331237
## rnorm     0     12  1309  160    37  0.13768116
## rt       40     93   110 1320     6  0.15869981
## runif     0      6    16    1  1488  0.01522171

Interessante que algumas distribuições são particularmente difíceis de acertar, como a gama. A uniforme e a normal, por exemplo, são beeem mais fáceis de acertar.

vip(avaliacao, geom = "col", fill = "light green") +
  labs(title = "Importância de variáveis para o classificador") +
  theme_minimal()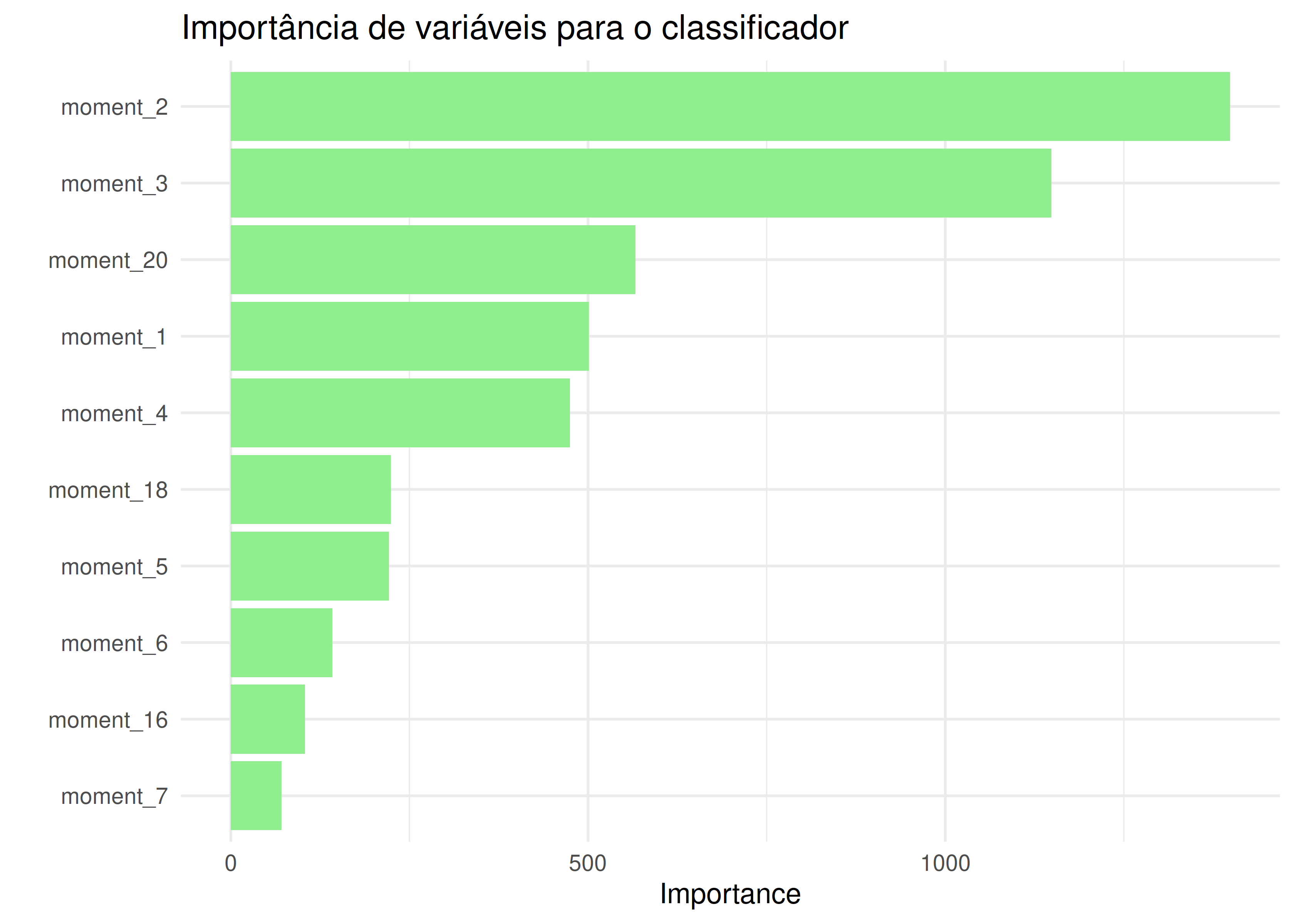

Acho razoável pensar que os momentos mais discriminantes dependem da cesta de distribuições alimentadas. É difícil pensar que assimetria é relevante para distinguir entre uma normal e uma uniforme, por exemplo.

E como ficamos fora da amostra de teste? A função last_fit() pega a receita de dados de treino e aplica na amostra de teste.

workflow_final <- workflow() %>%
  add_recipe(data_rec) %>%
  add_model(modelo_final)

(final_res <- workflow_final %>%
  last_fit(data_split))

## # Resampling results
## # Monte Carlo cross-validation (0.75/0.25) with 1 resamples  
## # A tibble: 1 x 6
##   splits        id          .metrics      .notes      .predictions     .workflow
##   <list>        <chr>       <list>        <list>      <list>           <list>   
## 1 <split [7.5K… train/test… <tibble [2 ×… <tibble [0… <tibble [2,493 … <workflo…

final_res %>%
  collect_metrics()

## # A tibble: 2 x 3
##   .metric  .estimator .estimate
##   <chr>    <chr>          <dbl>
## 1 accuracy multiclass     0.791
## 2 roc_auc  hand_till      0.957

A pergunta era se dá. Até que dá.

Classificando distribuições a partir dos momentos

Pedro Cavalcante

Cuide da saúde, pare de fazer loops

R mais rápido

Jogo da Velha com Q-Learning