Componentes Principais e decomposição de matrizes

Componentes Principais

Eu vou trabalhar no \(\mathbb{R}^2\) pra facilitar. A ideia de encontrar componentes principais é encontrar uma rotação dos dados que resuma melhor a variação deles em menos variáveis. Veja que \(\mathbb{R}^2\) é extremamente infeliz para isso - afinal qual a graça de resumir duas variáveis. Mas a visualização fica bem mais fácil.

Eu vou gerar uma amostra aleatória da normal bivariada, com variância 1, correlação 0.7 e média zero e plottar isso:

library(MASS)
library(ggplot2)

S <- cbind(c(1,.7),c(.7,1))
ams <- mvrnorm(n=100,mu = c(0,0),Sigma=S)
df <- data.frame(ams)
ggplot(df,aes(X1,X2)) + geom_point()

Veja que se eu traçar uma reta na diagonal e uma reta ortogonal a ela, eu vou ter um novo sistema de coordenadas no qual um dos eixos está na direção que tem o máximo de variação:

ggplot(df,aes(X1,X2)) + geom_point() + geom_abline(slope=1,intercept=0)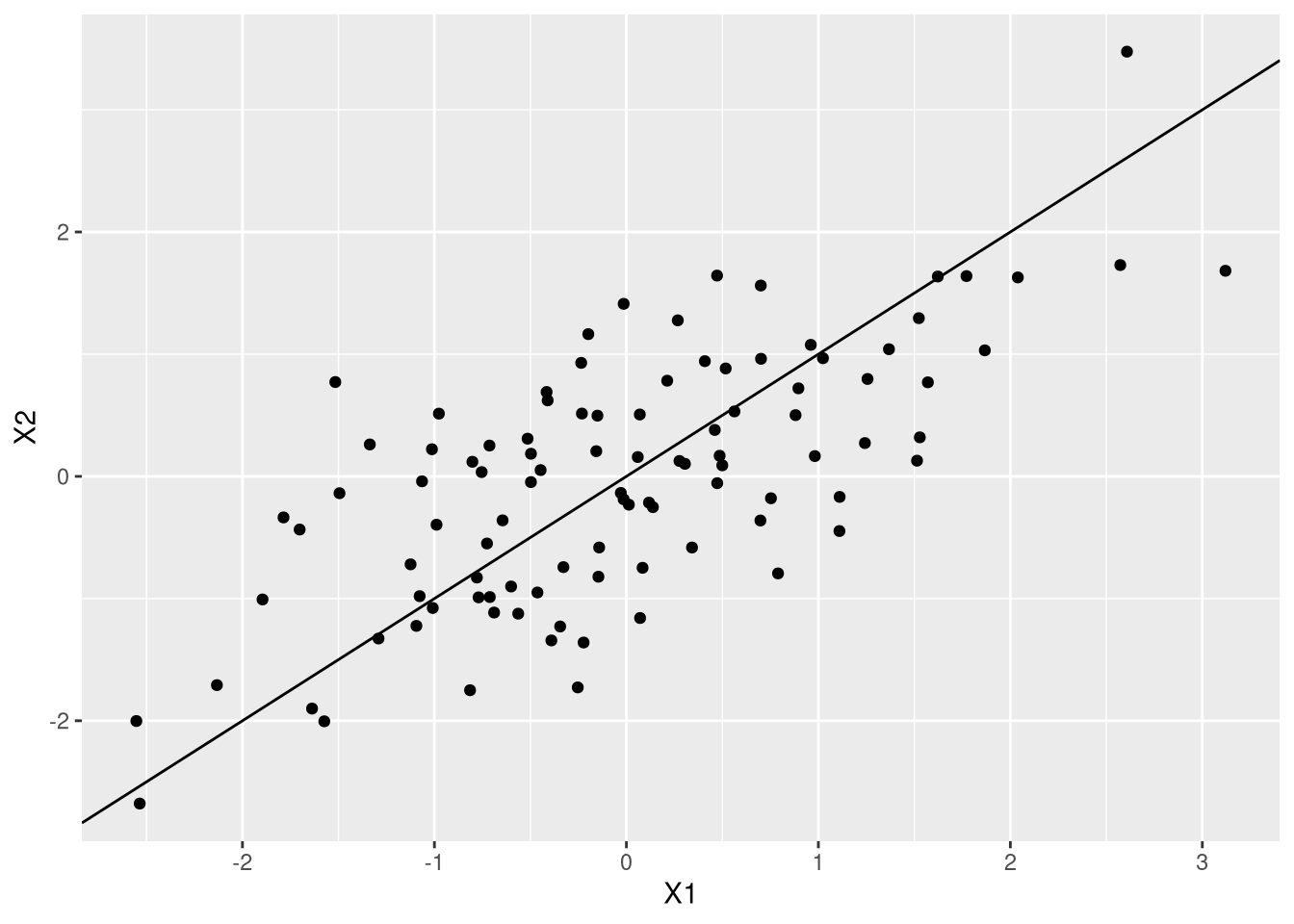

ggplot(df,aes(X1,X2)) + geom_point() + geom_abline(slope=1,intercept=0) + geom_abline(slope=-1,intercept=0)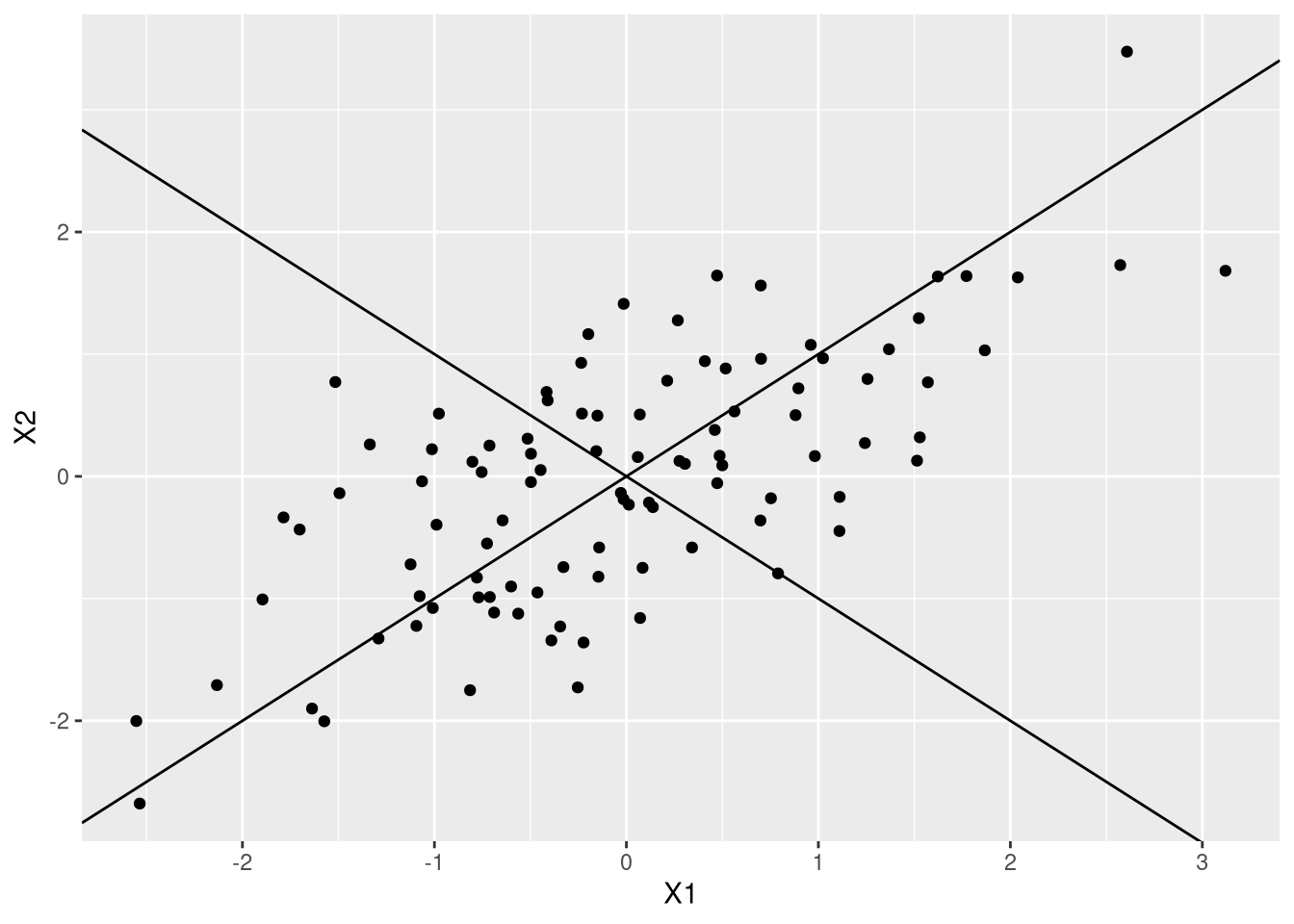

O segundo gráfico só coloca um segundo eixo. Formalizar isso requer o uso de um velho conhecido nosso, os autovalores.

Componentes Principais são autovetores

Como eu quero o máximo de variação, faz sentido começar pensando na matriz de variância, \(\Sigma\). Como \(\Sigma\) é uma matriz simétrica, positiva definida, nós sabemos que os autovetores formam uma base ortogonal e os autovalores são positivos. Eu vou fazer a decomposição em autovalores da matriz de variância, S, e plotar o autovetor associado ao maior autovalor:

auto <- eigen(S)$vectors

ggplot(df,aes(X1,X2)) + geom_point() + geom_segment(x=0,y=0, yend=auto[2,1],xend=auto[1,1],arrow=arrow())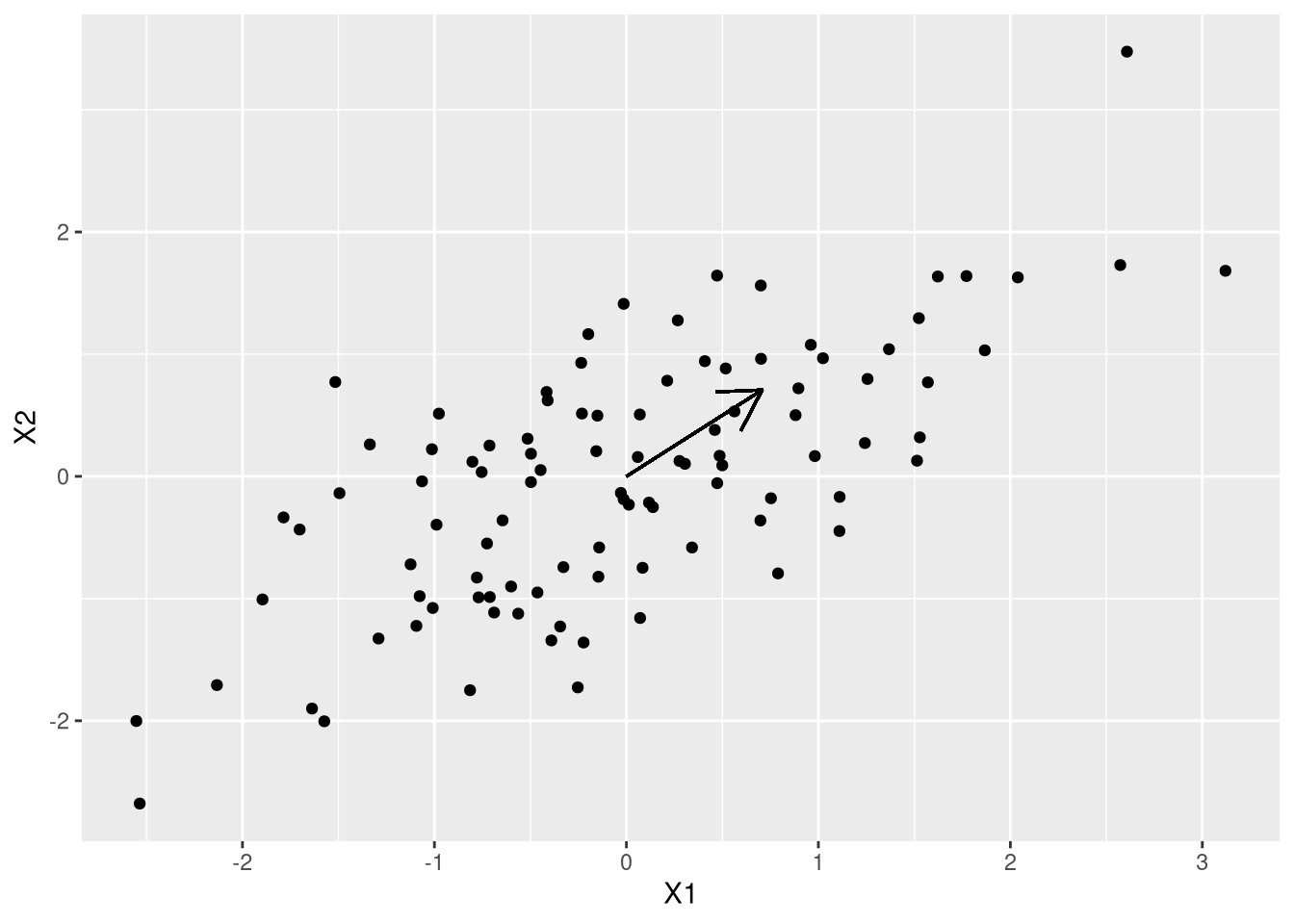

O autovetor aponta exatamente na direção que a gente quer. Vamos entender a matemática: seja \(x\) o vetor de variáveis aleatórias. Nós queremos encontrar um vetor \(\omega\) que faça com que \(\omega^{\prime}x\) gere a maior variância possível, ou seja \(\max_\omega \omega xx^{\prime} \omega^{\prime}\). Veja que sem uma normalização em \(\omega\), qualquer múltiplo vai resolver o problema. Posto de outra forma (100% roubada), se \(\omega\) é um autovetor, então qualquer múltiplo dele também é. Pra facilitar as contas, vamos estabelecer que \(\omega^{\prime}\omega = 1\). Eu poderia resolver usando multiplicador de Lagrange, mas deixa eu fazer algo menos estruturado: comece pela função objetivo do problema de maximização, sabendo que \(xx^{\prime} = \Sigma\):

\[\omega^{\prime} \Sigma \omega\]

Eu já disse que \(\Sigma\) admite uma representação por autovetores que formam uma base ortogonal, então se \(P\) é a matriz de autovetores, e por ser ortogonal, \(P' = P^{-1}\). A matriz de autovalores (que é diagonal) vai ser \(\Lambda\):

\[\omega^{\prime} \Sigma \omega = \omega^{\prime} P^{\prime}\Lambda{}P \omega\]

Agora defina \(\omega{}P = y\) e teremos:

\[\omega^{\prime} \Sigma \omega = \omega^{\prime} P^{\prime}\Lambda{}P \omega = y^{\prime} \Lambda y\]

Claramente, se todos os autovalores fossem substituídos pelo maior autovalor, nós teríamos um número maior (não esqueçam que \(y\Lambda{}y^{\prime} = \sum_{i=1}^{p} y_i^2\lambda_i\)); se substituíssemos todos os autovalores pelo menor autovalor, teríamos um número menor. O maior e o menor autovalor limitam o valor possível de \(y \Lambda y^{\prime}\). Pra facilitar a vida, eu vou considerar os autovalores em ordem decrescente, então \(\lambda_1 > \lambda_2 > ... >\lambda_p\):

\[y\lambda_1y^{\prime} > y \Lambda y^{\prime} > y \lambda_p y^{\prime}\]

Como \(\lambda_1\) e \(\lambda_p\) são escalares:

\[y^{\prime}\lambda_1y = \lambda_1 y^{\prime} y = \lambda_1 \omega^{\prime} P^{\prime} P \omega\]

Na última igualdade eu só substitui a definição de \(y\). Como \(P^{\prime} = P^{-1}\), temos:

\[\lambda_1 \omega^{\prime} P^{\prime} P \omega = \lambda_1 \omega^{\prime} \omega\]

Substituindo no problema original, temos:

\[\lambda_1 \omega^{\prime} \omega \geq \omega^{\prime} \Sigma \omega \geq \lambda_p \omega^{\prime}\omega\]

Agora, \(\omega^{\prime}\omega\) é um escalar, então podemos dividir tudo por essa quantidade e obter:

\[\lambda_1 \geq \frac{\omega^{\prime}\Sigma \omega}{\omega^{\prime} \omega} \geq \lambda_p\]

Impondo a restrição de \(\omega^{\prime}\omega\), nós teremos que:

\[\lambda_1 \geq \omega^{\prime}\Sigma \omega\geq \lambda_p\]

Então a “maior variância possível” é representada pelo maior autovalor e o vetor que realiza a rotação é o autovetor associado.

SVD

A decomposição em valores singulares (Singular Value Decomposition) é outra decomposição bastante importante e famosa, mas nem sempre abordada em cursos de Álgebra Linear. Aplicando em uma matriz qualquer \(A\), que não precisa ser quadrada, o SVD faz:

\[A = USV^{\prime}\]

E \(U\) e \(V\) são matrizes ortogonais (\(U^{\prime} = U^{-1}\) e \(V^{\prime} = V^{-1}\)) e \(S\) é uma matriz diagonal cujo valores são chamados de valores singulares.

Veja que se tivermos trabalhando com \(A^{\prime}A\) - como por exemplo no caso da matriz de covariância \(X^{\prime}X\), então usando o SVD de \(A\) nós podemos reescrever:

\[A^{\prime}A = (USV^{\prime})^{\prime}USV^{\prime} = VSU^{\prime}USV^{\prime} = VS^2V^{\prime}\]

Então veja que os autovalores de \(A^{\prime}A\) são os quadrados dos valores singulares de A e os autovetores são \(V\). Uma relação similar vale para \(AA^{\prime}\).

Como a variância empírica dos dados é calculada com \(X^{\prime}X\), a gente sequer precisa se preocupar em calcular a matriz de variância covariância dos dados, basta passar o SVD na matriz de dados.

Só para dar um exemplo, vamos pegar o famoso mtcars:

data("mtcars")

xx <- cbind(mtcars$mpg,mtcars$cyl,mtcars$disp,mtcars$hp)

Tirando os componentes principais:

comp <- prcomp(xx,scale=T,center=T)

Vamos ver a matriz de rotação:

comp$rotation

##             PC1         PC2        PC3          PC4
## [1,] -0.4963126  0.41505710 -0.7624369 -0.009557844
## [2,]  0.5126614 -0.08416586 -0.3698824 -0.770247652
## [3,]  0.5060829 -0.31928855 -0.5109886  0.617110666
## [4,]  0.4844917  0.84776090  0.1441097  0.160628854

Agora vamos tirar o SVD da matriz e ver a matriz \(V\) da decomposição. Não esqueça que eu preciso centrar e escalarxx (os dados) para ter variância 1 (o que eu vou fazer com o scale):

x_sc <- scale(xx)
svd_x <- svd(x_sc)

svd_x$v

##            [,1]        [,2]       [,3]         [,4]
## [1,] -0.4963126  0.41505710 -0.7624369 -0.009557844
## [2,]  0.5126614 -0.08416586 -0.3698824 -0.770247652
## [3,]  0.5060829 -0.31928855 -0.5109886  0.617110666
## [4,]  0.4844917  0.84776090  0.1441097  0.160628854

Veja que devido a representação do computador de um número real ser finita, as duas representações podiam diferir um pouquinho por erro numérico - isso não acontece justamente porque o prcomp usa svd!

A gente pode fazer a mesma decomposição a partir da matriz de correlação usando os autovalores:

cov_mat <- cor(xx)
eigs <- eigen(cov_mat)

eigs$vectors

##            [,1]        [,2]       [,3]         [,4]
## [1,]  0.4963126  0.41505710  0.7624369 -0.009557844
## [2,] -0.5126614 -0.08416586  0.3698824 -0.770247652
## [3,] -0.5060829 -0.31928855  0.5109886  0.617110666
## [4,] -0.4844917  0.84776090 -0.1441097  0.160628854

Veja que a diferença entre esses valores e a matriz v é que eles são multiplicados por -1

Muito conveniente quando a computação e a matemática concordam.