Componentes Principais e Variáveis Instrumentais
Eu já falei de variáveis instrumentais e de componentes principais. Eu nunca misturei os dois, apesar da ideia deste post ter me ocorrido a muito tempo.
Eu já falei como muitos instrumentos causam viés e como componentes principais podem ser usados para resumir muitas variáveis. Naturalmente, alguém poderia se perguntar se a gente poderia passar componentes principais em um conjunto de instrumentos e usar apenas alguns poucos instrumentos que resumem a maior parte da variabilidade dos dados.
Vamos fazer um pequeno exemplo com 100 observações e cinquenta variáveis instrumentais. As variáveis instrumentais são z e a variável omitida vai ser u:
set.seed(181121)
library(AER)
n <- 100
q <- 50
z <- matrix(rnorm(n*q),ncol=q)
u <- rnorm(n)Os coeficientes do instrumento são aleatórios mas relativamente baixos. Isso faz com que os instrumentos expliquem muito da variação, mas cada instrumento explica muito pouco da variação pra ser usado como um instrumento sozinho:
cofs <- runif(q,-0.8,0.8)Eu vou criar as variáveis x e y que são o regressor e a variável dependente, respectivamente:
x <- 0.1 + z%*%cofs + u + rnorm(n)
y <- 1.5*x + 2*u + rnorm(n)Veja que o coeficiente da variável \(x\) é 1.5. Eu vou iniciar estimando por Mínimos Quadrados, por Variável Instrumental usando os 50 instrumentos, e por variável instrumental usando o primeiro instrumento - não há nada de especial no primeiro instrumento, eu poderia ter escolhido aleatoriamente um instrumento:
mqo <- lm(y ~ x)
iv <- ivreg(y ~ x|z)
iv1 <- ivreg(y ~ x|z[,1])Agora eu vou usar o prcomp para estimar os componentes principais de \(z\). A variável q_prime me diz quantos componentes principais eu vou usar (10):
q_prime <- 10
new_z <- prcomp(z,center = TRUE,scale. = TRUE)
new_z <- new_z$x[,1:q_prime]
iv_pr <- ivreg(y ~ x|new_z)Vamos ver os resultados:
tabela <- c(coef(mqo)[2],coef(iv)[2],coef(iv1)[2],coef(iv_pr)[2])
names(tabela) <- c("MQO","IV-Todos","IV-1º Instrumento","IV-Componentes Principais")
knitr::kable(tabela,col.names =" ")| MQO | 1.734031 |
| IV-Todos | 1.681225 |
| IV-1º Instrumento | 2.144132 |
| IV-Componentes Principais | 1.620479 |
Isso sugere que a gente está em um bom caminho. Mas, uma única simulação não adianta de muita coisa, então vamos amarrar o código acima em uma função e fazer umas mil repetições. Eu vou permitir alterar o tamanho da amostra, o número de instrumentos, o número de fatores usados e o coeficiente do instrumento em relação a variável x:
library(purrr)
library(ggplot2)
library(tidyr)uma_simul <- function(n,q,q_prime,coef_prim = 0.8){
z <- matrix(rnorm(n*q),ncol=q)
u <- rnorm(n)
cofs <- runif(q,-coef_prim,coef_prim)
x <- 0.1 + z%*%cofs + u + rnorm(n)
y <- 1.5*x + 2*u + rnorm(n)
mqo <- lm(y ~ x)
iv <- ivreg(y ~ x|z)
new_z <- prcomp(z,center = TRUE,scale. = TRUE)
new_z <- new_z$x[,1:q_prime]
iv_pr <- ivreg(y ~ x|new_z)
iv1 <- ivreg(y ~ x|z[,1])
return(c(coef(mqo)[2],coef(iv)[2],coef(iv1)[2],coef(iv_pr)[2]))
}
input <- replicate(1000,100,simplify = FALSE)
output <- map(input, uma_simul, q = 50,q_prime = 10)
output <- do.call(rbind,output)
colnames(output) <- c("MQO","IV-Todos","IV-1º Instrumento","IV-Componentes Principais")
knitr::kable(colMeans(output),col.names =" ")| MQO | 1.6588926 |
| IV-Todos | 1.5852560 |
| IV-1º Instrumento | 0.0834184 |
| IV-Componentes Principais | 1.5425258 |
O IV com um único instrumento sofreu um sério problema nessa simulação. O IV com 10 componentes principais é só marginalmente melhor que todos os instrumentos. Vamos olhar a distribuição de cada estimador usando o ggplot, e isso vai exigir arrumar os dados usando o tidyr. A gente vai colocar uma linha vertical no valor verdadeiro do coeficiente:
output_tidy <- pivot_longer(as.data.frame(output),cols = everything(), names_to = "Estimador", values_to = "Valor")
ggplot(output_tidy,aes(Valor)) + geom_histogram() + facet_wrap(vars(Estimador),scales = "free")+ geom_vline(aes(xintercept = 1.5)) + theme_minimal()## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.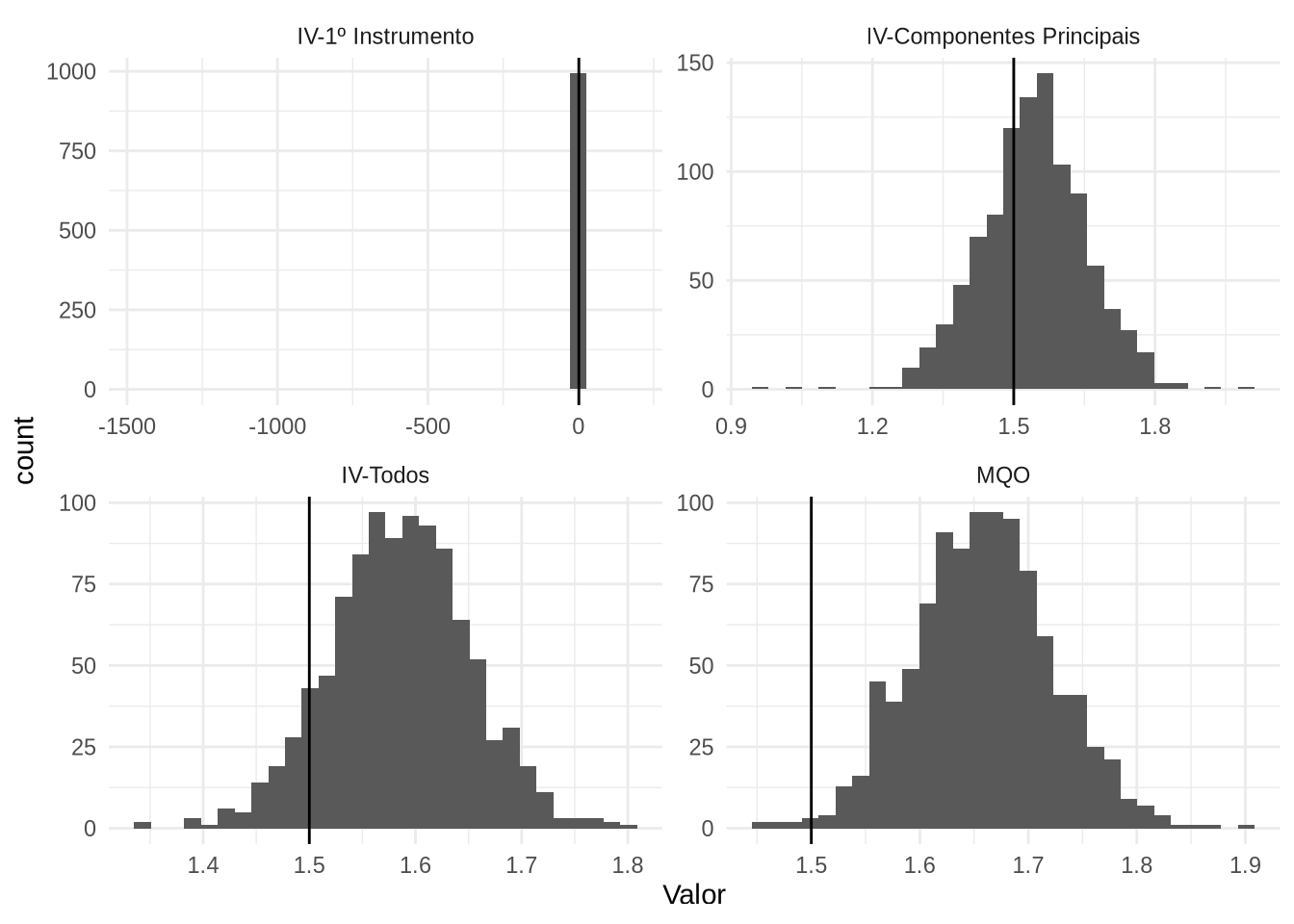
Vamos realmente aloprar e criar um exemplo com 90 instrumentos. Dessa vez, eu vou usar apenas um componente principal:
input <- replicate(1000,100,simplify = FALSE)
output <- map(input, uma_simul, q = 90,q_prime = 10,coef_prim = 0.1)
output <- do.call(rbind,output)
colnames(output) <- c("MQO","IV-Todos","IV-1º Instrumento","IV-Componentes Principais")
knitr::kable(colMeans(output),col.names =" ")| MQO | 2.367137 |
| IV-Todos | 2.355675 |
| IV-1º Instrumento | 3.644071 |
| IV-Componentes Principais | 2.169526 |
Vamos fazer o histograma das estimações:
output_tidy <- pivot_longer(as.data.frame(output),cols = everything(), names_to = "Estimador", values_to = "Valor")
ggplot(output_tidy,aes(Valor)) + geom_histogram() + facet_wrap(vars(Estimador),scales = "free") + geom_vline(aes(xintercept =1.5)) + theme_minimal()## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.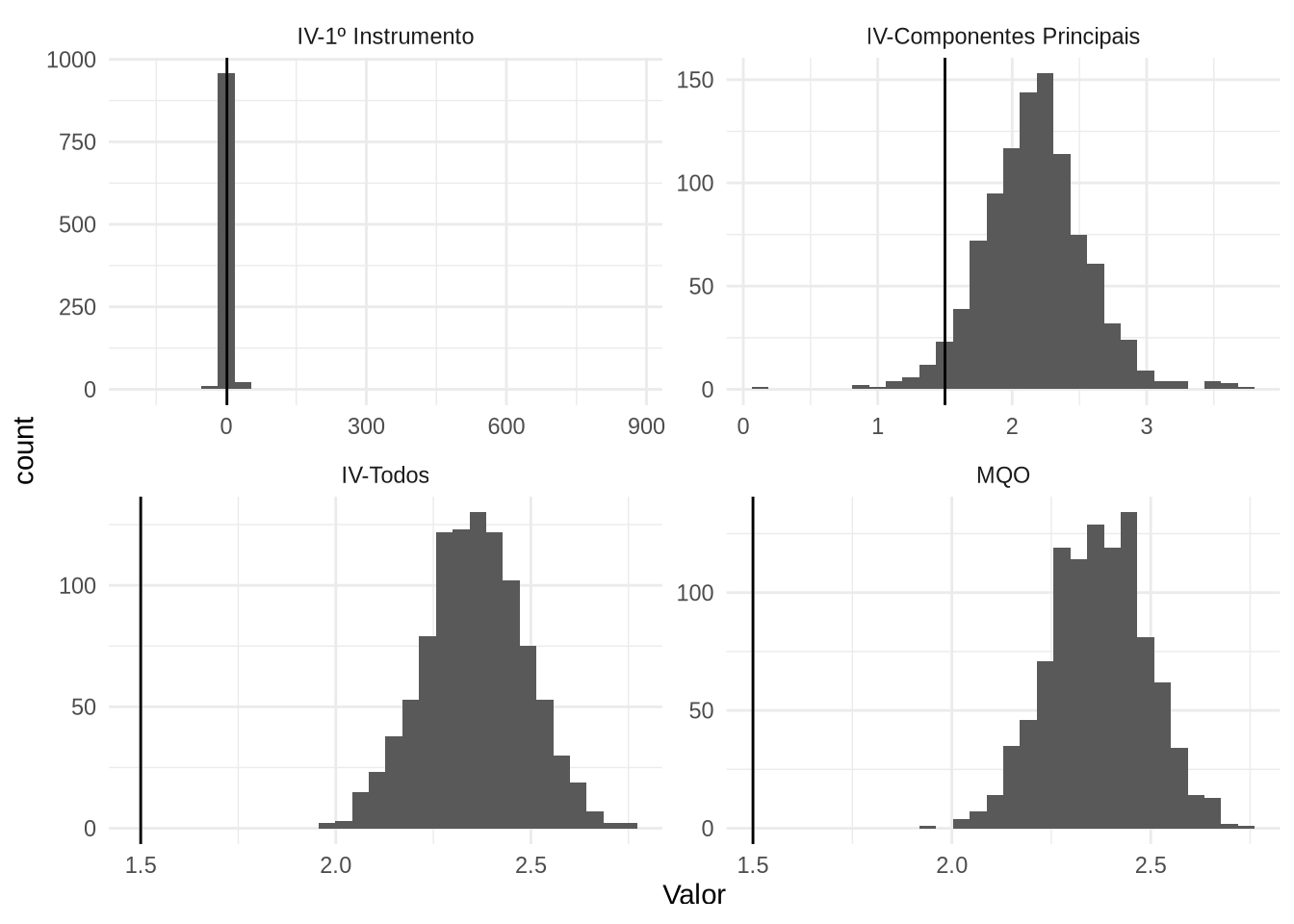 As distribuições de um instrumento é incrivelmente mal comportada e a distribuição usando componentes principais tem distribuição bem menos concentrada que Mínimos Quadrados ou usando todos os instrumentos.
As distribuições de um instrumento é incrivelmente mal comportada e a distribuição usando componentes principais tem distribuição bem menos concentrada que Mínimos Quadrados ou usando todos os instrumentos.
Nós podemos brincar um pouquinho e reduzir a quantidade de componentes principais. Vamos testar dois:
input <- replicate(1000,100,simplify = FALSE)
output <- map(input, uma_simul, q = 90,q_prime = 5,coef_prim = 0.1)
output <- do.call(rbind,output)
colnames(output) <- c("MQO","IV-Todos","IV-1º Instrumento","IV-Componentes Principais")
knitr::kable(colMeans(output),col.names =" ")| MQO | 2.371017 |
| IV-Todos | 2.360232 |
| IV-1º Instrumento | 2.076244 |
| IV-Componentes Principais | 2.165709 |
output_tidy <- pivot_longer(as.data.frame(output),cols = everything(), names_to = "Estimador", values_to = "Valor")
ggplot(output_tidy,aes(Valor)) + geom_histogram() + facet_wrap(vars(Estimador),scales = "free") + geom_vline(aes(xintercept =1.5)) + theme_minimal()## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.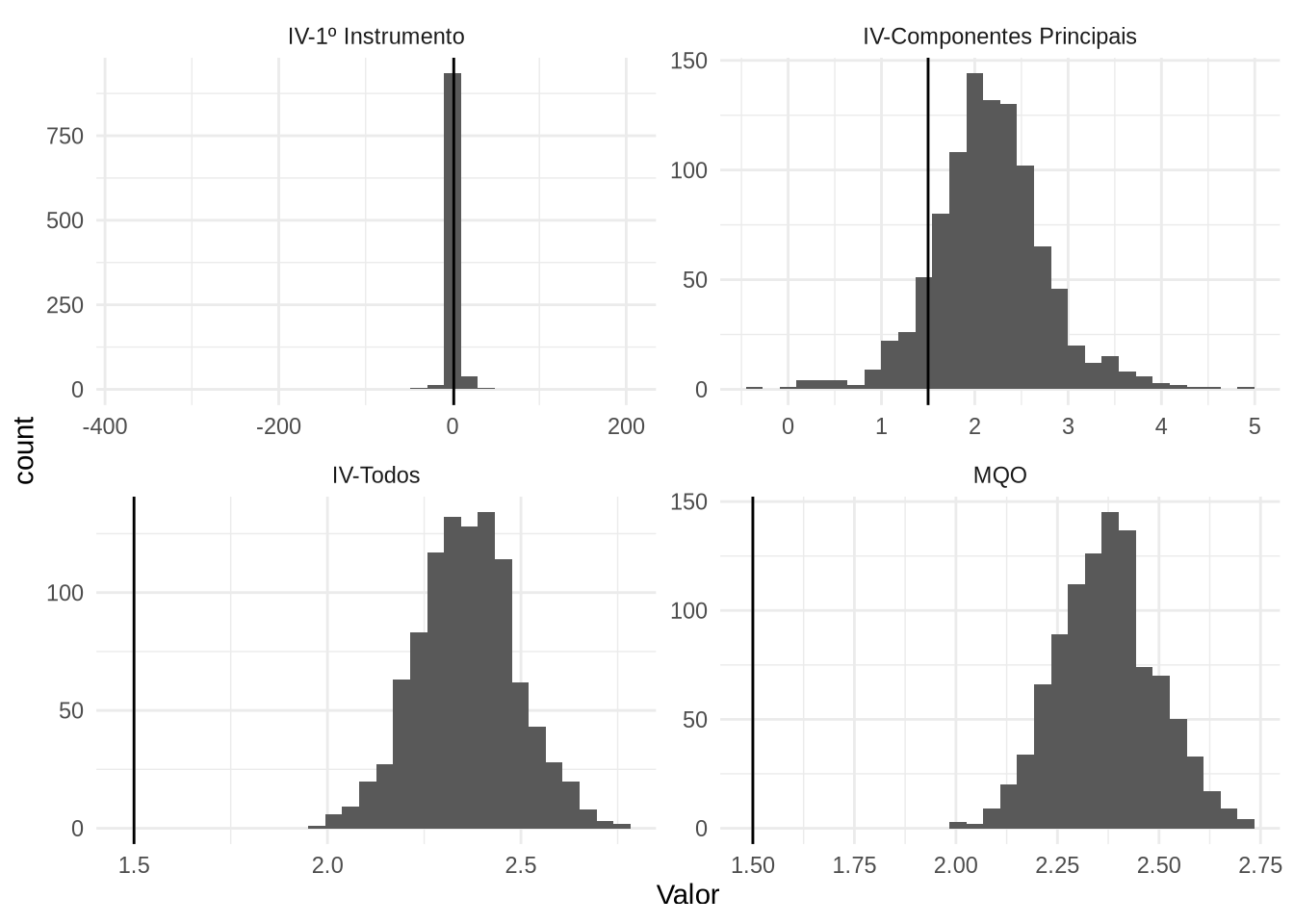
Diminuir o número de componentes parece ser uma faca de dois gumes: o viés cai, mas a variância aumenta.
Essas simulações mostram que usar IV pode gerar tanto viés quanto MQO, mas este post já tá grande demais.