Crescimento Exponencial, mas sem o Corona

Uma família de funções que aparece em variados contextos é a exponencial:

\[f(x) = ab^x\]

Se diferenciarmos em particular a função \(b^x\) vamos ter \(b^x \log_e b\). Se \(b>1\) a função cresce, se for menor, decresce. A constante \(e\) é a única que equaliza a função e a derivada.

Não queria me alongar muito nem falar de corona então vou só fazer um gráfico bonito mostrando como a função muda a depender de qual \(b\) passamos como base. O exercício é interessante porque explora algumas ferramentas muito úteis do {tidyverse}.

library(tidyverse)
library(gganimate)

expfoo <- function(base) { # uma fábrica de funções
  
 function(x) { base^x }
  
}

(sim <- tibble(A = seq(0.1, 10, 0.05)) %>%
  mutate(foo = map(A, ~ expfoo(.x)), # geramos uma lista de funções
         y = map(foo, ~ .x(seq(-1, 1, .1))), # geramos uma lista aplicando as funções
         x = rep(list(seq(-1, 1, .1)), nrow(.))) %>% 
  select(A, x, y) %>%
  unnest(c(x,y)))

## # A tibble: 4,179 x 3
##        A      x     y
##    <dbl>  <dbl> <dbl>
##  1   0.1 -1     10   
##  2   0.1 -0.9    7.94
##  3   0.1 -0.8    6.31
##  4   0.1 -0.7    5.01
##  5   0.1 -0.6    3.98
##  6   0.1 -0.5    3.16
##  7   0.1 -0.400  2.51
##  8   0.1 -0.300  2.00
##  9   0.1 -0.200  1.58
## 10   0.1 -0.100  1.26
## # … with 4,169 more rows

sim %>%
  ggplot(aes(x = x, y = y, color = A, group = A)) +
  geom_line() +
  geom_vline(xintercept = 0) +
  geom_hline(yintercept = 0) +
  scale_color_gradient(low = "#d12e2e", high = "#1e6cd9") +
  ylim(-1, 6) +
  theme_minimal() +
  labs(title = "A família exponencial")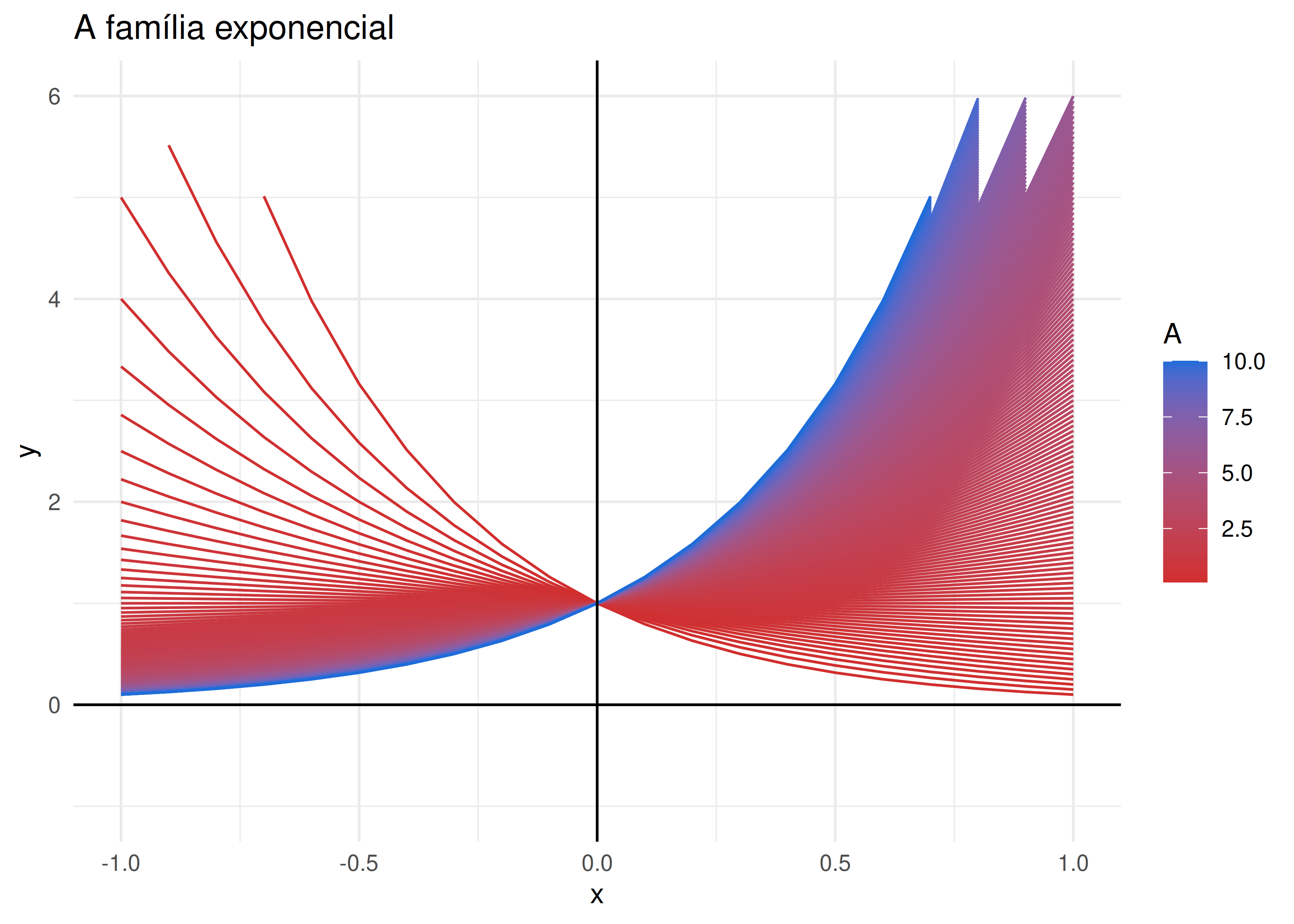

animacao <- sim %>%
  ggplot(aes(x = x, y = y, color = A, group = A)) +
  geom_line() +
  geom_vline(xintercept = 0) +
  geom_hline(yintercept = 0) +
  scale_color_gradient(low = "red", high = "green") +
  ylim(-1, 5) +
  theme_minimal() +
  transition_reveal(A) +
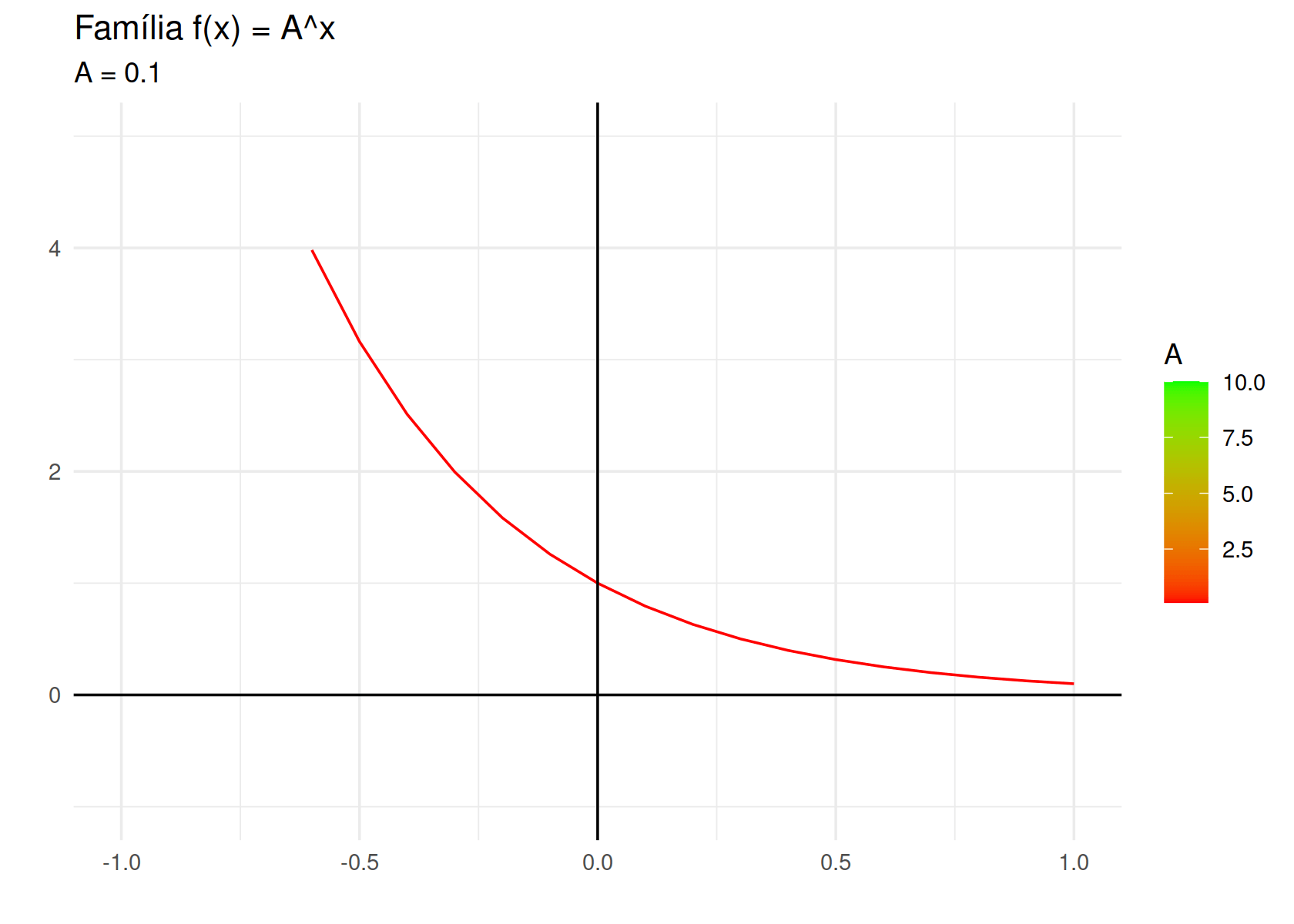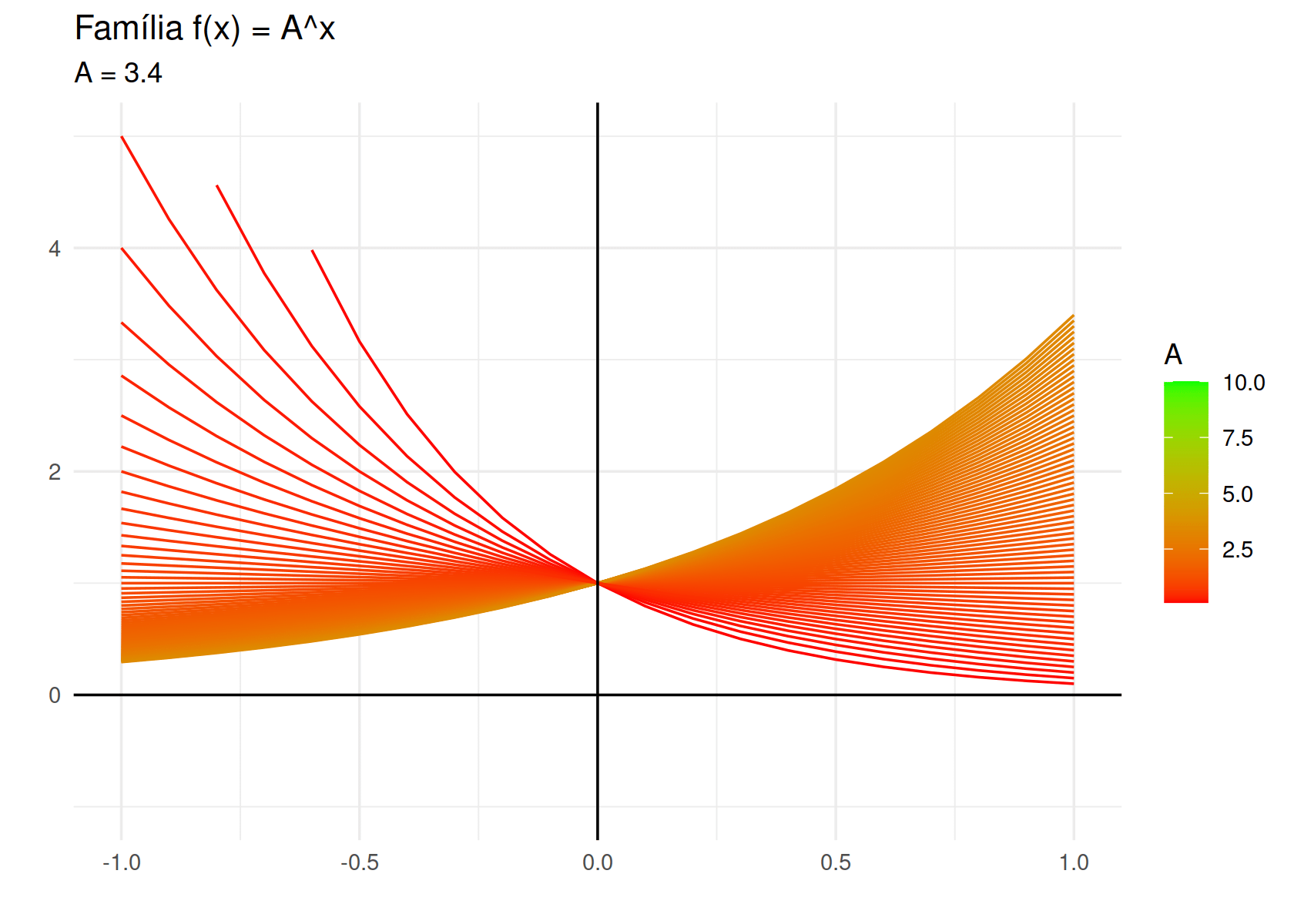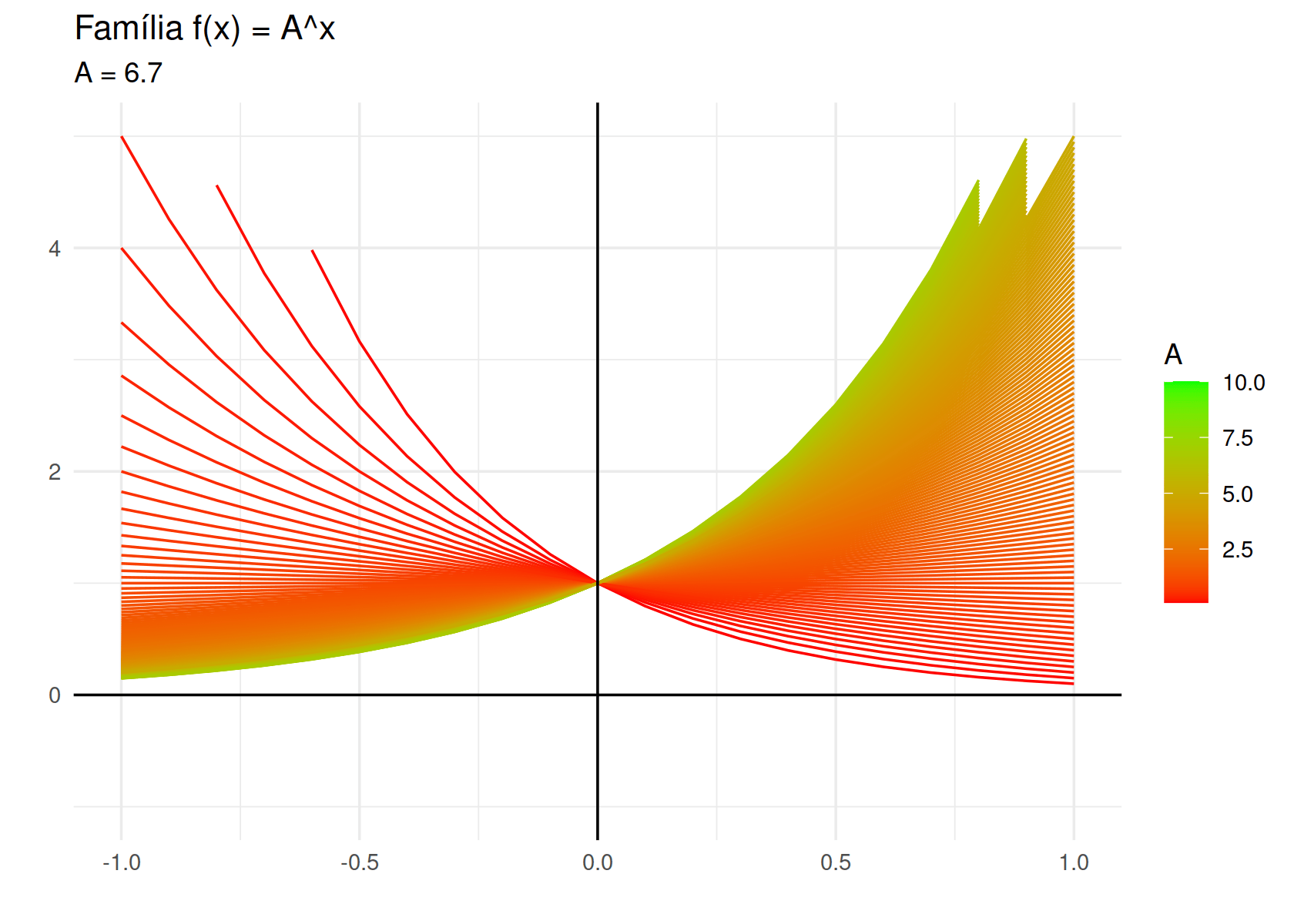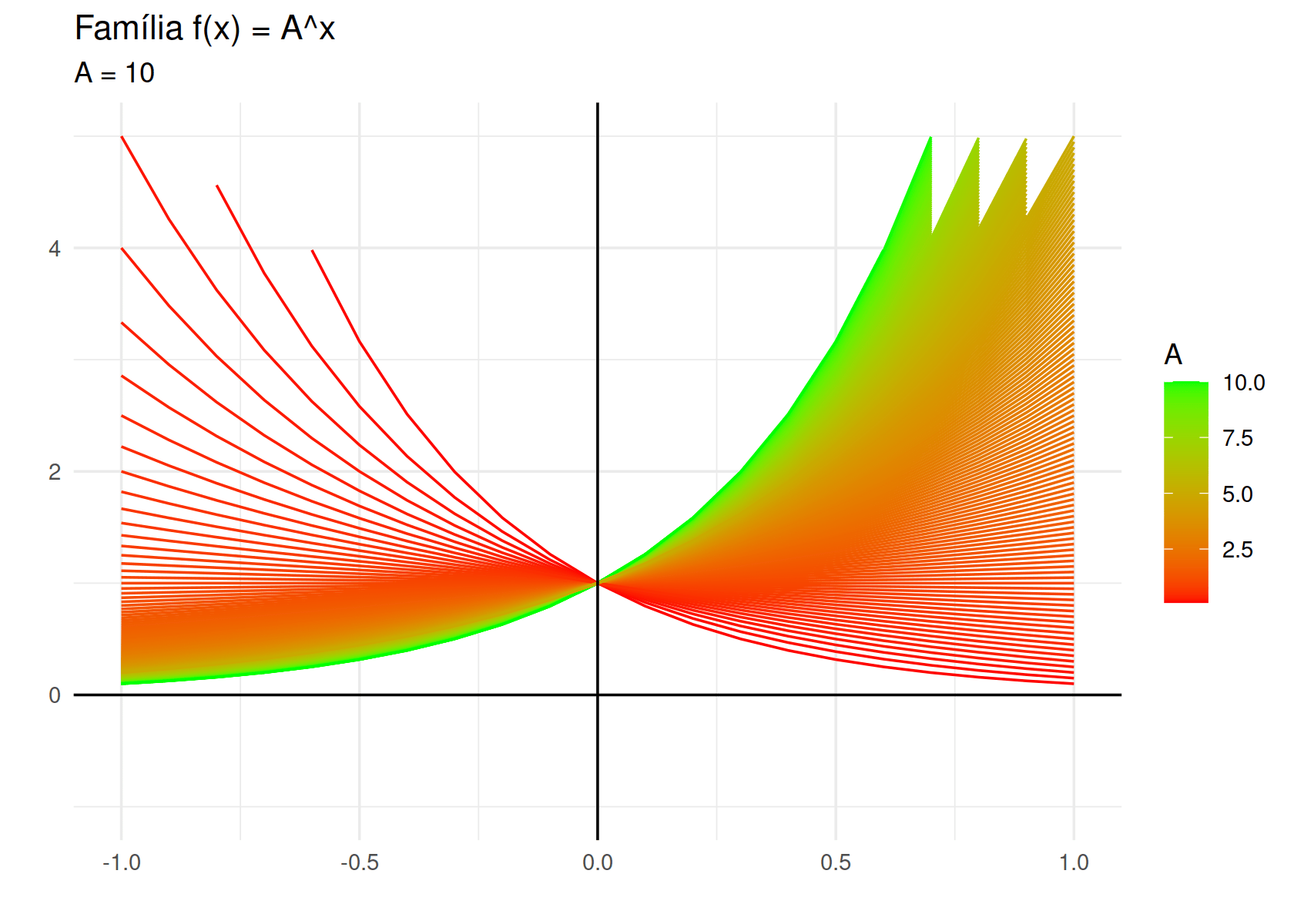
  labs(title = "Família f(x) = A^x",
         subtitle = "A = {round(frame_along, 3)}",
         x = "",
         y = "")

animate(animacao)